
What is Sampling?
According to the Centre of Economics and Business Research, people in the UK drank 95 million cups of coffee in 2018. The astounding thing about this figure is, at first, the sheer amount of caffeinated beverages being consumed every year. The second thing you might gawk at: how in the world do they arrive at such a number?
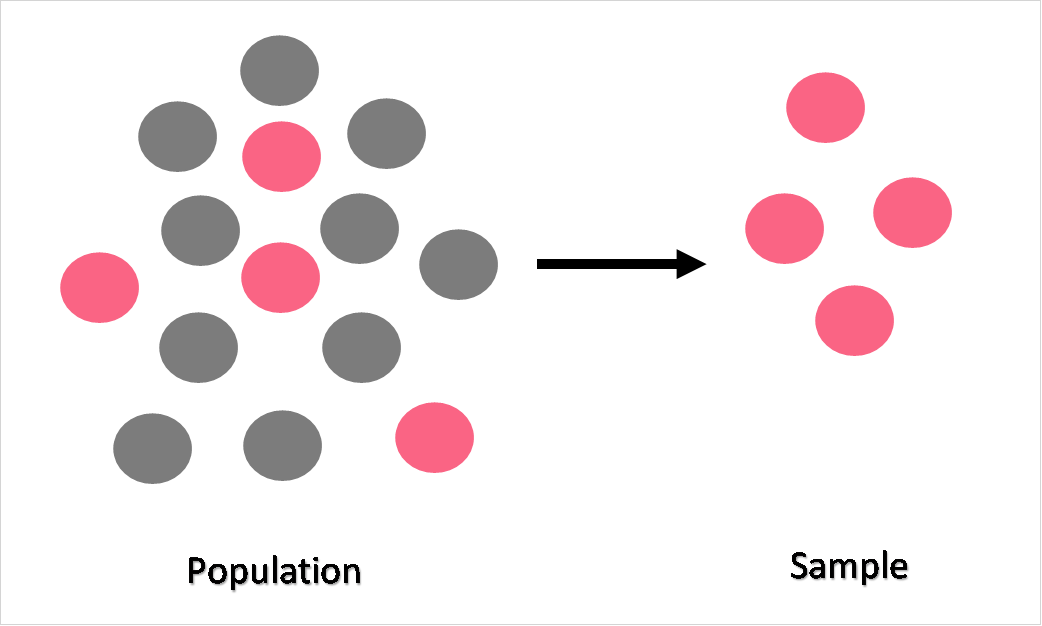
While facts like these are often presented to us as objective, solid truths - I’d like to invite you for a moment to think about the process behind the number. It would be impossible for the CEBR, or anyone for that matter, to ask all of the 67 million individuals living in the UK about their coffee consumption. The population in statistics is defined as the entire group of people, things or ideas you want to draw a conclusion from. In this case, it would be all coffee drinkers living in the UK.
This is where a sample comes in, which is a group within a population that you will collect data from. In this example, the CEBR surveyed 2,000 adults in the UK to estimate the cups of coffee made in 2018.
When is Sampling Used?
Sampling is used when you cannot collect data from everyone in your defined population - which occurs the majority of times. As mentioned above, estimating statistics from a population involves a process, which is known as methodology.
Methodology is a set of methods used in a particular activity. Sampling methodology is the system of methods used to sample from a population. Sampling methodology belongs to the vital branch of statistics that covers statistical methodology. All instances of research or studies that collect data have to carefully lay out exactly how they will select a sample that is representative, or one that accurately reflects characteristics in the population.
Types of Sampling
While there are many sampling methods, each one falls under either one of the following categories.
| Probability sampling | Sample has random selection |
| Non-probability sampling | Sample has non-random selection |
As seen in the table above, probability sampling is when a sample has random selection. Because the selection is random, this means that every member of the population has a chance at being picked. Four common probability samples are summarized in the table below.
| Simple Random Sample (SRS) | Every member of the population has an equal chance of selection. Randomly selected based on random process. |
| Systematic Sample | Every member of the population is selected based on regular intervals |
| Stratified Sample | The population is divided into groups (strata) based on a similar characteristic. Based on proportions of the population for the given characteristic, you sample from each strata using SRS or systematic sampling. |
| Cluster Sample | The population is divided into groups (clusters), however they are sampled based on entire clusters, as opposed to sampling from within the group. |
Take a look at the images below, which should help you get a better idea of the differences between each of these four basic probability samples.
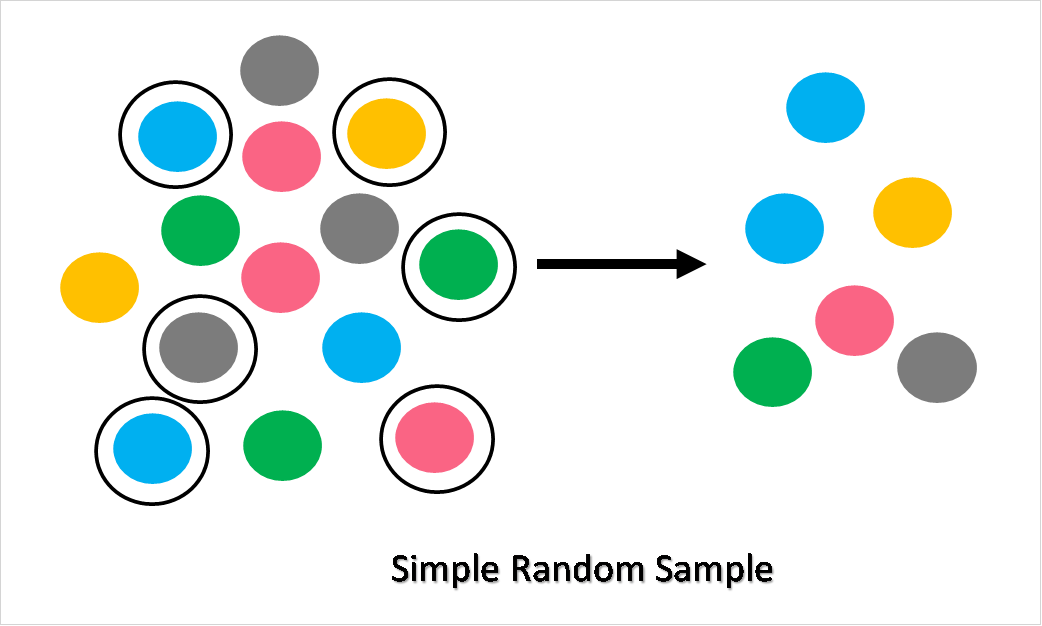

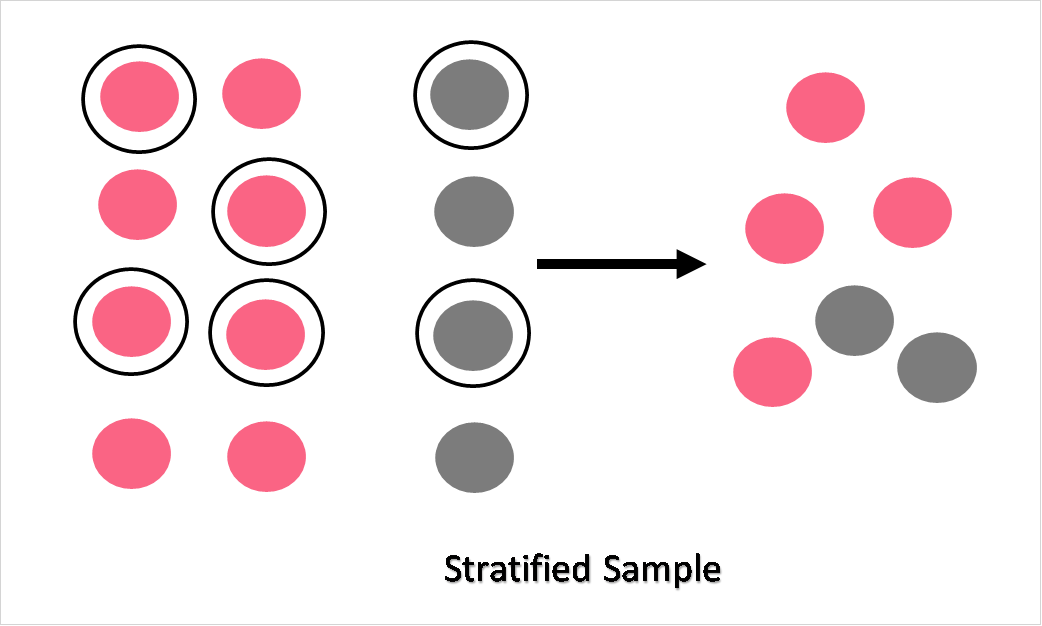
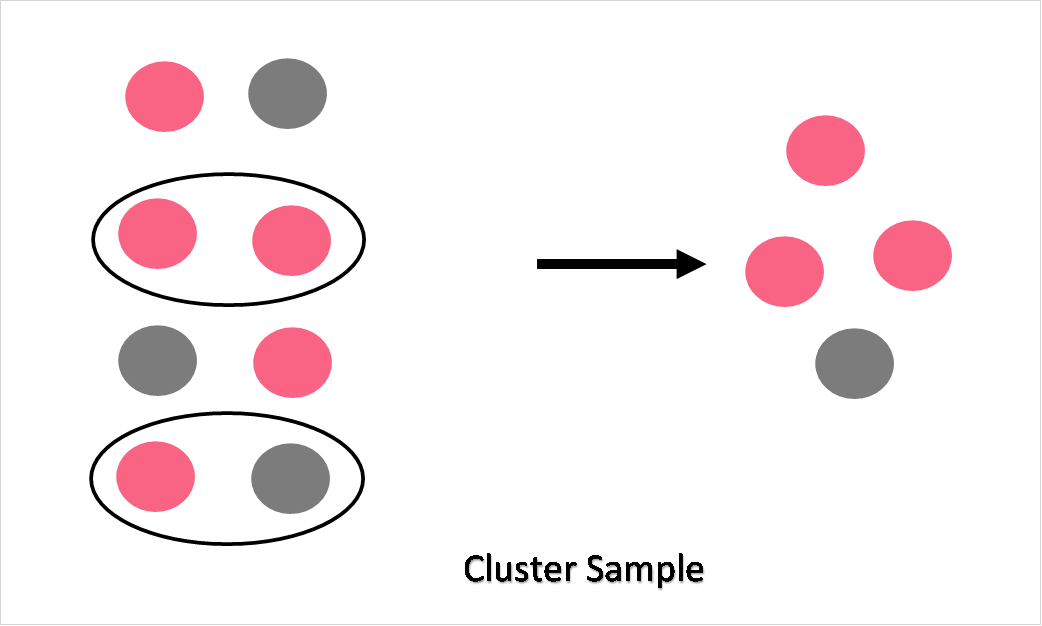
Non-probability sampling, on the other hand, has non-random selection. Because the selection is not random, this means that not every member of the population has a chance at being picked. Four common non-probability sampling methods are summarized with their definitions in the table below.
| Convenience Sample | This is the most common sample people think of when they think of surveys. These samples are picked based on convenience, such as proximity or accessibility. |
| Voluntary Response Sample | This is the second most common sample people tend to think of when thinking about surveys. These involve sending out surveys and forming your sample based on who responded. |
| Purposive or Judgement Sample | These samples involve using an expert opinion or research in order to select a sample. This is most often used in qualitative research. |
| Quota Sample | These samples are drawn based on a certain quota. Interviewers are often given a specific quota of subjects they should attempt to complete surveys with. |
Of course, it is often easier to visualize sampling methods. Take a look at the visual representations of each method below in order to get a better grasp of what each sampling method looks like.
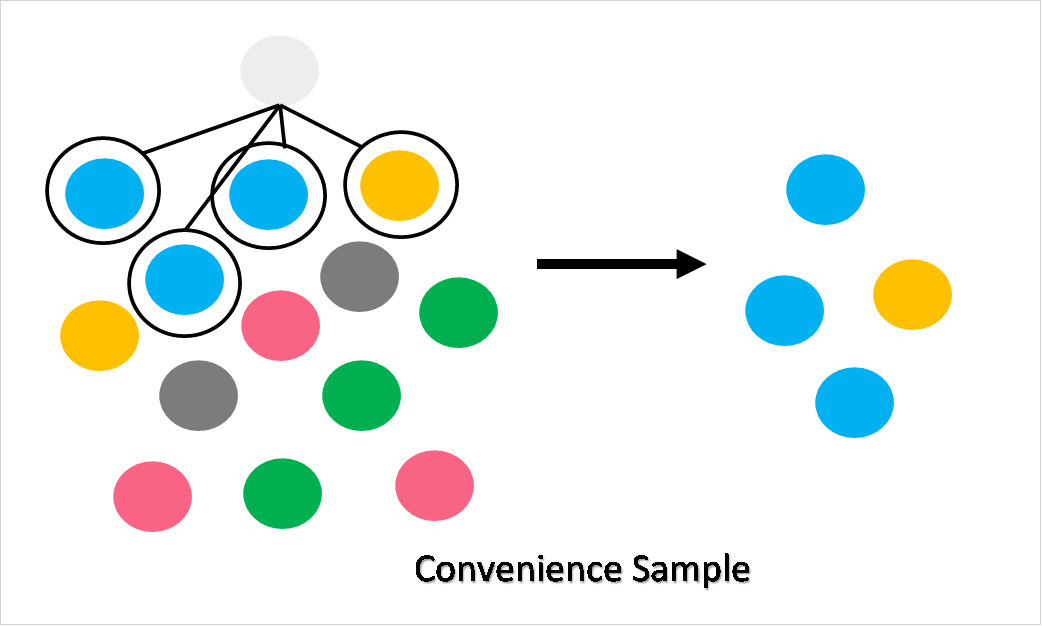


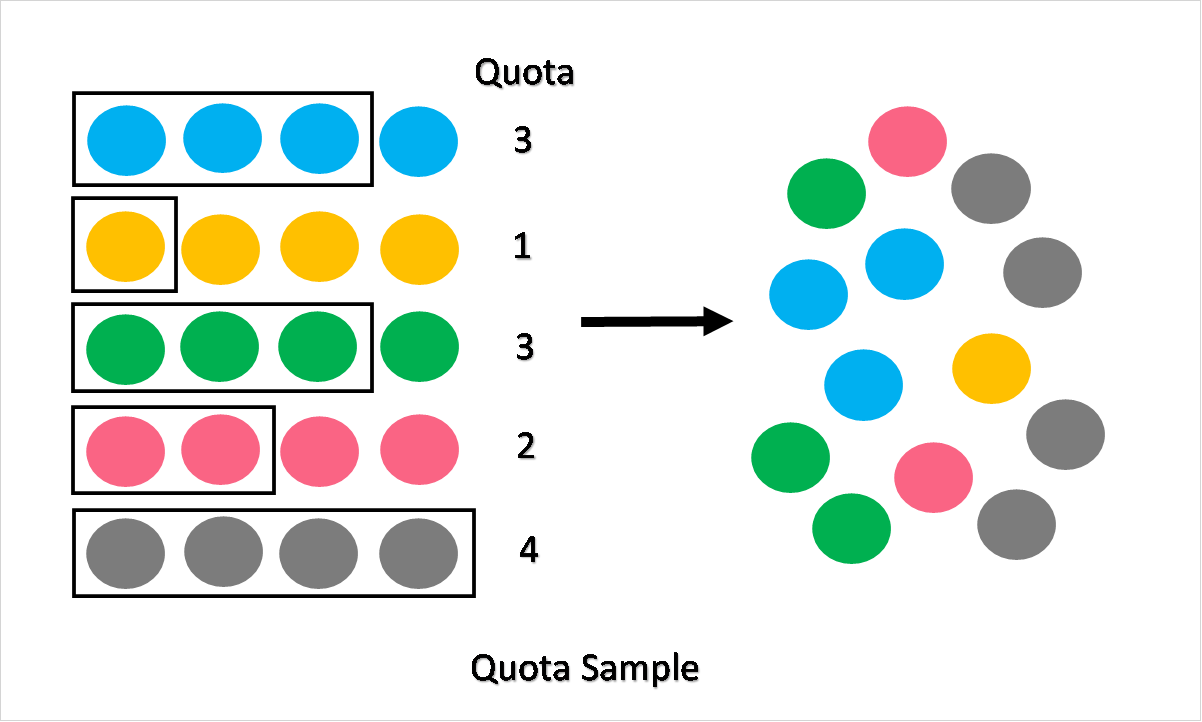
There are many different reasons why researchers may choose either of the two methods. The top two reasons are: cost and time. Even when a researcher knows that a certain method will lead to more accuracy, it may be that the method is simply cost or time-ineffective. Below, we go over when it is more advantageous to use probability sampling and when to use non-probability sampling.
| Probability Sampling | Used when you have a complete population list to choose from. This is because you can ensure that all participants have an equal chance of being selected. |
| Non-probability Sampling | Used when there is no complete population list or when a specific population needs to be studied. As mentioned before, it is also often used in qualitative research. |
Let’s take a look at some concrete examples using three types of probability and non-probability samples. The table below summarizes each example and why each sampling method is used.
| Population | Sample | Example |
| All of a company’s employees | Stratified Sample | The company has 300 female employees and 500 male employees. Gender will be our strata, so we divide the company by gender and select 30 females and 50 males through an SRS, which is a representative sample. |
| All of a company’s employees | Cluster Sample | The company operates in 10 different countries around the world. You select 5 offices out of these 10 through random sampling. While it can be hard to get a representative sample through this method, it's great when large populations are involved. |
| All of a company’s employees | Voluntary Sample | The company sends out a company wide email and while the majority don’t fill in the survey, there are about 100 that do. This is convenient, but can be biased. |
As mentioned, there are many advantages and disadvantages to using one sampling method over another. Below, you’ll find some of the common advantages and disadvantages of probability samples.
| Pro | Con | |
| Simple Random Sample (SRS) | Can generalize to the population | Can be expensive or time consuming. Many don’t have a list of the whole population. |
| Systematic Sample | Can be easier than SRS while still being random | Can have a skewed sample if there is a hidden pattern in the population list |
| Stratified Sample | Great if you want to ensure sample is proportionate to the population | Can be expensive or time consuming |
| Cluster Sample | Great if you have a population that is widely spread out or very large | If there is a major difference between clusters it can lead to errors |
When it comes to non-probability sampling, there are also pros and cons to take into account. Check out some of the ones summarized below.
| Pro | Con | |
| Convenience Sample | Very inexpensive and not time consuming | Cannot really generalize to the population. Not really any way to tell if the sample is representative. |
| Voluntary Response Sample | Very inexpensive and not time consuming | Cannot really generalize to the population. Always some level of bias as those willing to respond more likely to have stronger opinions. |
| Purposive or Judgement Sample | Great if you want to perform some qualitative research | Can be done wrong if not handled correctly. Can be expensive and time consuming. |
| Quota Sample | Can get a better degree of representativeness if you’re unable to do a probability sample | Can be biased because quota is filled based on accessibility or convenience |













