Chapters
In previous sections, you learned the basics of standard deviation, including how to calculate it and how it compares to other measures of variability, such as variance. Here, you’ll learn more in-depth about standard deviation, some of its characteristics and how you can interpret the measure.

What is Standard Deviation?
To recap, the standard deviation is a measure of variability in descriptive statistics. This means that it is used to measure how much the observations within a data set vary from each other. In general, interpreting the standard deviation follows these rules of thumb:
- The lower the standard deviation, the closer the values are to the mean and the less variability there is
- The higher the standard deviation, the farther the values are spread from the mean and the more variability there is
How to Calculate Standard Deviation
Recall that the formula for the standard deviation is different for the population and sample. Another way to write standard deviation is to simply write “SD.” A shortcut to calculating standard deviation is to use the variance. The variance is another measure of variability and is the square of the standard deviation.
If you are in a situation where you’re only provided the variance, but want to know the standard deviation, simply take the square root of the variance. This is easy to remember because of the notation used for both measures. In the table below, you’ll find the notation and formulas for each.
| Population | Sample | |
| Standard Deviation Notation | \[ \sigma \] | \[ s \] |
| SD Formula | \[ \sigma = \sqrt{ \frac{\Sigma(x_i - \mu)^2}{N} } \] | \[ s = \sqrt{ \frac{\Sigma(x_i - \bar{x})^2}{n-1} } \] |
| Variance Notation | \[ \sigma^2 \] | \[ s^2 \] |
| Variance Formula | \[ \sigma = \ \frac{\Sigma(X - \mu)^2}{N} \] | \[ s^2 = \frac{{\sum_{n}^{i=1}{ {(X_{i}}-{X_{avg}})^2}}}{n-1} \] |
How to Calculate the Standard Deviation for Grouped Data
Often, people may choose to group their data in order to display or analyse their data set more efficiently. For example, taking a quantitative variable like age and transforming it into categorical age groups or taking a quantitative variable like points on a test and transforming them into categorical grade groups.
This might be easier to visualize, so let’s take the second example. In the table below are test scores from a classroom.
| Test Score Categories | Frequency 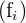 |
| 10 - 20 | 1 |
| 20 - 30 | 8 |
| 30 - 40 | 5 |
| 40 - 50 | 9 |
| 50 - 60 | 8 |
| 60 - 70 | 10 |
| 70 - 80 | 75 |
| Total | 115 |
We want to know the standard deviation, however, we don’t have information on the individual test scores of each of the 115 students. In order to calculate group standard deviation, we have modify the standard deviation formula just a bit. While the formula for grouped standard deviation is different for the population and sample, we’ll focus only on sample grouped SD here. The formula looks like:
\[
s_{grouped} = \sqrt{ \frac{\Sigma f(x_{m} - \bar{x})^2}{n-1} }
\]
While this might look complicated, it is quite simple. Below, you’ll find the interpretation of each step in the formula.
| Step | Formula |
| 1.Find the midpoint values of the groups | \[x_m= \dfrac{(upper \thickspace bound - \lower \thickspace bound)}{2}\] |
| 2.Multiply these midpoint values by the frequency | \[x_{m}*f_{i}\] |
| 3.Add these multiplied values and divide by the sample size to get the grouped mean | \[ \bar{x}= \dfrac{\Sigma(x_{m}*f_{i})}{n} \] |
| 4.Subtract the grouped mean from the midpoint values | \[x_{m}-\bar{x}\] |
| 5. Square these subtracted values | \[(x_{m}-\bar{x})^2\] |
| 6. Multiply the frequency by these squared values | \[f_{i}*(x_{m}-\bar{x})^2\] |
| 7. Add all the multiplied values | \[\Sigma f_{i}*(x_{m}-\bar{x})^2\] |
| 8. Divide these summed values by the sample size minus 1 | \[ \frac{\Sigma f(x_{m} - \bar{x})^2}{n-1} \] |
| 9. Take the square root of the value from step 8 | \[ \sqrt{ \frac{\Sigma f(x_{m} - \bar{x})^2}{n-1} } \] |
The process to find the grouped SD is similar to that of a simple standard deviation. Following these steps, we’re able to find the grouped standard deviation from the earlier example.
| Test Score Categories | Frequency 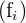 | 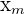 |  | 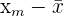 |  | 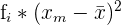 |
| 10 - 20 | 1 | (20-10)/2 = 15 | 15*1 = 15 | 15-64.7 = -49.7 | (-49.7)^2 = 2474.2 | 1*2474.2 = 2474.2 |
| 20 - 30 | 8 | 25 | 200 | -39.7 | 1579.4 | 12635.0 |
| 30 - 40 | 5 | 35 | 175 | -29.7 | 884.5 | 4422.7 |
| 40 - 50 | 9 | 45 | 405 | -19.7 | 389.7 | 3507.5 |
| 50 - 60 | 8 | 55 | 440 | -9.7 | 94.9 | 759.2 |
| 60 - 70 | 10 | 65 | 650 | 0.3 | 0.1 | 0.7 |
| 70 - 80 | 75 | 75 | 5625 | 10.3 | 105.2 | 7892.9 |
| Total | 116 | 7510 | 31692.2 |
\[
\bar{x} = \dfrac{7510}{116} = 64.7
\]
\[
s_{grouped} = \sqrt{\dfrac{3169.2}{116-1}} = \sqrt{275.6} = 16.6
\]
Characteristics of Standard Deviation
The standard deviation will, naturally, be different for all data sets. However, there are a couple of characteristics of the SD that will always hold true.
- The standard deviation is always either positive or zero. This is because all values that we sum are squared values.
- The standard deviation is zero if all values in the data set are equal to the mean.
- The standard deviation is sensitive to outliers or extreme values.
Interpreting the Standard Deviation
Recall the rules of thumb from earlier, where the higher the standard deviation, the higher the variability. While the words “higher” variability might imply that it is something we don’t desire, a higher variability in the data set isn’t always a “bad” thing.
Interpreting the standard deviation can be difficult because of the fact that it depends on the context of the question someone is trying to solve. It’s helpful to stay away from thinking of a high or low standard deviation as having a “bad” or “good” standard deviation.
Instead, remember the definition and calculation of the SD, which is a measure of how widely spread the data is around the mean. Let’s say, for example, two restaurants want to measure which dish is each customer's favourite through a 100 point scale where 0 is the lowest and 100 is the highest.
| Restaurant A | Restaurant B | |
| Pasta | 20 | 60 |
| Salad | 10 | 90 |
| Rice | 30 | 70 |
| Burger | 25 | 80 |
| Mean | 21.3 | 75 |
| SD | 7.4 | 11.2 |
Restaurant A has a lower standard deviation than restaurant B, which means that people rated each dish in a manner that was more consistent to the mean. However, people rated Restaurant A’s dishes quite low, with an average of 21 points. While Restaurant B’s ratings have a higher SD, their mean rating is a lot higher than Restaurant A.
It is important to always take the standard deviation in the context of things like the average, the question you want to ask, or the people in your sample.
Problem 1: Grouped Standard Deviation
You’re studying the amount of time students spend using social media. You find a study that was performed in a classroom of students that displays data on how many hours per week each student spent on one or more social media platforms. Given the data below, find and interpret the grouped standard deviation, rounding to the nearest tenth.
| Number of Hours | Number of Students | 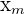 |  | 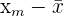 |  | 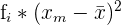 |
| 0 - 2 | 5 | |||||
| 2-4 | 13 | |||||
| 4-6 | 24 | |||||
| 6-8 | 17 | |||||
| 8-10 | 6 |
Solution to Problem 1
In this problem you were asked to
- Calculate the group standard deviation
- Interpret the standard deviation
While we’re not directly given the frequency, we know that the number of students in each category is the frequency. From previous examples, we also know that the total number of students is our sample size. Using this information, we calculate the following.
| Number of Hours | Number of Students (f) | 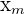 |  | 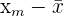 |  | 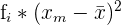 |
| 0 - 2 | 5 | 1 | 5 | -4.2 | 17.5 | 87.6 |
| 2-4 | 13 | 3 | 39 | -2.2 | 4.8 | 62.0 |
| 4-6 | 24 | 5 | 120 | -0.2 | 0.0 | 0.8 |
| 6-8 | 17 | 7 | 119 | 1.8 | 3.3 | 56.0 |
| 8-10 | 6
| 9 | 54 | 3.8 | 14.6 | 87.3 |
Where we calculate the following:
\[ n=65 \]
\[ \Sigma x_{m}*f_{i} = 337 \]
\[ \bar{x}=\dfrac{337}{65}=5.2 \]
\[ \Sigma f_{i}*(x_{m}-\bar{x})^2 = 293.8 \]
\[ \dfrac{\Sigma f_{i}*(x_{m}-\bar{x})^2}{n-1} = \dfrac{293.8}{65-1} = 4.6 \]
\[ \sqrt{4.6} = 2.1 \]













Can you help me answer my activities