Chapters
- Exercise 1
- Exercise 2
- Exercise 3
- Exercise 4
- Exercise 5
- Exercise 6
- Exercise 7
- Exercise 8
- Exercise 9
- Exercise 10
- Solution of exercise 1
- Solution of exercise 2
- Solution of exercise 3
- Solution of exercise 4
- Solution of exercise 5
- Solution of exercise 6
- Solution of exercise 7
- Solution of exercise 8
- Solution of exercise 9
- Solution of exercise 10

Exercise 1
Find the total possible amount of eight-digit palindromics. Also, how many nine-digit palindromics are there? (Palindromic: a number whose digits read the same backwards and forwards.)
Exercise 2
Four different math, six different physics and two different chemistry textbooks are placed on a shelf. What is the number of possible combinations of arranging the textbooks if:
- The textbooks from each subject must be grouped together.
- Only the math textbooks need to be grouped together.
Exercise 3
A boy has five coins, each of a different value. How many different sums of money can be totaled with these five coins?
Exercise 4
5 red, 2 white and 3 blue balls are arranged in a row. If the balls of like color are not distinguished from each other, how many possible ways can they be ordered?
Exercise 5
With the dot and dash system of Morse code, how many different signals can be sent using four clicks or less?
Exercise 6
Eight people are seated at a dinner table at a political function. How many ways can they sit if the president and secretary always have to be seated next to one another?
Exercise 7
How many diagonals does a pentagon have and how many triangles can be formed with its vertices?
Exercise 8
Suppose there is a set of 8 candies. In how many ways, 4 candies can be selected from this set (without repetition)?
Exercise 9
Suppose there is a set of 10 vegetables. In how many ways, 6 vegetables can be selected from this set (without repetition)?
Exercise 10
Suppose Alice has 5 red balls and 4 green balls. She wants to arrange all the balls in a row in such a way that the red balls occupy the odd positions. How many arrangements are possible?
Solution of exercise 1
Find the total possible amount of eight-digit palindromic. Also, how many nine-digit palindromic are there? (Palindromic: a number whose digits read the same backwards and forwards.)




Solution of exercise 2
Four different math, six different physics and two different chemistry textbooks are placed on a shelf. What is the number of possible combinations of arranging the textbooks if:
The textbooks from each subject must be grouped together.


Only the math textbooks need to be grouped together.


Solution of exercise 3
A boy has five coins, each of a different value. How many different sums of money can be totaled with these five coins?

Solution of exercise 4
5 red, 2 white and 3 blue balls are arranged in a row. If the balls of like color are not distinguished from each other, how many possible ways can they be ordered?

Solution of exercise 5
With the dot and dash system of Morse code, how many different signals can be sent using four clicks or less?
The order of the elements does matter.
The elements can be repeated.

Solution of exercise 6
Eight people are seated at a dinner table at a political function. How many ways can they sit if the president and secretary always have to be seated next to one another?
There are two groups that the elements can be divided into for solving this problem. The first has two people (president and secretary) and the second has 7 people.
The order of the elements does matter.
The elements cannot be repeated.

Solution of exercise 7
How many diagonals does a pentagon have and how many triangles can be formed with its vertices?
First, the lines that can be drawn between 2 vertices need to be determined.
The order of the elements does not matter.
The elements cannot be repeated.
The sides that determine 5 straight lines that are not diagonal need to be subtracted.
 diagonals
diagonals
 triangles
triangles
Solution of exercise 8
In this example, we are given the following information:
The total number of candies = 8
Number of candies we want to select = 4
Is repetition allowed = No
The formula for calculating the permutations when no repetition is allowed is given below:
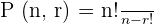
Substitute the values in the above formula to get the number of ways the candies can be selected:


Hence, we can select 4 candies from a set of 8 candies in 1680 ways.
Solution of exercise 9
In this example, we are given the following information:
The total number of vegetables = 10
Number of vegetables we want to select = 6
Is repetition allowed = No
The formula for calculating the permutations when no repetition is allowed is given below:
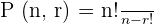
Substitute the values in the above formula to get the number of ways the candies can be selected:


Hence, we can select 6 vegetables from a set of 10 vegetables in 151200 ways.
Solution of exercise 10
We are given the following information in this problem:
The number of balls = 9
The odd positions for red balls will be 1, 3, 5, 7, 9
The red balls can occupy 5 odd positions:


There are 4 positions left which will be occupied by the the green balls:


Hence, the total number of arrangements possible are:














I need to learn
I must say everything is superb I wish I could access to most of my maths topics here! Questions are easy to comprehend. Thanks for your help.
in how many ways can be 5 red balls and green balls be arranged in a row of no two green balls can be next to each other?
Great job but explanations are too complex