Chapters
You might have heard the word "Binomial" before, maybe, in the Algebra. In the world of Algebra, we use binomial to find the equation of an expression that has the power/exponent more than 2 and that expression has only "2" term. However, in the world of statistics, the binomial works the same but the purpose here is different. In Binomial Distribution, we use binomial to calculate the probability of "SUCCESS" and "FAILURE" only of events that are repeated more than twice. For example, a coin is tossed and we all know that either the outcome will be head or tail. The coin is tossed 50 times, now we need to find what will be the probability of getting head in that 50 tosses and to find the probability of tail, we will subtract the probability of heads from 1 (since the sum of all probability is equal to 1).
There are some conditions for using the binomial distribution. An experiment is modeled on the binomial distribution if:
- In each trial of the experiment, there should be only two possible outcomes: the success of that event (denoted by p) and the failure of the event (denoted by q).
- The probabilities of the event should remain constant throughout the event.
- We usually focus on finding the probability of success (which is p). To find the failure of the event (which is q), we subtract the probability of success from 1.
- Lastly, the outcome obtained in each trial is independent of the previous outcomes.
All right! So, let's construct a proper definition of Binomial distribution. A Binomial Distribution is the calculation of the possible number of successful outcomes in a given number of trials. Each trial has the same probability of success throughout the event and the outcome obtained in each trial is independent of the previous outcomes.

Random Binomial Variable
The binomial variable is a discreet random variable that can only take the values 0, 1, 2, 3, 4, ..., n assuming that n trials have been conducted.
Example
k = 6, when flipping a coin 10 times and 6 heads are obtained.
Binomial Distribution
Whenever we express a binomial distribution, we express it as B(n,p). Below is the formula of binomial distribution:

Where n is the number of trails,
k is the number of successive trials,
p is the probability of success,
and q is the probability of failure.
To find the value of q, you need to subtract the value of p from 1.
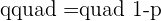
To find the binomial coefficient, you need to use the binomial formula which is:
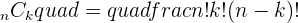
Application of Binomial Distribution
The binomial distribution is mostly used in testing or making predictions. For example, researchers made a new drug that can cure cancer, it can either cure cancer (which is the success probability) or it won't (which is the failure probability). Another example is of a lottery, you bought a ticket from 2000 tickets. Now there might be people who bought tens, hundreds of tickets. With the help of binomial distribution, you can find the probability of your or anyone's success.
Example
Q. The latest novel by an author has been very successful to the point that 80% of avid readers have already read it.
(a) What is the probability that within a group of four avid readers, exactly two of them have already read the novel?
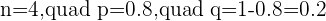
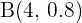

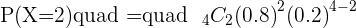
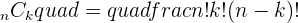






(b) What about a maximum of two people?
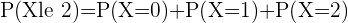
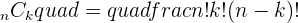
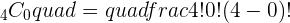 *0! is equal to 1
*0! is equal to 1


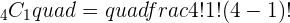
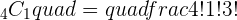
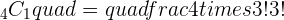


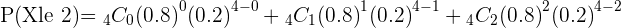
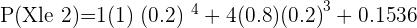
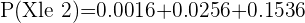

Q. A light bulb manufactures 100 light bulbs. Out of 100 light bulbs, 8 light bulbs have high chances of malfunction. A bulb is chosen at random, find the probability of the chosen light bulb is broken.

*This question is tricky. You need to understand its nature first. It is common sense that broken bulbs should be the failure which means that 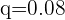 but the question asked to find the probability of the broken bulb. The binomial distribution provides the probability of success only, that is why you should take the probability of broken bulb as the probability of success.*
but the question asked to find the probability of the broken bulb. The binomial distribution provides the probability of success only, that is why you should take the probability of broken bulb as the probability of success.*
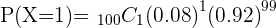
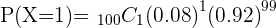

*We could have found the probability of the broken bulb by finding the probability of working bulb and then subtract it from 1. This is another method to find the probability of the broken bulb but there is a problem. If you try to find the value of 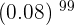 , it will show you zero because the value is so low that many calculators will show you zero.
, it will show you zero because the value is so low that many calculators will show you zero.
Standard Deviation
To calculate the standard deviation of a binomial distribution, below is the formula:

Where n is the number of trails,
and p is the probability of success.
Variance
To calculate the variance of a binomial distribution, below is the formula:
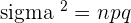
Where n is the number of trails,
p is the probability of success.
and q is the probability of failure.
Example
Q. The probability of a defective item produced by a factory is  . If a shipment of 10,000 items are sent to a store, determine the expected number of defective items, the variance and standard deviation for the shipment.
. If a shipment of 10,000 items are sent to a store, determine the expected number of defective items, the variance and standard deviation for the shipment.



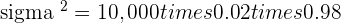
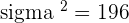
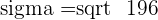
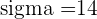













In question 3 : i think you have missed 9 . it should be (10*9)/2 (1/5)^2(4/5)^8
good job
Can you give me 5 real-life problems involving random variables?
i need it now please
A) 0.2668
B) 0.33965
C) 0,04575
D) 0.97175
Hello please
Can you please help me with question 6?
Thank you
CORRECTION
p (AUB) = 0.05 + ( (1 – 0.05 ) x 0.1) = 0.145
in 6th question a part
Pls explain question six 2
For ex.2 part.3 there’s a rounding error – the answer is 0.165
Please help me work these cumulative binomial probability.
In a particular strain of staphylococcus product abdominal cramps in 30% of person infected. At a clinic 10 persons ate contaminated food and were infected with the organisms, find:
A) exactly three people will develop the symptoms.
B) between 3 and 7 inclusively will develop the symptoms.
C) more than 5 people will develop the symptoms.
D) at least one person will develop the symptoms.
A) 0.2668
B) 0.33965
C) 0,04575
D) 0.97175