Axiomas de la probabilidad

1.La probabilidad es positiva y menor o igual que 1.

0 ≤ p(A) ≤ 1

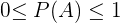
2. La probabilidad del suceso seguro es 1.

p(E) = 1

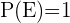
3.Si A y B son incompatibles, es decir A B = entonces:

p(A B) = p(A) + p(B)

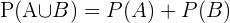
Propiedades de la probabilidad

1 La suma de las probabilidades de un suceso y su contrario vale 1, por tanto la probabilidad del suceso contrario es:

2 Probabilidad del suceso imposible es cero.

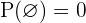
3 La probabilidad de la unión de dos sucesos es la suma de sus probabilidades restándole la probabilidad de su intersección.

4 Si un suceso está incluido en otro, su probabilidad es menor o igual a la de éste.

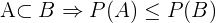
5 Si A₁, A₂, ..., A_k son incompatibles dos a dos entonces:

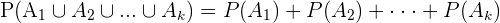
6 Si el espacio muestral E es finito y un suceso es S = {x₁, x₂, ..., x_n} entonces:

Por ejemplo la probabilidad de sacar par, al tirar un dado, es:

P(par) = P(1) + P(2) + P(3)