Temas

El espacio muestral (o espacio de sucesos)
Es probabilidad, el espacio muestral, denotado por 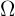 (o en ocasiones como
(o en ocasiones como  ), es el conjunto de todos los posibles resultados al realizar un experimento aleatorio.
), es el conjunto de todos los posibles resultados al realizar un experimento aleatorio.
Ejemplos
1 Lanzar un dado
Consideremos el experimento de lanzar un dado. Sabemos que el dado tiene 6 caras con cada una con un distinto número entero que van del  al
al 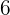
 , por lo tanto, nuestro espacio muestral con todos los posibles resultados que podemos tener al lanzar un dado sería
, por lo tanto, nuestro espacio muestral con todos los posibles resultados que podemos tener al lanzar un dado sería
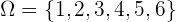
2 Lanzar dos monedas
Consideremos el experimento de lanzar dos monedas. Una moneda tiene dos lados solamente, cara ( ) o cruz (
) o cruz (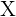 ). Como nosotros estamos considerando lanzar dos monedas, nuestros resultados serían pares, por lo tanto, nuestro espacio muestral con todos los posibles resultados que podríamos obtener sería
). Como nosotros estamos considerando lanzar dos monedas, nuestros resultados serían pares, por lo tanto, nuestro espacio muestral con todos los posibles resultados que podríamos obtener sería
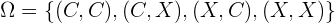
Otro concepto importante es el de evento (o suceso), denotado por 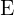 . Un evento es un subconjunto del espacio muestral, o de forma menos formal, el hecho de que ocurran "ciertos casos".
. Un evento es un subconjunto del espacio muestral, o de forma menos formal, el hecho de que ocurran "ciertos casos".
Ejemplo:
Considerar el hecho de que al lanzar el dado caiga un 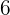 o un
o un 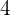 estaría dado por el subconjunto
estaría dado por el subconjunto
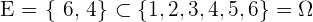
Un evento elemental (o suceso elemental) es un evento constituido por un único elemento,  .En otras palabras, es un evento que solo considera un resultado (también se conocen los eventos elementales como resultados por sí mismos).
.En otras palabras, es un evento que solo considera un resultado (también se conocen los eventos elementales como resultados por sí mismos).
Ejemplo:
Considerar el hecho de lanzar solo una vez dos monedas al mismo tiempo y que ambas caigan cruz 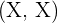 es un evento elemental ya que estaría dado por el subconjunto
es un evento elemental ya que estaría dado por el subconjunto

Recordemos que cada par, 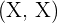 , por ejemplo, es un único resultado a pesar de que está compuesto por dos elementos individuales (esto ya que consideramos el hecho de lanzar dos monedas distintas).
, por ejemplo, es un único resultado a pesar de que está compuesto por dos elementos individuales (esto ya que consideramos el hecho de lanzar dos monedas distintas).
Resultados igualmente probables (equiprobables)
En algunos casos la probabilidad considera los distintos resultados de un experimentos igualmente probables. En estos casos, en un espacio muestral con 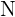 posibles resultados con la misma probabilidad de ocurrir, a cada resultado se le asigna la probabilidad de
posibles resultados con la misma probabilidad de ocurrir, a cada resultado se le asigna la probabilidad de  .
.
En un espacio muestra con resultados igualmente probables, la probabilidad de que ocurra un evento se vuelve fácil de calcular:

Unión de eventos
Dados dos eventos,  y
y  , definimos la unión de eventos, denotada por
, definimos la unión de eventos, denotada por  , como el evento formado por todos los elementos que están en
, como el evento formado por todos los elementos que están en  o en
o en  . Es decir, el evento
. Es decir, el evento  se verifica cuando ocurre uno de los dos,
se verifica cuando ocurre uno de los dos,  o en
o en  , o ambos.
, o ambos.
 se lee como "
se lee como " unión
unión  ".
".
Observación. Notemos que en realidad la unión de dos eventos no es nada más que la unión de sus conjuntos.
Ejemplo:
Consideramos el experimento que consiste en lanzar un dado, consideremos el evento de caiga un número par como  y el evento de que caiga un número que sea múltiplo de tres como
y el evento de que caiga un número que sea múltiplo de tres como  . Calculemos la unión los eventos
. Calculemos la unión los eventos  y
y  (
( ):
):




Propiedades de la unión de eventos
-
- Conmutatividad
Dados dos eventos
 y
y  se cumple que
se cumple que .
.
- Conmutatividad
-
- Asociativadad
Dados los eventos
 ,
,  y
y  se cumple que
se cumple que .
.
- Asociativadad
-
- Idempotencia
Para todo evento
 se cumple que
se cumple que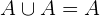 .
.
- Idempotencia
-
- Distributividad
Dados los eventos
 ,
,  y
y  se cumple que
se cumple que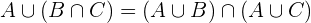
y

- Distributividad
-
- Simplificación
Dados dos eventos
 y
y  se cumple que
se cumple que .
.
- Simplificación
-
- Elemento neutro
Para todo evento
 se cumple que
se cumple que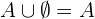 .
.En donde
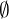 se conoce como el evento vacío.
se conoce como el evento vacío. - Absorción
Sea
 un evento cualquiera y
un evento cualquiera y 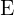 cualquier otro evento más grande que contenga al evento
cualquier otro evento más grande que contenga al evento  (puede ser incluso el mismo espacio muestral
(puede ser incluso el mismo espacio muestral 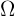 ), entonces se cumple que
), entonces se cumple que .
.
- Elemento neutro
Probabilidad de la unión de eventos
Consideremos dos eventos  y
y  con probabilidades
con probabilidades  y
y  , respectivamente. Entonces, tenemos que la probabilidad de su unión,
, respectivamente. Entonces, tenemos que la probabilidad de su unión,  , está dada por
, está dada por
 .
.
Esto nos da dos casos importantes a considerar. Cuando  y cuando
y cuando  .
.
Probabilidad de la unión de sucesos compatibles
Decimos que dos eventos  y
y  son compatibles cuando contienen al menos un evento elemental en común. En otras palabras, si ambos consideran al menos un mismo resultado.
son compatibles cuando contienen al menos un evento elemental en común. En otras palabras, si ambos consideran al menos un mismo resultado.
Cuando dos eventos  y
y  son compatibles, su intersección no es vacía (es distinta del conjunto vacío,
son compatibles, su intersección no es vacía (es distinta del conjunto vacío,  ). Esto es
). Esto es
 .
.
En este caso, como la intersección no es vacía, y sus elementos (resultado que considera) pertenecen al espacio muestral, se tiene que  . Así, consideramos la ecuación (\ref{ProbabilidadUnion}) para calcular la probabilidad de
. Así, consideramos la ecuación (\ref{ProbabilidadUnion}) para calcular la probabilidad de  .
.
 .
.
Ejemplo
Consideremos el experimento de lanzar un dado y los siguientes eventos:
-
- Que al lanzar el dado el número sea un múltiplo de tres,

- Que al lanzar el dado el número sea un múltiplo de tres,
- Que al lanzar el dado caiga en el número
 ,
,  .
.
Notemos que  , por lo tanto, son conjuntos compatibles. Además, tenemos que
, por lo tanto, son conjuntos compatibles. Además, tenemos que  y
y  . Aplicando la fórmula de la ecuación (\ref{ProbabilidadUnion}), tenemos que
. Aplicando la fórmula de la ecuación (\ref{ProbabilidadUnion}), tenemos que

Probabilidad de la unión de eventos incompatibles
Decimos que dos eventos  y
y  son incompatibles cuando no tienen ningún elemento en común. En otras palabras, si un resultado que es considerado en
son incompatibles cuando no tienen ningún elemento en común. En otras palabras, si un resultado que es considerado en  no está en
no está en  y viceversa.
y viceversa.
Otra forma es que dos eventos  y
y  son incompatibles cuando su intersección es vacía (es el conjunto vacío,
son incompatibles cuando su intersección es vacía (es el conjunto vacío,  ). Esto es
). Esto es
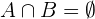
Tenemos que la probabilidad del conjunto vacío es  ya que este evento no considera ningún resultado. Notemos que, debido a esto, tendríamos que la ecuación (\ref{ProbabilidadUnion}) se reduce a
ya que este evento no considera ningún resultado. Notemos que, debido a esto, tendríamos que la ecuación (\ref{ProbabilidadUnion}) se reduce a
 .
.
Ejemplo
Consideremos el experimento de lanzar un dado y los siguientes eventos:
-
- Que al lanzar el dado el número sea primo menor a 4,

- Que al lanzar el dado el número sea primo menor a 4,
- Que al lanzar el dado caiga en el número
 o el número
o el número  ,
,  .
.
Notemos que  , por lo tanto, son conjuntos incompatibles. Además, tenemos que
, por lo tanto, son conjuntos incompatibles. Además, tenemos que  y
y  . Aplicando la fórmula de la ecuación (\ref{ProbabilidadIncompatibles}), tenemos que
. Aplicando la fórmula de la ecuación (\ref{ProbabilidadIncompatibles}), tenemos que














Apuntes es una plataforma dirigida al estudio y la práctica de las matemáticas a través de la teoría y ejercicios interactivos que ponemos a vuestra disposición. Esta información está disponible para todo aquel/aquella que quiera profundizar en el aprendizaje de esta ciencia. Será un placer ayudaros en caso de que tengáis dudas frente algún problema, sin embargo, no realizamos un ejercicio que nos presentéis de 0 sin que hayáis si quiera intentado resolverlo. Ánimo, todo esfuerzo tiene su recompensa.
de cuantas foras distintas se pueden sentarse 8 personas alrededr de una mesa redonda?pasos para reslverlo por favor
Tengo 12 personas y se requiere formar equipos de cuatro personas, si dos personas no pueden estar juntas, cuantos posibilidades tengo para armar equipos?
En una universidad el 60% de los estudiantes aprueban contabilidad 70% aprueba inglés y el 30% aprueba ambos cursos si un alumno es seleccionado a la zar encuentra la sig probabilidad condicional
A)para contabilidad dado que pasó inglés
Halla el coeficiente de a⁵ b⁷ en la expansión de (a+b)¹²
El ejercicio nº 3 es incorrecto. El evento E tiene una probabilidad del 5% es decir 0,05 no del 0,005 (5 por mil).
Por favor indicame el artículo pues me sale el de Ejercicios del binomio de Newton.
De 120 formas