Concepto de combinaciones con repetición
Las combinaciones con repetición de m elementos tomados de 
en 
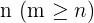, son los distintos grupos formados por n elementos de manera que:
No entran todos los elementos.
No importa el orden.
Sí se repiten los elementos.
Al número de combinaciones con repetición se de denotará por 
. El problema, entonces, consiste en determinar el valor de 
, el cual podemos calcular con la siguiente fórmula:
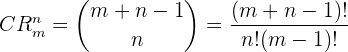
El número se representa también por el símbolo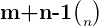 
. Cuando se utiliza esta notación, este número se llama coeficiente binomial.
Ejemplo de combinaciones con repetición
1 En una bodega hay cinco tipos diferentes de botellas. ¿De cuántas formas se pueden elegir cuatro botellas?
Solución:
No entran todos los elementos. Sólo elije 
.
No importa el orden. Da igual que elija 
botellas de anís y de ron, que de ron y de anís.
Sí se repiten los elementos. Puede elegir más de una botella del mismo tipo.
¿Te ha gustado este artículo? ¡Califícalo!
Cargando...
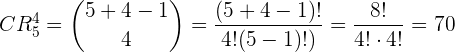
Apuntes es una plataforma dirigida al estudio y la práctica de las matemáticas a través de la teoría y ejercicios interactivos que ponemos a vuestra disposición. Esta información está disponible para todo aquel/aquella que quiera profundizar en el aprendizaje de esta ciencia. Será un placer ayudaros en caso de que tengáis dudas frente algún problema, sin embargo, no realizamos un ejercicio que nos presentéis de 0 sin que hayáis si quiera intentado resolverlo. Ánimo, todo esfuerzo tiene su recompensa.
Utiliza un diagrama de árboles para calcular cuántas formas hay para repartir cuatro dulces de diferentes sabores entre cuatro personas sin ninguna puede quedar sin dulce
Probabilidad de que al lanzar un dado 5 veces salga 3,2,1,5,6,3
De cuántas formas diferentes puedo sentar a 7 personas en dos mesas de 3 y 4 sillas respectivamente?
Muy bueno, solo que, el total d elemento u objetos es la letra ‘n’ y la cantidad de elementos tomados e ‘r’, C(n,r) . El ejmplo excelente. Saludos desde Oruro – Bolivia
Entiendo tu sugerencia pero se usa como total de elementos m yla cantidad de elementos tomados n de n, entonces son letras diferentes pero la idea es la misma, lo que tu sugieres viene en algunos libros, pero lo importante es entender.
En el problema 8, deberíamos esclarecer que la comisión la ocupan 3 alumnos que tienen diferentes cargos en la misma. Sin eso, alguna persona podría pensar que se trata de una combinación y no de una permutación. ya que el orden no importaría si todos tuvieran un mismo rol.
Por lo general cuando se habla de una comisión se piensa que todos ya saben que hay 3 diferentes cargos, pero entiendo lo que sugieres ya que sería más correcto, pero hasta los libros no lo aplican.
de cuantas foras distintas se pueden sentarse 8 personas alrededr de una mesa redonda?pasos para reslverlo por favor