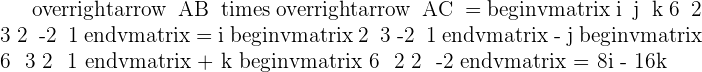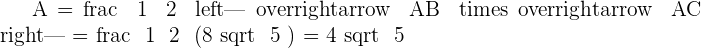Chapters

Exercise 1
Find two unit vectors for  and
and 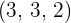 and determine the orthogonal vector for the two.
and determine the orthogonal vector for the two.
Exercise 2
Find a unit vector that is perpendicular to  and
and  .
.
Exercise 3
Given the vectors 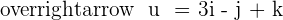 and
and 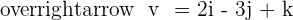 , find the product
, find the product  and verify that this vector is orthogonal to
and verify that this vector is orthogonal to  and
and 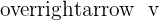 . Also, find the vector
. Also, find the vector 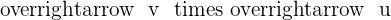 and compare it with
and compare it with  .
.
Exercise 4
Consider the following figure:
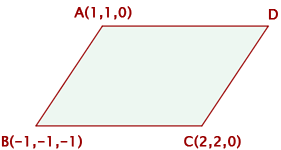
Determine:
1 The coordinates of D if ABCD is a parallelogram.
2 The area of the parallelogram.
Exercise 5
Given the points 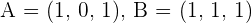 and
and 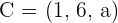 , determine:
, determine:
1 What values of a are collinear.
2 Determine if values exist for a so that A, B, and C are three vertices of a parallelogram of area  . If values do exist, determine the coordinates of C:
. If values do exist, determine the coordinates of C:
Exercise 6
 and
and 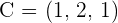 are the three vertices of a triangle.
are the three vertices of a triangle.
1. Calculate the cosine of each of the three angles in the triangle.
2. Calculate the area of the triangle.
Solution of exercise 1
Find two unit vectors for  and
and 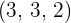 and determine the orthogonal vector for the two.
and determine the orthogonal vector for the two.



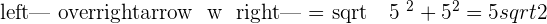

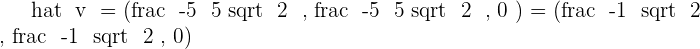
Solution of exercise 2
Find a unit vector that is perpendicular to  and
and  .
.

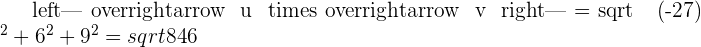

Solution of exercise 3
Given the vectors 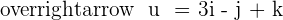 and
and 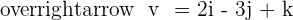 , find the product
, find the product  and verify that this vector is orthogonal to
and verify that this vector is orthogonal to  and
and 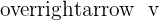 . Also, find the vector
. Also, find the vector 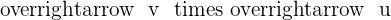 and compare it with
and compare it with  .
.

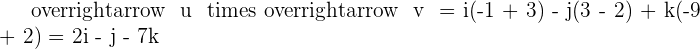
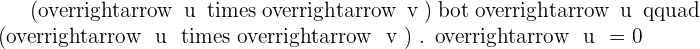
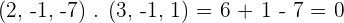
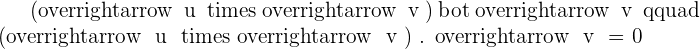

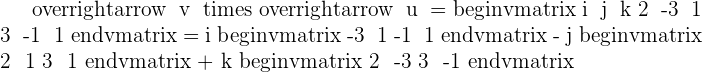
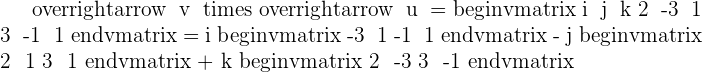
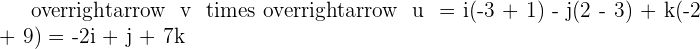
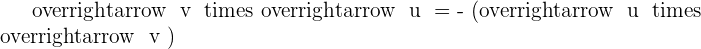
Solution of exercise 4
Consider the following figure:

Determine:
1 The coordinates of D if ABCD is a parallelogram.
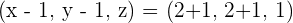
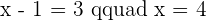
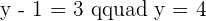
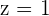
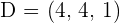
2 The area of the parallelogram.

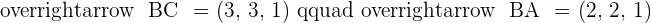

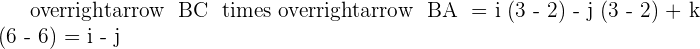

Solution of exercise 5
Given the points 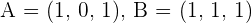 and
and 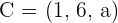 , determine:
, determine:
1 What values of a are collinear.
If A, B, and C are collinear, the vectors  and
and 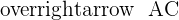 are linearly dependent and have proportional components.
are linearly dependent and have proportional components.
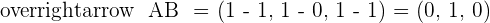
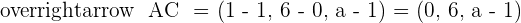

2 Determine if values exist for a so that A, B, and C are three vertices of a parallelogram of area  . If values do exist, determine the coordinates of C:
. If values do exist, determine the coordinates of C:
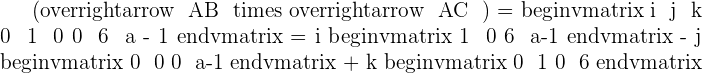
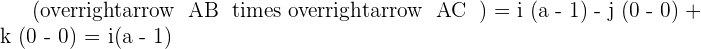
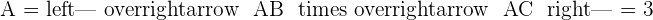
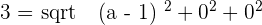
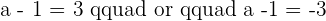
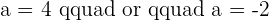
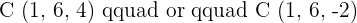
Find various Maths tutors near me on Superprof.
Solution of exercise 6
 and
and 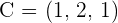 are the three vertices of a triangle.
are the three vertices of a triangle.
1. Calculate the cosine of each of the three angles in the triangle.

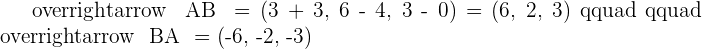
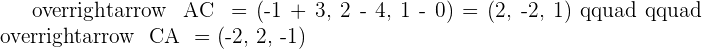

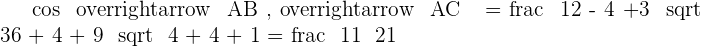
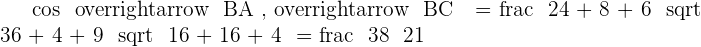

2. Calculate the area of the triangle.