In this article, we will discuss what is the basis vector.
Suppose V is a subspace of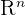 
for some value of n. A collection A of vectors V which is equal to 
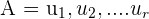is termed as a basis of V if it fulfills the following two criteria:
- The set of vectors A is linearly independent
- The set of vectors A spans V
If one of the above two criteria is not fulfilled, then the collection of vectors A is not a basis for V. If the set of vectors A spans V, then it has sufficient vectors so that each vector in V can be expressed as a linear combination of the vectors in the set. If the set of the vectors is linearly independent, then it means that this set does not have enough vectors so that few vectors can be expressed as a linear combination of others. Thus, we can say that the basis vector is of the right size, i.e., it is large enough to span the vector space, but it is not large enough to be dependent.
For instance, the set {n, k} is a basis for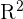 
because it spans 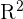. The vectors n and k in the set are linearly independent because neither of these vectors is multiples of each other. This is referred to as the standard basis for 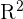. Similarly, the set {n , k, r} is known as the standard basis for 
.
We can define the basis of vectors as:
"Three linearly dependent vectors
,
, and
form a basis because any vector in the vector space can be set as a linear combination of these vectors"
Mathematically, it is expressed as:
The coordinates of the vectors that form the base are 
Orthogonal Basis
The three basis vectors are mutually perpendicular.
Orthonormal Basis
The three basis vectors are mutually perpendicular and also have a length of one.
For instance, consider the vectors 
.
Here, 
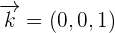
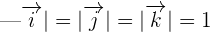
The base formed by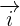 
, 
, and 
is known as the standard basis or canonical basis.
No, we will solve some examples in which we will demonstrate that the given set of vectors form the basis or not.
Example 1
Determine whether the vectors 
, 
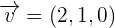, and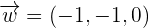 
form a basis or not and calculate the coordinates of the vector (1, -1, 0) on that basis.
Solution
In the first step of solving the problem, we will multiply the vectors with a, b and c respectively.
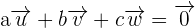
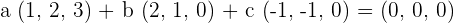
We can write the above equation as system of equations like this:
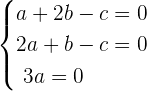
Now, we will use the above equation and convert it into the matrix form like this:
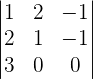
We will calculate the determinant of the above matrix using the formula of calculating the determinant of the 3x3 matrix.
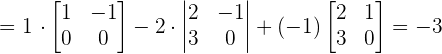
Since the determinant is not equal to zero, hence the three vectors are linearly independent and form the basis.
Example 2
Determine whether the vectors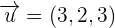 
, 
, and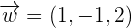 
form a basis or not.
Solution
In the first step of solving the problem, we will multiply the vectors with a, b and c respectively.
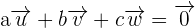
We can write the above equation as system of equations like this:
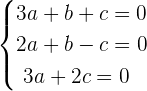
Now, we will use the above equation and convert it into the matrix form like this:
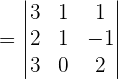
We will calculate the determinant of the above matrix using the formula of calculating the determinant of the 3x3 matrix.
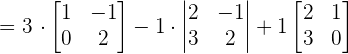
Since the determinant of the matrix is not equal to zero, hence the three vectors are linearly independent and form the basis.
Example 3
Determine whether the vectors 
, 
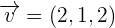, and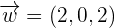 
form a basis or not.
Solution
In the first step of solving the problem, we will multiply the vectors with a, b and c respectively.
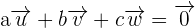
We can write the above equation as system of equations like this:
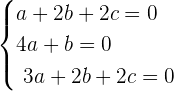
Now, we will use the above equation and convert it into the matrix form like this:
We will calculate the determinant of the above matrix using the formula of calculating the determinant of the 3x3 matrix.
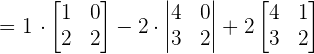
Since the determinant of the matrix is not equal to zero, hence the three vectors are linearly independent and form the basis.
Find various Maths tutor near me on Superprof.
Example 4
Determine whether the vectors 
, 
, and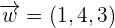 
form a basis or not.
Solution
In the first step of solving the problem, we will multiply the vectors with a, b and c respectively.
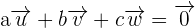
We can write the above equation as system of equations like this:
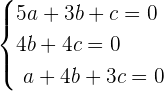
Now, we will use the above equation and convert it into the matrix form like this:
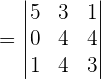
We will calculate the determinant of the above matrix using the formula of calculating the determinant of the 3x3 matrix.
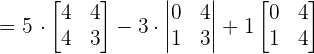
Since the determinant of the matrix is not equal to zero, hence the three vectors are linearly independent and form the basis.
Example 5
, 
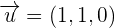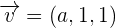and 
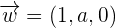form the basisSolution
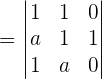
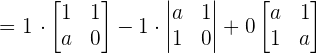
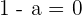
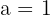
To be linearly independent the determinant of the matrix should not be zero Hence, we can say that if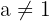 
, then the vectors form the basis.
Did you like this article? Rate it!
Loading...
