Chapters
Whether you are an engineer or an astrologist, you still need to understand how vectors are projected to determine the magnitude as well as the direction of force been applied to any object. This valuable information can help us to find different sets of data such as speed, heat, strength, direction, and many other things. Projecting vector into another is one of the fundamentals of physics and maths. Without the projection of vectors, you can't identify the nature of force and this can lead to many errors. To avoid these errors, scientists found a way to find the true nature of the force and how they did this? By projecting vectors. In this lesson, you will learn about two different vector projections.
Scalar Projection
Scalar projection is basically the magnitude of the vector projection. To understand scalar projection, you need to know about the dot product. The dot product of any two vectors results in a scalar quantity that describes the length (magnitude) of the particular vector. The question is what is scalar projection then? It is the projection when you dot product the unit vector with the vector in a particular direction.
If the scalar projection results in a positive value that indicates the angle between both vectors is less than 90∘. It also means that both vectors are in the same direction. On the other hand, if the scalar projection results in a negative value, that indicates the angle between both vectors is greater than 90∘. This also tells us that the vectors are in opposite directions.
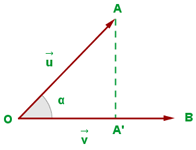
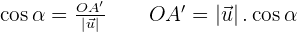
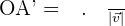
Vector Projection
One of the most frequently asked questions is why do we project one vector to another? To find how much a vector is equal to another vector in the same direction. The vector projection is the unit vector of 
by the scalar projection of u on v. In mathematical language, this is written as 
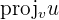. It means that the vector "v" is projected onto "u". In simple words, a new vector is projected and in the direction of u. Vector projection is frequently used in physics and maths. The reason is that it is used to solve different forces acting on different bodies with respect to its component vectors. At this point, you might be confused so let's make this simple. A vector in any direction has two components, one is parallel to the 2nd vector and one is perpendicular to the 2nd vector. In Physics, we don't use the 2nd vector as the frame of reference, we use the axis as the frame of reference. The axes are abscissa and ordinate. The x-axis is called the 
component while the y-axis is called the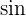 
component. In easy words, the concept of vector projection is the same but the frame of reference is different.
For example, you are trying to lift a box at a certain angle. The direction in which you are lifting the box can be solved in two ways. In easy words, the total force that you are applying to the box has two parts. One is the pulling force and one is the lifting force. This can be solved by a vector projection. A part of the total force is wasted in lifting the box from one point to another and the remaining part of the force is wasted by pulling the box from one point to another. The total force will be the sum of lifting and pulling force and it will be written like this:
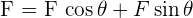
The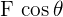 
and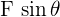 
are the vector projections on the total force vector. The vector projection is the unit vector of by the scalar projection of u on v.
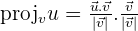
The scalar projection of u on v is the magnitude of the vector projection of u on v.
Examples
Calculate the vector projection of 
on the vector 
.
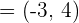Calculate the vector projection of 
on the vector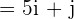 
.
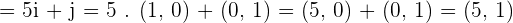
Calculate the scalar projection of the vector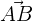 
on the vector 
if: 
and 
.
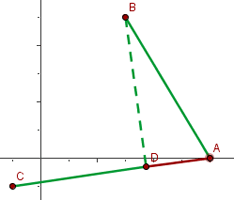
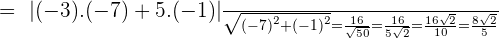
If the vertices of a triangle are 
and 
, compute the scalar projections of the sides AB and CB on AC, and check that their sum is equal to the length of AC.
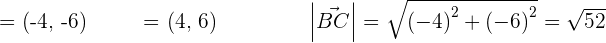
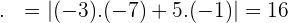
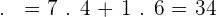
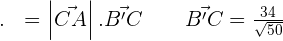
Find more Maths tutors here on Superprof.
Did you like this article? Rate it!
Loading...
