Chapters
- Exercise 1
- Exercise 2
- Exercise 3
- Exercise 4
- Exercise 5
- Exercise 6
- Exercise 7
- Exercise 8
- Exercise 9
- Solution of exercise 1
- Solution of exercise 2
- Solution of exercise 3
- Solution of exercise 4
- Solution of exercise 5
- Solution of exercise 6
- Solution of exercise 7
- Solution of exercise 8
- Solution of exercise 9

Exercise 1
Calculate the head of the vector  knowing that its components are
knowing that its components are 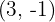 and its tail is
and its tail is 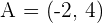 .
.
Exercise 2
Given points  and
and 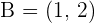 , calculate the value of a if the magnitude of the vector
, calculate the value of a if the magnitude of the vector  is one.
is one.
Exercise 3
Normalize the vectors: 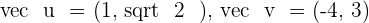 and
and  .
.
Exercise 4
Determine the unit vector,  , which is in the same direction as the vector
, which is in the same direction as the vector 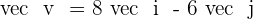 .
.
Exercise 5
Calculate the coordinates of D so that the quadrilateral formed by the vertices: 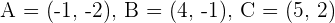 and D; is a parallelogram.
and D; is a parallelogram.
Exercise 6
The vectors  and
and  form a basis. Express this in basis the vector
form a basis. Express this in basis the vector 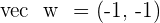 .
.
Exercise 7
Find the value of k so that the angle that forms between 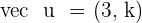 and
and 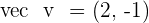 is:
is:
1 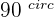
2 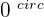
3 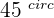
Exercise 8
Calculate the value of a so that the vectors 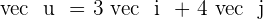 and
and 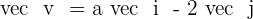 form an angle of
form an angle of 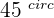 .
.
Exercise 9
If 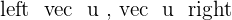 is an orthonormal basis, calculate:
is an orthonormal basis, calculate:
1 
2 
3 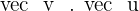
4 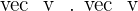
Solution of exercise 1
Calculate the head of the vector  knowing that its components are
knowing that its components are 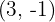 and its tail is
and its tail is 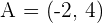 .
.
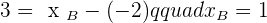
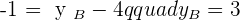

Solution of exercise 2
Given points  and
and 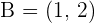 , calculate the value of a if the magnitude of the vector
, calculate the value of a if the magnitude of the vector  is one.
is one.


Solution of exercise 3
Normalize the vectors: 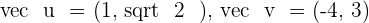 and
and  .
.

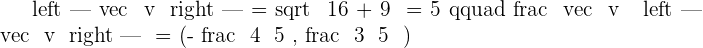
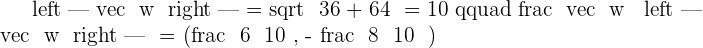
Solution of exercise 4
Determine the unit vector,  , which is in the same direction as the vector
, which is in the same direction as the vector 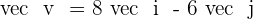 .
.
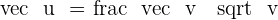
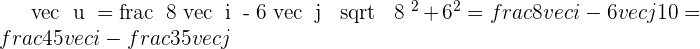
Solution of exercise 5
Calculate the coordinates of D so that the quadrilateral formed by the vertices: 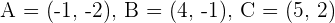 and D; is a parallelogram.
and D; is a parallelogram.
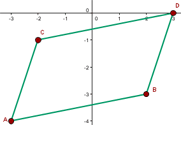
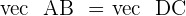


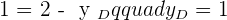
Hence, 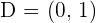
Solution of exercise 6
The vectors  and
and  form a basis. Express this in basis the vector
form a basis. Express this in basis the vector 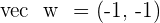 .
.

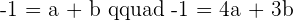

Replacing the value of a in the second equation:
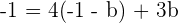

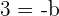

Plugging the value of b in the first equation:

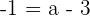


Solution of exercise 7
Find the value of k so that the angle that forms between 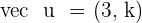 and
and 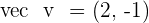 is:
is:
1 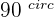


2 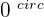


3 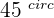

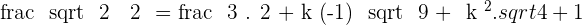
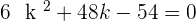
After solving the above equation:
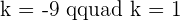
Solution of exercise 8
Calculate the value of a so that the vectors 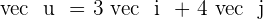 and
and 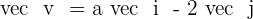 form an angle of
form an angle of 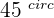 .
.
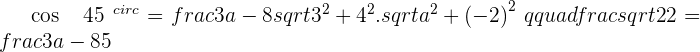

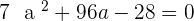
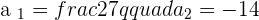
Solution of exercise 9
If 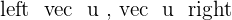 is an orthonormal basis, calculate:
is an orthonormal basis, calculate:
1 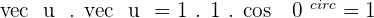
2 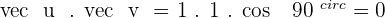
3 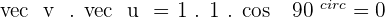
4 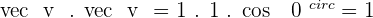
Find more Maths tutors here on Superprof.













