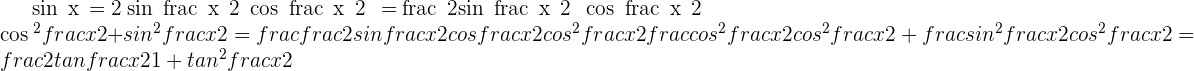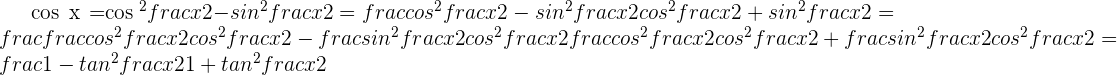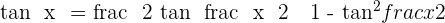Chapters
- Exercise 1
- Exercise 2
- Exercise 3
- Exercise 4
- Exercise 5
- Exercise 6
- Exercise 7
- Exercise 8
- Exercise 9
- Exercise 10
- Exercise 11
- Exercise 12
- Solution of exercise 1
- Solution of exercise 2
- Solution of exercise 3
- Solution of exercise 4
- Solution of exercise 5
- Solution of exercise 6
- Solution of exercise
- Solution of exercise 7
- Solution of exercise
- Solution of exercise 8
- Solution of exercise
- Solution of exercise 9
- Solution of exercise
- Solution of exercise 10
- Solution of exercise 11
- Solution of exercise 12
PS: Note that all the angles are in degree.

Exercise 1
Knowing that 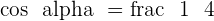 , and that
, and that 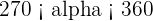 , calculate the remaining trigonometric ratios of angle
, calculate the remaining trigonometric ratios of angle 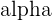 .
.
Exercise 2
Knowing that 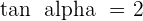 , and that
, and that 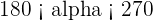 , calculate the remaining trigonometric ratios of angle
, calculate the remaining trigonometric ratios of angle 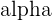 .
.
Exercise 3
Knowing that 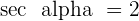 and
and 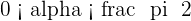 , calculate the remaining trigonometric ratios of angle
, calculate the remaining trigonometric ratios of angle 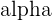 .
.
Exercise 4
Knowing that  , calculate the remaining trigonometric ratios of angle
, calculate the remaining trigonometric ratios of angle 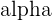 .
.
Exercise 5
Prove the identities:
1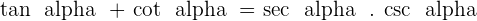
2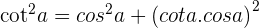
3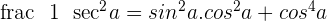
4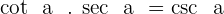
5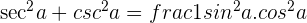
Exercise 6
Simplify the fractions:
1 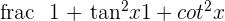
2 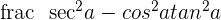
3 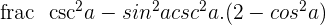
Exercise 7
Prove the identities:
Part 1
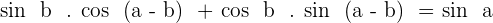
Part 2
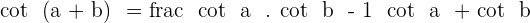
Exercise 8
Simplify the fractions:
Part 1
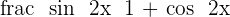
Part 2

Part 3
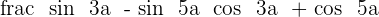
Exercise 9
Calculate the trigonometric ratios of  (from the
(from the  and
and  ).
).
Exercise 10
Develop:  .
.
Exercise 11
Calculate 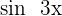 , depending on
, depending on 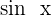 .
.
Exercise 12
Calculate 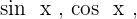 and
and 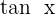 , in terms of
, in terms of  .
.
Solution of exercise 1
Knowing that 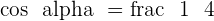 , and that
, and that 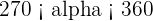 , calculate the remaining trigonometric ratios of angle
, calculate the remaining trigonometric ratios of angle 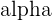 .
.
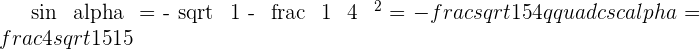

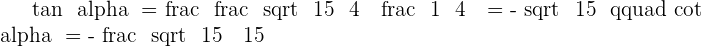
Solution of exercise 2
Knowing that 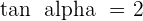 , and that
, and that 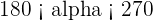 , calculate the remaining trigonometric ratios of angle
, calculate the remaining trigonometric ratios of angle 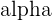 .
.
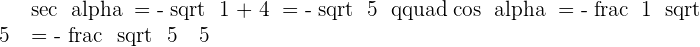
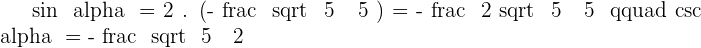
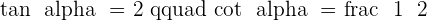
Solution of exercise 3
Knowing that 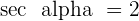 and
and 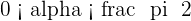 , calculate the remaining trigonometric ratios of angle
, calculate the remaining trigonometric ratios of angle 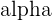 .
.
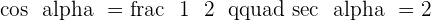
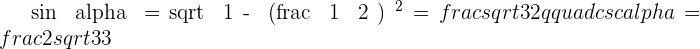
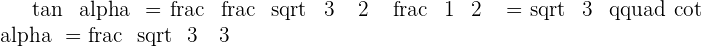
Solution of exercise 4
Knowing that  , calculate the remaining trigonometric ratios of angle
, calculate the remaining trigonometric ratios of angle 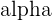 .
.
First quadrant:
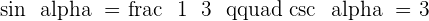
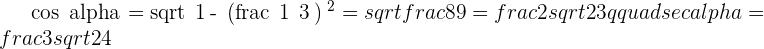
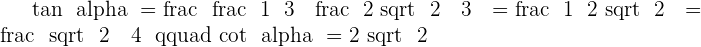
Second quadrant:
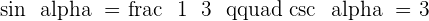

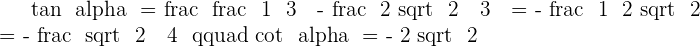
Solution of exercise 5
Prove the identities:
1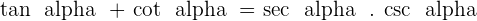
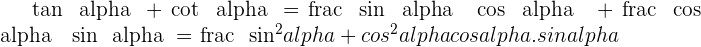

2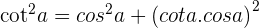
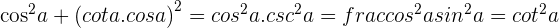
3

4
5
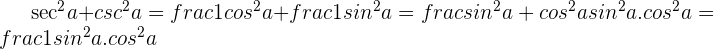
Solution of exercise 6
Simplify the fractions:
1 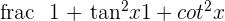
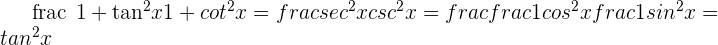
2 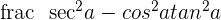
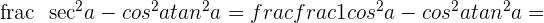

3 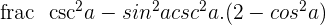
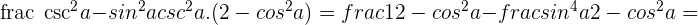

Solution of exercise
Solution of exercise 7
Prove the identities:
1 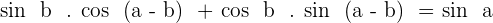

2 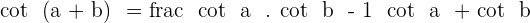
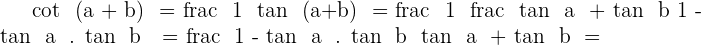
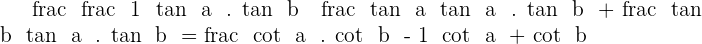
Solution of exercise
Solution of exercise 8
Simplify the fractions:
1 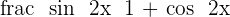

2 

3 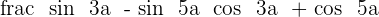
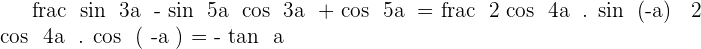
Solution of exercise
Solution of exercise 9
Calculate the trigonometric ratios of  (from the
(from the  and
and  ).
).
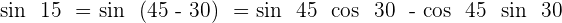


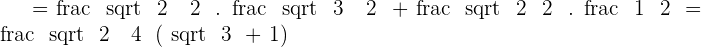
Solution of exercise
Solution of exercise 10
Develop:  .
.
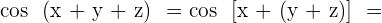
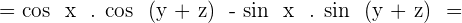
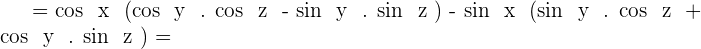

Solution of exercise 11
Calculate 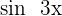 , depending on
, depending on 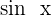 .
.
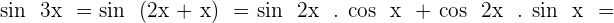

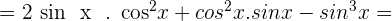
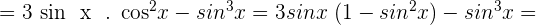
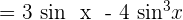
Solution of exercise 12
Calculate 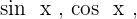 and
and 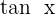 , in terms of
, in terms of  .
.