Chapters
In this article, we will discuss star polygons in detail. But before proceeding to discuss star polygons specifically, first, let us see what is a polygon.

What is a Polygon?
The word polygon is derived from two words: Poly means many and gon means sides. A polygon refers to a two-dimensional geometric figure that contains a finite number of sides. The straight line segments are used to make the sides of the polygon. These line segments are joined end to end and are also known as edges. The point in a polygon where two line segments meet each other is known as the corner or vertex of the polygon. The vertex is a point in a polygon where the angle is formed. Some examples of the polygon include square, rectangle, triangle, hectogon, and octagon, etc. A circle is not considered a polygon although it is a plane figure. This is because it has a curved shape and does not contain angles of sides. From this, we can conclude that all the polygons are 2D shapes, however, all two-dimensional figures are not polygons.
Now, let us see what are different types of polygon. These types are quite helpful in understanding star polygons.
Types of Polygon
Based on the angles and sides, a polygon is divided into four different types which are mentioned below:
- Irregular Polygon
- Regular Polygon
- Convex Polygon
- Concave polygon
Now, we will explain each of the above types in detail.
Irregular Polygon
An irregular polygon refers to a polygon in which all the sides and interior angles are of different measure. Examples of irregular polygons include a scalene triangle, a kite and a rectangle, etc. In all these figures, the sides and angles are of different measures.
Regular Polygon
A regular polygon refers to a type of polygon in which all the sides and interior angles are equal. In other words, we can say that a regular polygon is a geometrical figure which is not only equilateral but also equiangular. By equilateral, we mean that all the sides are of the same length and by equiangular we mean all the interior angles are of the same measure. Some examples of regular polygons include rhombus, equilateral triangle, and square, etc.
Convex Polygon
A convex polygon refers to a type of polygon in which all the interior angles are strictly less than 180 degrees. The vertex in these polygons will always point outwards from the center of their shape.
Concave Polygon
A concave polygon refers to a type of polygon in which one or more interior angles are greater than 180 degrees. There can be at least four sides in a concave polygon and the vertex of such polygons points towards inside the polygon.
In the next section, you will learn what is a star polygon.
What is a Star Polygon?
As we have already discussed above that a polygon is an enclosed figure that has a finite number of sides connected end to end. By this definition, a star can also be considered as a polygon as it is made up of several line segments known as sides of edges. These edges or sides are connected end to end with each other. A regular polygon is a type of polygon in which all sides are of the same length and the angles are also of the same measure. In geometry, a star polygon refers to a kind of non-convex polygon. Star polygons are usually not defined formally, however, regular star polygons are studied often.
A star polygon can be termed as a simple or complex polygon:
Simple polygon: A simple polygon refers to any enclosed figure that has straight, non-intersecting lines.
Complex polygon: A complex polygon refers to an enclosed figure which consists of straight lines that intersect
As we have already discussed above that a star polygon is also a type of convex polygon. A convex polygon refers to a polygon in which all the interior angles are less than 180 degrees. If it is not the case, then the polygon is referred to as a concave polygon.
Regular Star Polygon
Thomas Bradwardine first studied the geometry of regular star polygons. This geometry was later studied by Johannes Kepler. According to Kepler, a star polygon is an augmentation of a regular polygon, which is created by extending each side of a regular polygon until it creates a vertex by meeting a non-adjacent side. The formal definition of a regular star polygon is given below:
A self-intersecting equilateral and equiangular polygon is referred to as a regular star polygon.
By equilateral, we mean that all sides of a regular star polygon are of the same length. Equiangular means that all the angles of a regular star polygon are of the same measure.
A regular star polygon is constructed by joining nonconsecutive vertices of the regular convex polygons of continuous form. They are denoted by p/q, where p is the number of vertices of the convex regular polygon and q is the jump between vertices. Here, p/q must be an irreducible fraction (in reduced form). The polygon p/q is the same as the p/(p − q), as the polygon is obtained by joining vertices in a counterclockwise direction.
If we talk more precisely, then we can say that a regular star polygon can be constructed by joining one vertex of a simple, regular, p-sided polygon to another, non adjacent vertex. The process is continued until the original vertex is achieved again. It means that for integers p and q, a star polygon is created by joining every qth point out of p points, spaced uniformly in a circular placement.
How Star Polygons are Constructed?
To create a star polygon with p vertices, we subdivide the circle into p points that are uniformly paced to create congruent arcs. Then, we start joining the vertices. Starting from the initial vertex, we connect it to another vertex which is present q positions from it. The numbers p and q are prime numbers and the points joined are segregated by at least one point.
Some figures depicting a regular star polygon are given below:
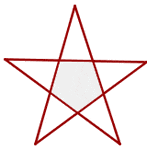
Regular Star Pentagon
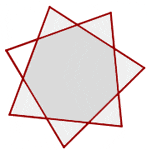
Regular Star Heptagons
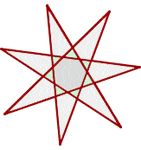

Regular Star Octagon
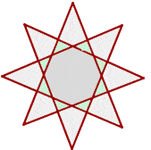
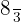
Regular Star Enneagons


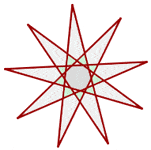
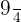
Regular Star Decagon
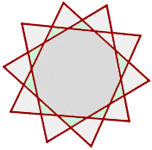
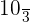













I’m just curious if the area between the polygon and the circumscribed circle has a name.
https://www.superprof.co.uk/resources/academic/maths/geometry/plane/orthocenter-centroid-circumcenter-and-incenter-of-a-triangle.html