Chapters

Introduction to Polygons
In this article, we will discuss the angles of polygons in detail. But before discussing the angles, first, let us see what are polygons.
The word polygon is made up of two words: Poly and gon. Poly means many and gon means sides. A polygon is a geometrical figure that has many sides. At least three line segments are required to make a polygon. We can define a polygon as:
A 2D geometric figure that contains a finite number of sites is known as a polygon.
The sides of the polygon are composed of straight line segments that are joined end to end with each other. These straight line segments are referred to as sides or edges of a polygon. The points where the line segments meet each other are corners or vertices of the polygon. A polygon may have three or more vertices. The angles are formed when line segments meet each other. A triangle is the best example of a polygon with three sides, three vertices, and three angles.
A circle is also a geometrical figure but we cannot say that it is a polygon because it does not contain sides, vertices, or angles. Rather, it is a curved geometrical figure. This helps us to conclude the fact that all the polygons regardless of their sides or vertices are two-dimensional figures, however, all two-dimensional figures are not polygons. Some other examples of a polygon are square, quadrilateral, pentagon, hexagon, and octagon.
Properties
Based on the angles and sides, the polygons exhibit the following properties:
- The sum of all the interior angles of a polygon with 'n' number of sides is equal to
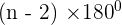 .
. - The number of diagonals in a polygon with 'n' number of sides is given by the formula

- The number of triangles that are created by connecting the diagonals from one corner of the polygon can be calculated by n - 2, where 'n' represents the number of sides of a polygon
- The measure of the interior angle of a regular polygon with 'n' number of sides is given by
 .
. - The measure of each exterior angle of a polygon having 'n' number of sides is given by
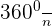
Types of Polygon
Based on the angles and sides, the polygons are divided into the following four types:
- Irregular polygon
- Regular polygon
- Concave polygon
- Convex polygon
Irregular Polygon
If the measure of sides and interior angles of a polygon are different, then the polygon is referred to as an irregular polygon. Examples of irregular polygons include a kite, rectangle, and scalene triangle.
Regular Polygon
A regular polygon is a polygon in which all the sides and interior angles are of the same measure. Examples of regular polygons include rhombus, equilateral triangle, and square, etc.
Convex Polygon
A convex polygon refers to a polygon in which all the interior angles are less than 180 degrees. The vertex of these polygons always points outwards from the center of their shapes.
Concave Polygon
A concave polygon is a polygon in which one or more interior angles are more than 180 degrees. This type of polygon can have at least four sides and the vertex points are towards the inside of the polygon.
In the next section of the article, we will discuss the angles of polygons in detail.
Angles of Polygons
Interior Angles
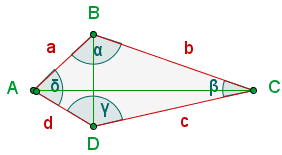
An interior angle or internal angle is determined by two consecutive sides. In the figure below,  ,
,  ,
,  , and
, and  are four angles.
are four angles.
Sum of Interior Angles of a Polygon
The interior angle of a polygon is given by the formula 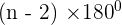 . We can also say that sum is equal to
. We can also say that sum is equal to 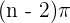 radians. Here, 'n' refers to the number of sides of a polygon.
radians. Here, 'n' refers to the number of sides of a polygon.
For instance, a quadrilateral is a four sided polygon. The sum of interior angles of a quadrilateral is given by:
Sum of interior angles of a quadrilateral = 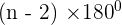
=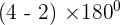
= 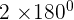
= 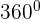
By using the above formula, we can also calculate the sum of interior angles of other polygons such as a triangle, pentagon, hexagon, and octagon.
Sum of interior angles of a triangle = (3 − 2) · 180° = 180º.
Sum of interior angles of a pentagon = (5 − 2) · 180° = 540º.
Sum of interior angles of a hexagon = (5 − 2) · 180° = 720º.
Sum of interior angles of a hexagon = (8 − 2) · 180° = 1080º.
Exterior angle
The aggregate of interior and the corresponding exterior angles at each vertex of any type of polygon are supplementary to each other, i.e., they add up to 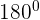 . In the figure below, you can see the exterior angle of the pentagon:
. In the figure below, you can see the exterior angle of the pentagon:
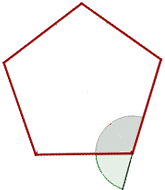
Hence, we can conclude that:
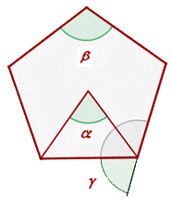
Interior angle + Exterior angle = 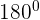
Exterior angle = 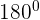 - Interior angle
- Interior angle
Angles of a Regular Polygon
Central Angle of a Regular Polygon
We know that a regular polygon is a polygon in which the measure of angles and sides are equal. The central angle of a regular polygon is created by two lines from consecutive vertices to the center point or two radii of consecutive vertices of the circumscribed circle. A central angle  in a regular five sided polygon is shown in the figure below:
in a regular five sided polygon is shown in the figure below:
The central angle of a polygon is given by the following formula:
Central angle = 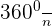 , where n is the number of sides of a polygon
, where n is the number of sides of a polygon
Consider the following example:
What is the measure of the central angle of a hexagon?
A hexagon is a six sided polygon. We can simply substitute n = 6 in the formula 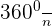 to get the central angle of hexagon:
to get the central angle of hexagon:
Central angle = 
Interior Angle of a Regular Polygon
The interior angle of a regular polygon is formed by two consecutive sides. The interior angle in a regular five sided polygon, i.e. a pentagon is shown in the figure below:

Interior angle = 180° − central angle
We already have calculated the central angle of a pentagon which is equal to  . From this, we can now find the measure of the interior angle of hexagon:
. From this, we can now find the measure of the interior angle of hexagon:
Interior angle of a regular hexagon = 180° − 60º = 120º
Exterior Angle of a Regular Polygon
The exterior angle of a regular polygon is formed by one side and the extension of the consecutive side.
The exterior and interior angles are supplementary to each other, that is to say, that adds up 180º.
Exterior angle + Interior angle = 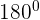
The exterior angle of a regular polygon is equal to its central angle.
Exterior angle = central angle
Exterior angle of the regular hexagon = 60º.













I’m just curious if the area between the polygon and the circumscribed circle has a name.
https://www.superprof.co.uk/resources/academic/maths/geometry/plane/orthocenter-centroid-circumcenter-and-incenter-of-a-triangle.html