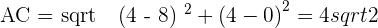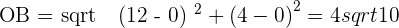Chapters
- Exercise 1
- Exercise 2
- Exercise 3
- Exercise 4
- Exercise 5
- Exercise 6
- Exercise 7
- Exercise 8
- Exercise 9
- Solution of exercise 1
- Solution of exercise 2
- Solution of exercise 3
- Solution of exercise 4
- Solution of exercise 5
- Solution of exercise 6
- Solution of exercise 7
- Solution of exercise 8
- Solution of exercise 9

Exercise 1
Write the equation (in all possible forms) of the line that passes through the points 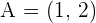 and
and 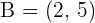 .
.
Exercise 2
Identify the type of triangle formed by the points: 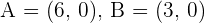 and
and  .
.
Exercise 3
Determine the slope and y-intercept of the line 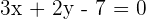 .
.
Exercise 4
Find the equation of the line r which passes through the point 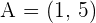 and is parallel to the line
and is parallel to the line  .
.
Exercise 5
Find the equation of the line that passes through the point  and is parallel to the straight line that joins the points
and is parallel to the straight line that joins the points  and
and  .
.
Exercise 6
The points 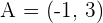 and
and 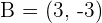 are vertices of an isosceles triangle ABC that has its apex C on the line
are vertices of an isosceles triangle ABC that has its apex C on the line  . If AC and BC are the equal sides, calculate the coordinates of Point C.
. If AC and BC are the equal sides, calculate the coordinates of Point C.
Exercise 7
The line 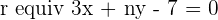 passes through the point
passes through the point  and is parallel to the line
and is parallel to the line 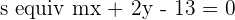 . Calculate the values of m and n.
. Calculate the values of m and n.
Exercise 8
Given triangle ABC with coordinates  and
and 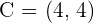 , calculate the equation of the median that passes through the vertex C.
, calculate the equation of the median that passes through the vertex C.
Exercise 9
A parallelogram has a vertex 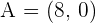 , and the point of intersection of its two diagonals is
, and the point of intersection of its two diagonals is  . If the other vertex is at the origin, calculate:
. If the other vertex is at the origin, calculate:
1 The other two vertices.
2 The equations of the diagonals.
3 The length of the diagonal.
Solution of exercise 1
Write the equation (in all possible forms) of the line that passes through the points 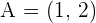 and
and 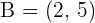 .
.
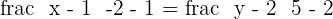
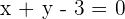
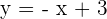

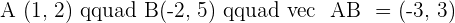

Solution of exercise 2
Identify the type of triangle formed by the points: 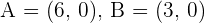 and
and  .
.
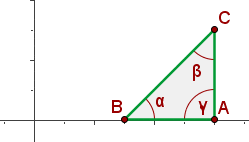
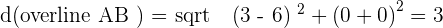
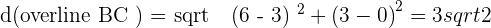
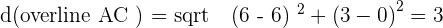
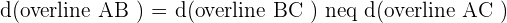 Isosceles
Isosceles
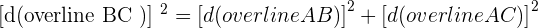 Right triangle
Right triangle
Solution of exercise 3
Determine the slope and y-intercept of the line 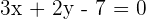 .
.


Solution of exercise 4
Find the equation of the line r which passes through the point 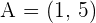 and is parallel to the line
and is parallel to the line  .
.
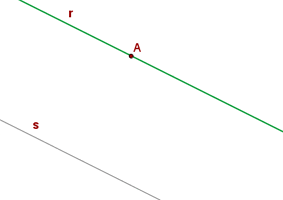
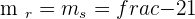
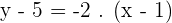
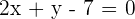
Solution of exercise 5
Find the equation of the line that passes through the point  and is parallel to the straight line that joins the points
and is parallel to the straight line that joins the points  and
and  .
.

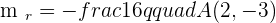

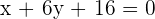
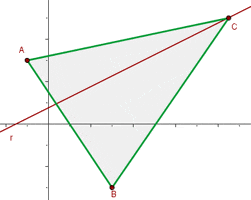
Solution of exercise 6
The points 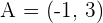 and
and 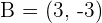 are vertices of an isosceles triangle ABC that has its apex C on the line
are vertices of an isosceles triangle ABC that has its apex C on the line  . If AC and BC are the equal sides, calculate the coordinates of Point C.
. If AC and BC are the equal sides, calculate the coordinates of Point C.
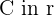
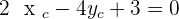
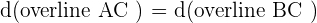
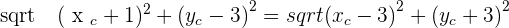
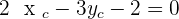
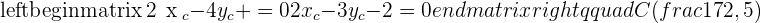
Solution of exercise 7
The line 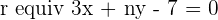 passes through the point
passes through the point  and is parallel to the line
and is parallel to the line 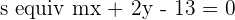 . Calculate the values of m and n.
. Calculate the values of m and n.

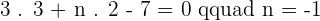

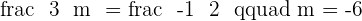
Solution of exercise 8
Given triangle ABC with coordinates  and
and 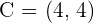 , calculate the equation of the median that passes through the vertex C.
, calculate the equation of the median that passes through the vertex C.



Solution of exercise 9
A parallelogram has a vertex 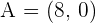 , and the point of intersection of its two diagonals is
, and the point of intersection of its two diagonals is  . If the other vertex is at the origin, calculate:
. If the other vertex is at the origin, calculate:
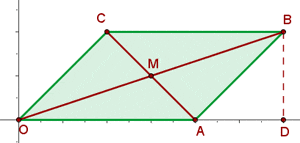
1 The other two vertices.
M is the midpoint of 
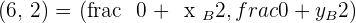

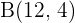
M is the midpoint of 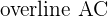
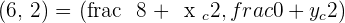
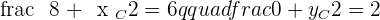

2 The equations of the diagonals.
Equation of AC
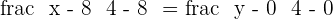
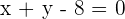
Equation of OB
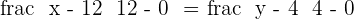
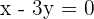
3 The length of the diagonal.