Chapters
- Exercise 1
- Exercise 2
- Exercise 3
- Exercise 4
- Exercise 5
- Exercise 6
- Exercise 7
- Exercise 8
- Exercise 9
- Exercise 10
- Exercise 11
- Exercise 12
- Solution of exercise 1
- Solution of exercise 2
- Solution of exercise 3
- Solution of exercise 4
- Solution of exercise 5
- Solution of exercise 6
- Solution of exercise 7
- Solution of exercise 8
- Solution of exercise 9
- Solution of exercise 10
- Solution of exercise 11
- Solution of exercise 12

Exercise 1
Calculate the center coordinates and radius of the following circles, if applicable:
Exercise 2
Calculate the equation of the circle that has its center at (2, −3) and has the x-axis as a tangent.
Exercise 3
Calculate the equation of the circle that has its center at (−1, 4) and has the y-axis as a tangent.
Exercise 4
Calculate the equation of the circle which is centered at the point of intersection of the lines  and
and  and its radius is equal to 5.
and its radius is equal to 5.
Exercise 5
Find the equation of the circle which is concentric to the circle with equation 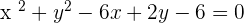 , and passes through the point (−3, 4).
, and passes through the point (−3, 4).
Exercise 6
A triangle with vertices A = (0, 0), B = (3, 1) and C = (5, 7) is inscribed in a circle. Calculate the equation of this circle.
Exercise 7
The ends of the diameter of a circle are the points A = (−5, 3) and B = (3, 1). What is the equation of this circle?
Exercise 8
Find the equation of the concentric circle to the circle  which has a tangent of
which has a tangent of 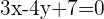 .
.
Exercise 9
Determine the points of intersection for the circle 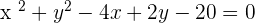 with the following lines:
with the following lines:
Exercise 10
Determine the equation of the circle which has its center at C = (3, 1) and a tangent of  .
.
Exercise 11
Find the equation of the circle that passes through the points A = (2, 1) and B = (−2, 3) and has its center on the line: 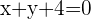 .
.
Exercise 12
Calculate the equation of the circle that passes through the point (0, −3), whose radius is  and whose center is on the angle bisector of the first and third quadrants.
and whose center is on the angle bisector of the first and third quadrants.
Solution of exercise 1
Calculate the center coordinates and radius of the following circles, if applicable:
1. 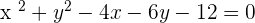
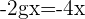 , therefore,
, therefore, 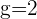
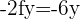 , therefore,
, therefore, 
Hence, C=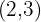
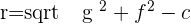

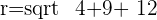
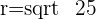
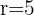
2. 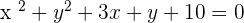
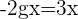 , therefore,
, therefore, 
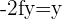 , therefore,
, therefore, 
Hence, C=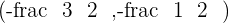
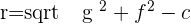
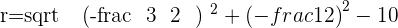
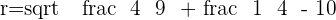
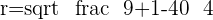
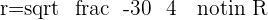
It is not a circle.
3. 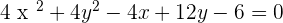
Dividing the whole equation by 4:
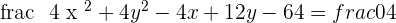
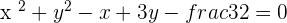
 , therefore,
, therefore, 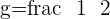
 , therefore,
, therefore, 
Hence, C=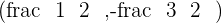
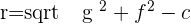
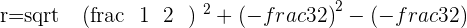

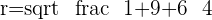



Solution of exercise 2
Calculate the equation of the circle that has its center at (2, −3) and has the x-axis as a tangent.

In this question, the circle has an x-axis as a tangent. A tangent is a straight line that touches a curve. This means that the "y coordinate" will be zero. We will use the distance formula to find the radius. Currently, we have 2 coordinates which are: C(2,-3), T(2,0)
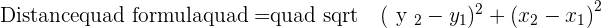
Plugging the values of C and T:
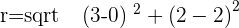
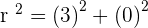
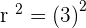
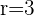
Since we know the value of the radius and center of the circle, the equation will be:
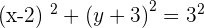
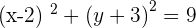
Solution of exercise 3
Calculate the equation of the circle that has its center at (−1, 4) and has the y-axis as a tangent.
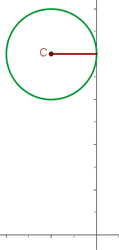
This time, the circle has the y-axis as a tangent. This means that the x coordinate will be zero. Hence, we have 2 coordinates which are C(-1,4) and T(0,4). We will use the distance formula again to find the value of the radius.
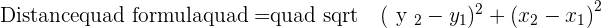
Plugging the values of C and T:

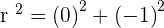
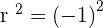
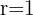
Since we know the value of the radius and center of the circle, the equation will be:
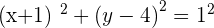
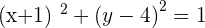
Solution of exercise 4
Calculate the equation of the circle which is centered at the point of intersection of the lines  and
and  and its radius is equal to 5.
and its radius is equal to 5.
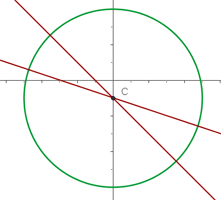

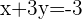 ->Equation 1
->Equation 1

 ->Equation 2
->Equation 2
Now both equations will be solved simultaneously to find the value of x and y. The value of x and y will be the coordinate of the center of the circle. After solving simultaneously, the center of the circle will be C=(0,-1).

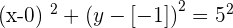
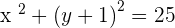
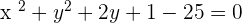
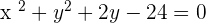
There is another method to solve this question. However, you still need to find the center by solving the linear equations simultaneously. Below is another method to find the equation of the circle.
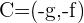
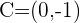
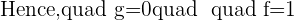


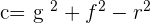
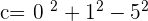
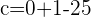
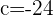


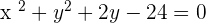
Solution of exercise 5
Find the equation of the circle which is concentric to the circle with equation 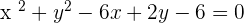 , and passes through the point (−3, 4).
, and passes through the point (−3, 4).
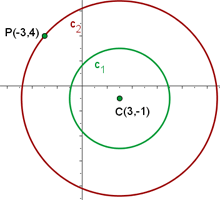
We will find the center of the circle from 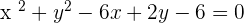 and then we will find the radius with the help of distance formula. In the end, we will put all the values in the general equation or standard equation to find the equation of the circle.
and then we will find the radius with the help of distance formula. In the end, we will put all the values in the general equation or standard equation to find the equation of the circle.
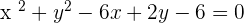

Compairing the above equations to find the value of g and f:
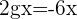
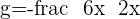
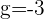
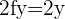
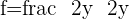


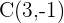
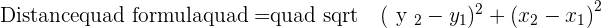
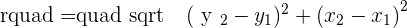
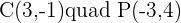
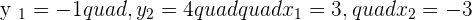
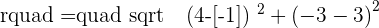

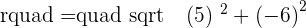

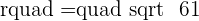

Putting the values of a, b, and r:
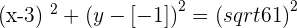
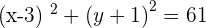
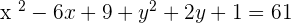
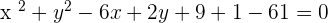
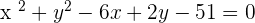
Finding the equation of the circle by using the standard equation:
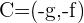




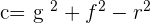
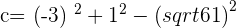
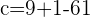
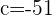

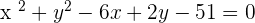
Solution of exercise 6
A triangle with vertices A = (0, 0), B = (3, 1) and C = (5, 7) is inscribed in a circle. Calculate the equation of this circle.

We will insert all the coordinates in the standard equation to find the value of g, f, and c. Once we find the values of g,f, and c then we will insert all those values in the standard equation to develop the equation of the circle.
Standard Equation= 
Plugging the coordinates of A:
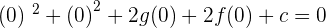
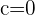
Plugging the coordinates of B:
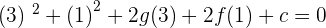
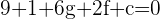
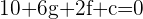
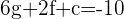
Plugging the coordinates of C:



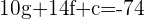
After solving the above equations, we will get:
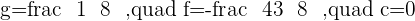
Putting all the values in the general equation of the circle:

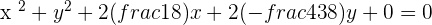
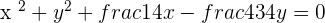
Solution of exercise 7
The ends of the diameter of a circle are the points A = (−5, 3) and B = (3, 1). What is the equation of this circle?

We will find the diameter with the help of the distance formula. To find the radius, we will divide the diameter into half. Furthermore, if we find the midpoint of the AB line, that will be the center of the circle. We will use the midpoint formula to find the coordinates of the center of the circle.
Finding the diameter:
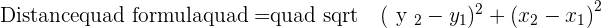
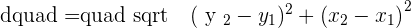
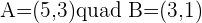

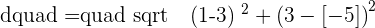



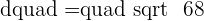
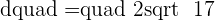
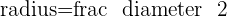

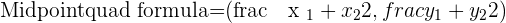

Since, midpoint is the center of the circle, therefore, we will declare midpoint as the center of the circle:


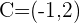
Plugging the value of C and r in the standard equation:
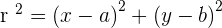
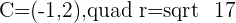
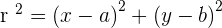


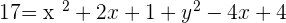
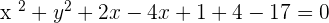
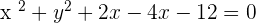
You can also find the equation from the general equation of the circle:
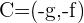
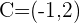
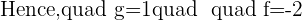


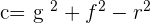
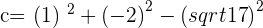

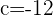
Plugging all the values of the g, f, and c in the general equation:

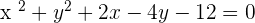
Find various Maths tutors on Superprof.
Solution of exercise 8
Find the equation of the concentric circle to the circle  which has a tangent of
which has a tangent of 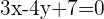 .
.



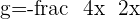
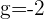



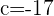

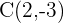
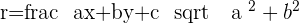

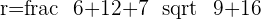
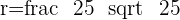

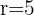


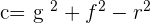
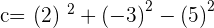

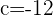
Plugging all the values in the general equation:

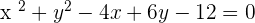
Solution of exercise 9
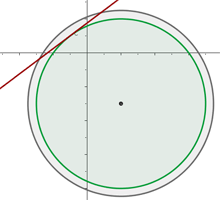
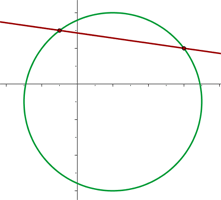
Determine the points of intersection for the circle 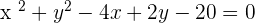 with the following lines:
with the following lines:
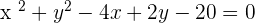 -> Equation 1
-> Equation 1
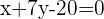 -> Equation 2
-> Equation 2
After solving the above equations simultaneously, we will get:
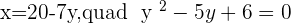

The factors of the above equation will be: 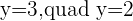
Putting the values of y in the x equation to find values of x:
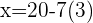


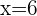
So our coordinates are: 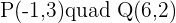
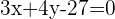

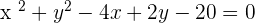 -> Equation 1
-> Equation 1
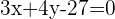 -> Equation 2
-> Equation 2
After solving the above equations simultaneously, we will get:

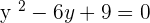
The factor of the above equation will be: 
Putting the values of y in the x equation to find values of x:
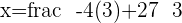
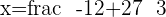
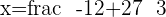
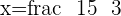

So our coordinate are: 
3. 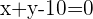

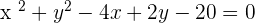 -> Equation 1
-> Equation 1
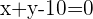 -> Equation 2
-> Equation 2
After solving the above equations simultaneously, we will get:
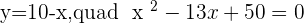
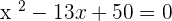
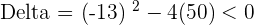
Solution of exercise 10
Determine the equation of the circle which has its center at C = (3, 1) and a tangent of  .
.
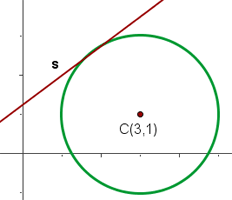
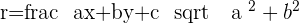
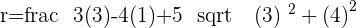
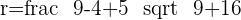
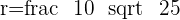
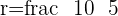

Since we know the coordinate of the center of the circle and value of the radius, therefore, we can create the equation of the circle:

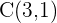
Hence, 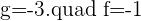


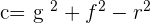
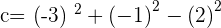

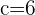
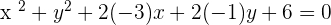
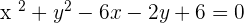
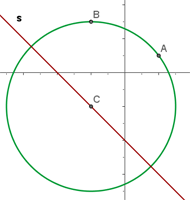
Solution of exercise 11
Find the equation of the circle that passes through the points A = (2, 1) and B = (−2, 3) and has its center on the line: 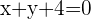 .
.
Plugging the coordinates of A in the standard equation:


Since both radii are the same, therefore:
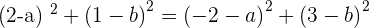 -> Equation 1
-> Equation 1
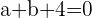 -> Equation 2
-> Equation 2
After solving the above equations simultaneously, we will get: 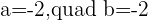
Plugging the value of a and b in the standard equation to find the radius:
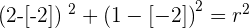
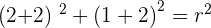
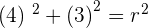
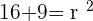
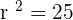
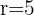
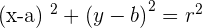
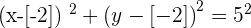


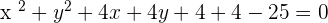

Solution of exercise 12
Calculate the equation of the circle that passes through the point (0, −3), whose radius is  and whose center is on the angle bisector of the first and third quadrants.
and whose center is on the angle bisector of the first and third quadrants.
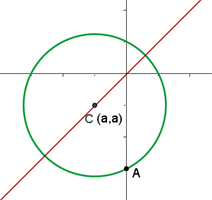
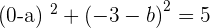


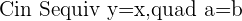

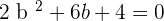


For b=-1:
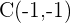 ,
, 
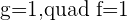


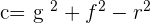

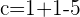
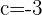

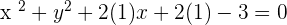
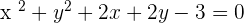
For b=-2:
 ,
, 
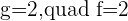
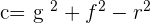
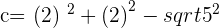
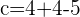
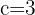

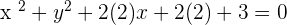
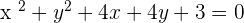













It is clear and understandable .
thankyouuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuu
This is very nice but please show how to find the 4p