Chapters
- Exercise 1
- Exercise 2
- Exercise 3
- Exercise 4
- Exercise 5
- Exercise 6
- Exercise 7
- Exercise 8
- Exercise 9
- Solution of exercise 1
- Solution of exercise 2
- Solution of exercise 3
- Solution of exercise 4
- Solution of exercise 5
- Solution of exercise 6
- Solution of exercise 7
- Solution of exercise 8
- Solution of exercise 9

Exercise 1
Determine the equations of the following parabolas and indicate the values of their focal parameter, focus and directrix.
1 
2 
Exercise 2
Determine the equations of the parabolas using the information given:
1 The directrix is x = −3 and the focus is (3, 0).
2 The directrix is y = 4 and the vertex is (0, 0).
3 The directrix is y = −5 and the focus is (0, 5).
4 The directrix is x = 2 and the focus is (−2, 0).
5 The focus is (2, 0) and the vertex is (0, 0).
6 The focus is (3, 2) and the vertex is (5, 2).
7 The focus is (−2, 5) and the vertex is (−2, 2).
8 The focus is (3, 4) and the vertex is (1, 4).
Exercise 3
Calculate the vertex, focus and directrix of the following parabolas:
1 
2 
3 
Exercise 4
Find the equation of the vertical parabola that passes through the points: A = (6, 1), B = (−2, 3) and C = (16, 6).
Exercise 5
Determine the equation of the parabola with a directrix of y = 0 and a focus at (2, 4).
Exercise 6
Determine the point(s) of intersection between the line r ≡ x + y − 5 = 0 and the parabola y² = 16x.
Exercise 7
Find the equation of the horizontal parabola that passes through the point (3, 4) and has its vertex at (0, 0).
Exercise 8
Determine the equation of the parabola with an axis parallel to the y-axis, vertex on the x-axis and which passes through the points A = (2, 3) and B = (−1, 12).
Exercise 9
Determine the equation of the parabola with a directrix of x + y − 6 = 0 and a focus at (0, 0).
Solution of exercise 1
Determine the equations of the following parabolas and indicate the values of their focal parameter, focus and directrix.
1 







2 



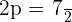



3 







Solution of exercise 2
Determine the equations of the parabolas using the information given:
1 The directrix is x = −3 and the focus is (3, 0).



2 The directrix is y = 4 and the vertex is (0, 0).



3 The directrix is y = −5 and the focus is (0, 5).



4 The directrix is x = 2 and the focus is (−2, 0).



5 The focus is (2, 0) and the vertex is (0, 0).



6 The focus is (3, 2) and the vertex is (5, 2).



7 The focus is (−2, 5) and the vertex is (−2, 2).



8 The focus is (3, 4) and the vertex is (1, 4).


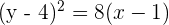
Solution of exercise 3
Calculate the vertex, focus and directrix of the following parabolas:
1 











2 











3 

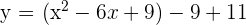









Solution of exercise 4
Find the equation of the vertical parabola that passes through the points: A = (6, 1), B = (−2, 3) and C = (16, 6).








Solution of exercise 5
Determine the equation of the parabola with a directrix of y = 0 and a focus at (2, 4).




Find various Maths tutor on Superprof.
Solution of exercise 6
Determine the point(s) of intersection between the line r ≡ x + y − 5 = 0 and the parabola y² = 16x.








Solution of exercise 7
Find the equation of the horizontal parabola that passes through the point (3, 4) and has its vertex at (0, 0).




Solution of exercise 8
Determine the equation of the parabola with an axis parallel to the y-axis, vertex on the x-axis and which passes through the points A = (2, 3) and B = (−1, 12).
Axis parallel to the y-axis 
Vertex on the x-axis 








Solution of exercise 9
Determine the equation of the parabola with a directrix of x + y − 6 = 0 and a focus at (0, 0).
















It is clear and understandable .
thankyouuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuu
This is very nice but please show how to find the 4p