Chapters
- Exercise 1
- Exercise 2
- Exercise 3
- Exercise 4
- Exercise 5
- Exercise 6
- Exercise 7
- Exercise 8
- Exercise 9
- Exercise 10
- Exercise 11
- Exercise 12
- Exercise 13
- Solution of exercise 1
- Solution of exercise 2
- Solution of exercise 3
- Solution of exercise 4
- Solution of exercise 5
- Solution of exercise 6
- Solution of exercise 7
- Solution of exercise 8
- Solution of exercise 9
- Solution of exercise 10
- Solution of exercise 11
- Solution of exercise 12
- Solution of exercise 13

Exercise 1
Determine and plot the coordinates of the foci and vertices and calculate the eccentricity of the following hyperbolas:
1 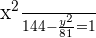
2 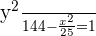
3 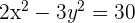
4 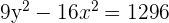
Exercise 2
Determine and plot the coordinates of the foci and vertices and calculate the eccentricity of the following hyperbolas:
1 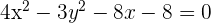
2 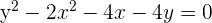
Exercise 3
Calculate the equation of the hyperbola with a transverse axis of 8 and a focal length of 10.
Exercise 4
The transverse axis of a hyperbola is 12 and the curve passes through the point P = (8, 14). Find its equation.
Exercise 5
Calculate the equation of the hyperbola centered at (0, 0) whose focal length is 34 and the distance from one focus to the closest vertex is 2.
Exercise 6
Determine the equation of the hyperbola centered at (0, 0) that passes through the points: 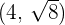 and
and  . .
. .
Exercise 7
Determine the equation of the hyperbola centered at (0, 0) that passes through the point  and whose eccentricity is
and whose eccentricity is 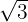 .
.
Exercise 8
Determine the equation of the hyperbola centered at (0, 0) knowing that one focus is 2 units from one vertex and 50 from the other.
Exercise 9
Determine the coordinates of the point(s) of intersection between the line x + y − 1 = 0 and the hyperbola  .
.
Exercise 10
A rectangular hyperbola passes through the point  . Find its equation and determine the coordinates of the vertices and foci.
. Find its equation and determine the coordinates of the vertices and foci.
Exercise 11
The transverse axis of a hyperbola is 12 and the eccentricity is 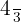 . Calculate the equation of this hyperbola.
. Calculate the equation of this hyperbola.
Exercise 12
Calculate the equation of a rectangular hyperbola knowing that its focal length is  .
.
Exercise 13
The length of the conjugate axis of a hyperbola is 8 and the equations of the asymptotes are:  . . Calculate the equation of the hyperbola, its foci and vertices.
. . Calculate the equation of the hyperbola, its foci and vertices.
Solution of exercise 1
Determine and plot the coordinates of the foci and vertices and calculate the eccentricity of the following hyperbolas:
1 
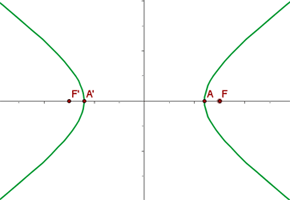
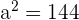

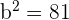

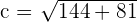
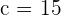
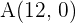

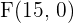
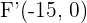

2 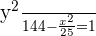
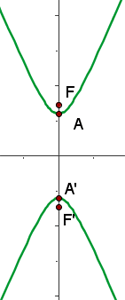
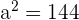


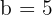
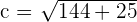
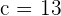

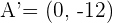
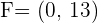


3 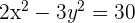
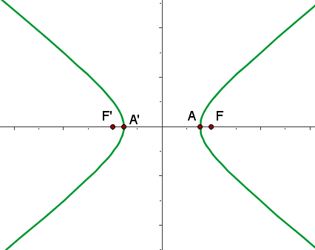
Divide by 30:

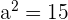
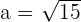

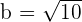


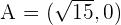
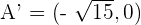
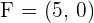


4 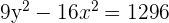

Divide by 1296:

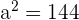

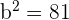

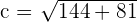
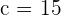
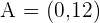
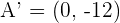
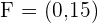

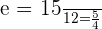
Solution of exercise 2
Determine and plot the coordinates of the foci and vertices and calculate the eccentricity of the following hyperbolas:
1 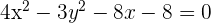
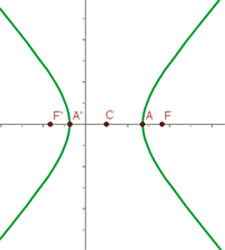
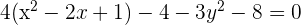
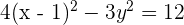



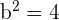




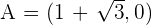
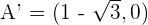
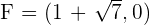
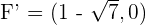
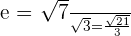
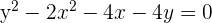

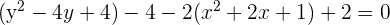


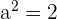
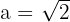
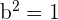


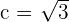
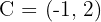

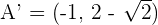
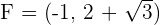
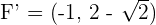

Solution of exercise 3
Calculate the equation of the hyperbola with a transverse axis of 8 and a focal length of 10.
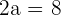
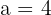
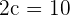




Solution of exercise 4
The transverse axis of a hyperbola is 12 and the curve passes through the point P = (8, 14). Find its equation.
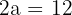



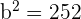

Solution of exercise 5
Calculate the equation of the hyperbola centered at (0, 0) whose focal length is 34 and the distance from one focus to the closest vertex is 2.
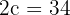
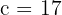
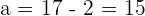
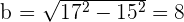

Solution of exercise 6
Determine the equation of the hyperbola centered at (0, 0) that passes through the points: 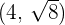 and
and  .
.

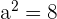
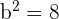

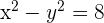
Solution of exercise 7
Determine the equation of the hyperbola centered at (0, 0) that passes through the point  and whose eccentricity is
and whose eccentricity is 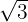 .
.

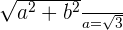
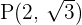

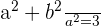
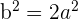





Solution of exercise 8
Determine the equation of the hyperbola centered at (0, 0) knowing that one focus is 2 units from one vertex and 50 from the other.
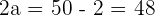
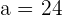
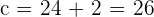
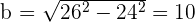

Solution of exercise 9
Determine the coordinates of the point(s) of intersection between the line x + y − 1 = 0 and the hyperbola x² - 2y²= 1.

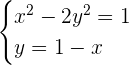

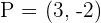
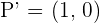
Solution of exercise 10
A rectangular hyperbola passes through the point (4, 1/2). Find its equation and determine the coordinates of the vertices and foci.
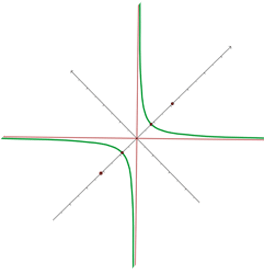


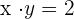
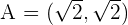
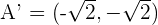

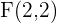
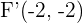
Solution of exercise 11
The transverse axis of a hyperbola is 12 and the eccentricity is 4/3. Calculate the equation of this hyperbola.
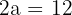


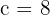
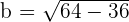


Solution of exercise 12
Calculate the equation of a rectangular hyperbola knowing that its focal length is  /
/ 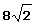



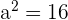



Find various Maths tutor on Superprof.
Solution of exercise 13
The length of the conjugate axis of a hyperbola is 8 and the equations of the asymptotes are:  . Calculate the equation of the hyperbola, its foci and vertices.
. Calculate the equation of the hyperbola, its foci and vertices.



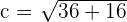



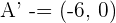

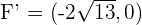













It is clear and understandable .
thankyouuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuu
This is very nice but please show how to find the 4p