Chapters
- Exercise 1
- Exercise 2
- Exercise 3
- Exercise 4
- Exercise 5
- Exercise 6
- Exercise 7
- Exercise 8
- Exercise 9
- Exercise 10
- Exercise 11
- Solution of exercise 1
- Solution of exercise 2
- Solution of exercise 3
- Solution of exercise 4
- Solution of exercise 5
- Solution of exercise 6
- Solution of exercise 7
- Solution of exercise 8
- Solution of exercise 9
- Solution of exercise 10
- Solution of exercise 11

Exercise 1
Calculate and plot the coordinates of the foci and vertices and determine the eccentricity of the following ellipses:
1 
2 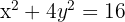
3 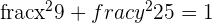
4 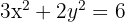
Exercise 2
Calculate and plot the coordinates of the foci and vertices and determine the eccentricity of the following ellipses:
1 
2 
3 
4 
Exercise 3
Determine the equations of the following ellipses using the information given:
1 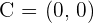 ,
, 

2 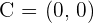 ,
, 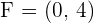

3  ,
, 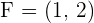
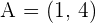
4  ,
, 

Exercise 4
Determine the equation of the ellipse that is centered at (0, 0), passes through the point (2, 1) and whose minor axis is 4.
Exercise 5
The focal length of an ellipse is 4 and the distance from a point on the ellipse is 2 and 6 units from each foci respectively. Calculate the equation of the ellipse if it is centered at (0, 0).
Exercise 6
Determine the equation of the ellipse which is centered at (0, 0) and passes through the points:
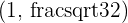 and
and  .
.
Exercise 7
Find the coordinates of the midpoint of the chord in the line: x + 2y − 1 = 0 which intersects the ellipse: x² + 2y² = 3.
Exercise 8
Determine the equation of the ellipse centered at (0, 0) whose focal length is  and the area of a rectangle in which the ellipse is inscribed within is 80 u².
and the area of a rectangle in which the ellipse is inscribed within is 80 u².
Exercise 9
Find the equation of the locus of points P (x, y) whose sum of distances to the fixed points (4, 2) and (−2, 2) is equal to 8.
Exercise 10
Determine the equation of the ellipse centered at (0, 0) knowing that one of its vertices is 8 units from a focus and 18 from the other.
Exercise 11
Determine the equation of the ellipse centered at (0, 0) knowing that it passes through the point (0, 4) and its eccentricity is 3/5.
Check out various Maths tutor near me on Superprof.
Solution of exercise 1
Calculate and plot the coordinates of the foci and vertices and determine the eccentricity of the following ellipses:
1 
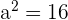
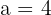
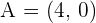
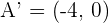
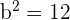

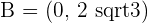
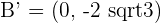


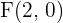
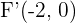
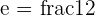
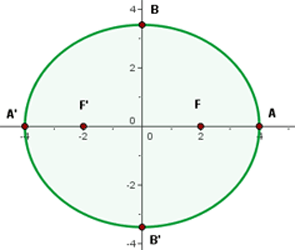
2 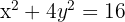

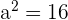
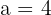
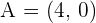
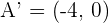
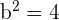

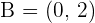

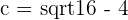
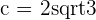


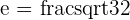

3 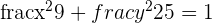
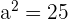


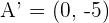


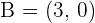
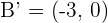



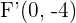

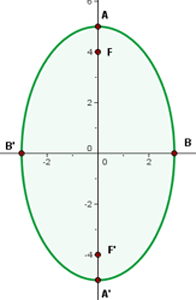
4 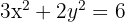
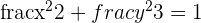

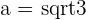
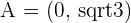



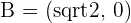

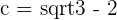

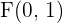
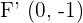
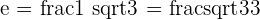

Solution of exercise 2
Calculate and plot the coordinates of the foci and vertices and determine the eccentricity of the following ellipses:
1 
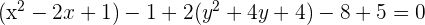


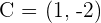







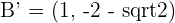
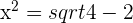
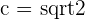
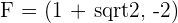

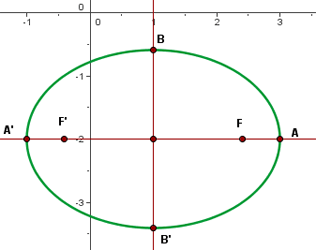
2 
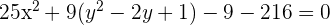
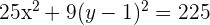
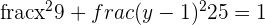
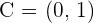
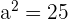

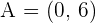
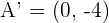



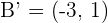





3 
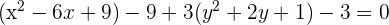


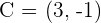
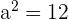

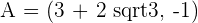

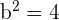



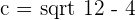
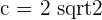

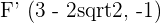

4 
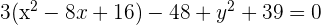
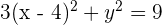
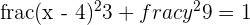
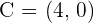
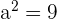


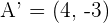
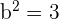


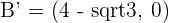
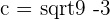
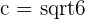
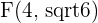
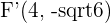
Solution of exercise 3
Determine the equations of the following ellipses using the information given:
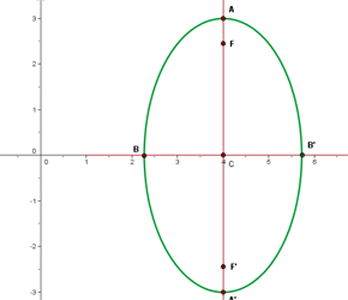
1 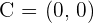 ,
,  ,
, 


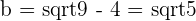
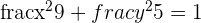
2 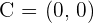 ,
, 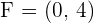 ,
, 



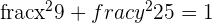
 ,
, 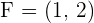
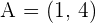


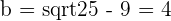
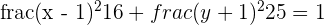 4
4  ,
, 




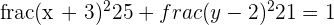
Solution of exercise 4
Determine the equation of the ellipse that is centered at (0, 0), passes through the point (2, 1) and whose minor axis is 4.
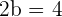



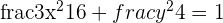
Solution of exercise 5
The focal length of an ellipse is 4 and the distance from a point on the ellipse is 2 and 6 units from each foci respectively. Calculate the equation of the ellipse if it is centered at (0, 0).


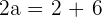
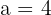
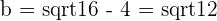


Solution of exercise 6
Determine the equation of the ellipse which is centered at (0, 0) and passes through the points:
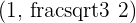 and
and 
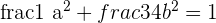
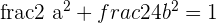



Solution of exercise 7
Find the coordinates of the midpoint of the chord in the line: x + 2y − 1 = 0 which intersects the ellipse: x² + 2y² = 3.
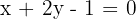




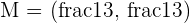

Solution of exercise 8
Determine the equation of the ellipse centered at (0, 0) whose focal length is  and the area of a rectangle in which the ellipse is inscribed within is 80 u².
and the area of a rectangle in which the ellipse is inscribed within is 80 u².

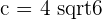
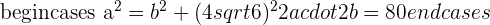

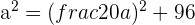
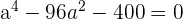



Solution of exercise 9
Find the equation of the locus of points P (x, y) whose sum of distances to the fixed points (4, 2) and (−2, 2) is equal to 8.
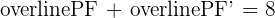


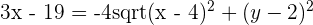
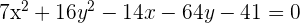
Solution of exercise 10
Determine the equation of the ellipse centered at (0, 0) knowing that one of its vertices is 8 units from a focus and 18 from the other.



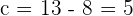
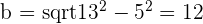

Solution of exercise 11
Determine the equation of the ellipse centered at (0, 0) knowing that it passes through the point (0, 4) and its eccentricity is 3/5.
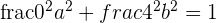
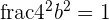

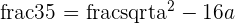
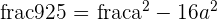

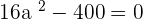
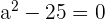















It is clear and understandable .
thankyouuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuu
This is very nice but please show how to find the 4p