¡Bienvenido a los ejercicios de ecuaciones de la recta en el plano! En esta serie de ejercicios, nos sumergiremos en el emocionante mundo de la geometría analítica y aprenderemos cómo representar y comprender las rectas en el plano cartesiano.
La ecuación de la recta es una herramienta fundamental para describir la relación lineal entre variables y entender cómo se comportan en función de los cambios en una o más dimensiones. A través de estos ejercicios, exploraremos diferentes formas de expresar la ecuación de una recta, como la forma continua, la forma punto-pendiente o incluso la forma general.
Distancia entre puntos y rectas
1Calcula la distancia del punto 
a la recta 
de ecuación 
Para una ecuación de la recta expresada en su forma ordinaria 
y un punto 
, es posible calcular su distancia a través de la siguiente fórmula:
En este caso, los coeficientes y las coordenadas del punto, quedan determinados de la siguiente manera
Haciendo una sustitución de estas variables en la fórmula anterior, obtenemos
Es decir, la distancia entre y 
es igual a
2Hallar la distancia entre 
y 
Dadas las rectas y 
, sucede uno y sólo uno de los escenarios siguientes: o éstas son paralelas o tienen algún punto en común.
De ser rectas paralelas, son ajenas o coinciden. Es decir, son ajenas o son la misma recta.Es por lo anterior, que antes de calcular la distancia entre dos rectas, es necesario realizar el cálculo de su pendiente para saber en qué caso nos encontramos.
De tener la misma pendiente serán rectas paralelas y en caso contrario se cruzarán en algún punto.
Para una ecuación de la recta expresada en su forma ordinaria
su pendiente está determinada por la expresión 
.
Entonces, particularmente y , tienen pendientes
y 
Como ambas rectas tienen la misma pendiente, podemos concluir que son paralelas; denotamos a esta relación como 
Dado que 
, debemos verificar si son la misma recta o son distintas. Para ello basta hallar un punto en que no pertenezca a . Con esta idea en mente, hagamos 
en la ecuación de para obtener 
; esto implica que 
es un punto en la recta pero no un punto en pues
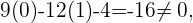
lo cual comprueba que este punto no satisface la ecuación que define a . Con ello podemos concluir que y son rectas distintas.
Ahora, buscamos un punto de cualquiera de ellas y calculamos la distancia de este punto a la recta restante. Nos valdremos de 
pues ya sabemos que 
.
Finalmente haciendo uso de la fórmula
obtenemos
3Una recta es paralela a la que tiene por ecuación 
, y dista 
unidades del origen. ¿Cuál es su ecuación?
Nombremos a la recta que estamos buscando como 
. Como sabemos, dos rectas son paralelas si los coeficientes de 
e 
respectivos son proporcionales, y como ha de suceder que 
y en particular los coeficientes iguales son proporcionales, la ecuación que describe a debe ser de la forma 
.
Por otro lado, recordemos que la distancia de un punto 
a una recta se puede encontrar a través de la fórmula
Si el punto resulta ser el origen, entonces la fórmula anterior se reduce a
Esto quiere decir que 
debe cumplir con
Observemos que realmente existe un par de rectas, que tienen distancia con el origen y que son paralelas entre sí, es por ello que
Y así las ecuaciones de este par de rectas están dadas por 
.
4Se tiene el cuadrilátero 
cuyos vértices son 
y 
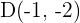. Calcular su área.
Comencemos notando que el área que buscamos es el resultado de multiplicar las magnitudes 
y 
. Procedamos entonces a calcular cada magnitud.
Al multiplicar los resultados anteriores se obtiene
Por lo tanto, el área del cuadrilátero es de 20.
Ángulos entre rectas
5Calcular el ángulo que forman las rectas y , sabiendo que sus vectores directores son: 
y 
Si 
y 
son un par de vectores no nulos, el ángulo formado entre ellos es el único número real 
que satisface
donde
y
Realizando los cálculos correspondientes tenemos que
Por tanto,
y así 
6Calcula el ángulo que forman las rectas 
y 
Para calcular el ángulo que forman dos rectas podemos usar la fórmula siguiente:
donde 
y 
son las pendientes de las rectas y respectivamente.
Una vez que la ecuación de la recta se escriba de la forma 
, el coeficiente que acompaña a , es decir 
, es la pendiente. Con esto en mente y representado a y como sigue
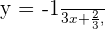
inferimos que 
y 
Luego, sustituyendo obtenemos
Por lo tanto 
.
7Hallar una recta paralela y otra perpendicular a 
, que pasen por el punto 
.
Recordemos que dos rectas serán paralelas si tienen la misma pendiente. Entonces, para encontrar una recta paralela a 
primero debemos conocer su pendiente.
Notemos que la definición de es equivalente a
y con esta expresión fácilmente podemos conocer la pendiente de dicha recta, pues es el coeficiente que acompaña a , o sea 
.
Llamando a la recta paralela a que pasa por el punto 
y a su pendiente, hemos encontrado que 
donde es la pendiente de .
Ahora con las coordenadas de 
podemos hacer uso de la ecuación punto-pendiente de la recta, que está descrita por 
.
Sustituyendo se sigue que
Con estos cálculos podemos concluir que 
, con 
.
Para encontrar una recta perpendicular a seguiremos el mismo razonamiento anterior, pero con una condición distinta en la pendiente; nombremos 
a la recta perpendicular que deseamos encontrar. En este caso su pendiente 
debe satisfacer la condición 
para asegurar perpendicularidad. Entonces 
, pues 
.
Invocando de nuevo la ecuación punto-pendiente de la recta y las coordenadas de , tenemos que
Y así queda definida por la ecuación 
, donde 
.
8Hallar la ecuación de la mediatriz del segmento de extremos 
y 
.
Dado un segmento, su mediatriz es el lugar geométrico de los puntos del plano que equidistan de los extremos. En términos matemáticos esto se traduce a los puntos 
que satisfacen la igualdad
para y 
extremos.Tengamos en cuenta que
y 
Para encontrar la ecuación deseada, procedemos a igualar estas ecuaciones y simplificar los términos.
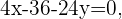
y multiplicando la ecuación por 
podemos simplificarla aún más, obteniendo la expresión
¿Y si pruebas con nuestras clases particulares matematicas?
9Hallar las ecuaciones de las bisectrices de los ángulos que determinan las rectas 
y 
.
Dadas dos rectas que se intersectan, la bisectriz del ángulo que forman es el lugar geométrico de los puntos en el plano que equidistan de éstas. Entonces buscamos la ecuación que describe a los puntos tales que
Por otro lado, la fórmula de la distancia de un punto 
a una recta 
está dada por la expresión
De la fórmula anterior se sigue que
y
Haciendo 
, obtenemos
Y multiplicando ésta última por 
se sigue que
De aquí, por el valor absoluto obtenemos dos ecuaciones:
y
donde cada una nos va a describir la ecuación de las respectivas bisectrices.
Para la primera ecuación obtenemos
Mientras que para la segunda,
10Calcular la ecuación de la recta perpendicular a 
que pasa por el punto 
.
Notemos que la pendiente de la recta es 
, pues al estar expresada en la forma 
, la pendiente es simplemente el coeficiente que acompaña a .
Si es la ecuación de la recta perpendicular a que pasa por 
Entonces su pendiente debe ser 
pues el producto de ambas pendientes debe dar como resultado -1, para obtener ortogonalidad.
Ahora con las coordenadas de 
podemos hacer uso de la ecuación punto-pendiente de la recta, que está descrita como 
Sustituyendo, se sigue que la ecuación buscada es
o equivalentemente
11Calcular las bisectrices de los ángulos determinados por la rectas:
Dadas dos rectas que se intersectan, la bisectriz del ángulo que forman es el lugar geométrico de los puntos en el plano que equidistan de éstas. Entonces buscamos la ecuación que describe a los puntos tales que .
Luego,
y
Haciendo , obtenemos
Y multiplicando ésta última por se sigue que
De aquí, por el valor absoluto obtenemos dos ecuaciones:
y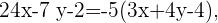 
donde cada una nos va a describir la ecuación de las respectivas bisectrices.
Para la primera ecuación obtenemos
Mientras que para la segunda,
¿Vives en la capital y buscas un profesor particular matematicas madrid? ¡No busques más!
12Hallar el ángulo que forman las rectas que tienen por ecuaciones:
a
b
aComo las ecuaciones de las rectas se encuentran en su forma paramétrica, podemos identificar a sus vectores directores como los coeficientes que acompañan a sus parámetros 
. Es decir 
es vector director de 
, y 
es vector director de 
.
De aquí, recurriendo a la fórmula de ángulo entre vectores
podemos calcular el ángulo que estamos buscando.
Sustituyendo las coordenadas de 
bNotemos que los vectores directores de estas rectas son 
y 
respectivamente.
El ángulo formado entre ellos está determinado por la expresión
13Hallar el ángulo que forman las rectas que tienen por ecuaciones:
a
b
aComo primer paso debemos encontrar los vectores directores de cada una de las rectas para después calcular en ángulo entre éstos. Esto nos dará el ángulo entre y .
Una recta descrita en su ecuación cartesiana , tiene como vector director 
. Entonces para y tenemos vectores directores 
y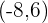 
.
El ángulo determinado entre estos dos vectores está dado por la fórmula:
Sustituyendo los vectores directores que hemos encontrado, tenemos
bEn este caso los vectores directores de las rectas 
y 
son 
y 
.
Observemos que
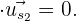
Esto significa que el ángulo entre y es de 90º, pues la condición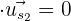 
es equivalente a que 
.
14Dadas las rectas 
y 
, determinar para que formen un ángulo de 
.
Sean 
y 
los vectores directores de de y respectivamente, buscamos de tal manera que
pues la fórmula anterior nos ayuda a encontrar el ángulo entre dos rectas.
Sustituyendo las coordenadas de lo vectores directores y 
, obtenemos
y elevando al cuadrado toda la ecuación
multiplicando por 
toda la ecuación
A través de la fórmula general para ecuaciones cuadráticas
podemos resolver la ecuación anterior.
Recordemos que 
es el coeficiente del término cuadrático, 
el coeficiente del término lineal y 
el término independiente. Para nuestro caso se encuentran determinados de la manera siguiente
Por lo tanto, siguiendo la fórmula general
Luego, obtenemos que los posibles valores para satisfacer la condición deseada son 
y 
15Una recta es perpendicular a la que tiene por ecuación 
y dista 
unidades del origen ¿Cuál es su ecuación?
Para una recta cualquiera 
, expresada en su forma canónica
tiene como coordenadas de su vector director 
.
Por otro lado, sabemos que dos rectas 
son perpendiculares si sus vectores directores 
lo son, o equivalentemente si
donde 
En nuestro caso, el vector director de es 
.
Si llamamos a la recta deseada, siguiendo la condición del párrafo anterior, se debe tener que el vector director de tiene por coordenadas 
, y así 
.
Por otro lado, recordemos que la distancia de un punto a una recta se puede encontrar a través de la fórmula
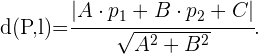
Si el punto resulta ser el origen, entonces la fórmula anterior se reduce a
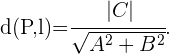
Esto quiere decir que debe cumplir con
Observemos que realmente existe un par de rectas, que tienen distancia con el origen y que son paralelas entre sí, es por ello que
y así las ecuaciones de este par de rectas están dadas por 
.
Ejercicios avanzados
16Dado el triángulo 
; calcular las ecuaciones de las alturas y determinar el ortocentro del triángulo.
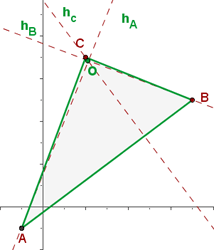
Como primer paso, calculemos las ecuaciones de las alturas del triángulo definido. Llamemos 
y 
a las ecuaciones de las rectas que pasan por los puntos 
y 
respectivamente.
Para 
tenemos que 
, eso quiere decir que la pendiente 
del segmento 
multiplicada por la pendiente 
de debe dar como resultado 
Al conocer las coordenadas de los puntos y podemos obtener su pendiente a tráves de la fórmula 
. Por tanto
y
Con las coordenadas de , 
y la forma punto pendiente, podemos deducir la ecuación de la recta para . Entonces 
es la ecuación que define .
Simplificando esta última se sigue que 
.
Siguiendo el mismo razonamiento, podemos encontrar las ecuaciones restantes.
Comenzamos por las pendientes.
Luego con la forma punto pendiente para 
y para 
Para encontrar las coordenadas del ortocentro es suficiente encontrar la intersección de cualesquiera dos alturas.
Resolviendo el sistema de ecuaciones lineales
encontramos que el ortocentro se encuentra situado en 
17Dado el triángulo 
; calcular las ecuaciones de las medianas y determinar el baricentro del triángulo.
Como primer paso, calculemos los puntos medios de los lados del triángulo definido. Llamemos 
a los puntos medios de 
, respectivamente
,
,
,
Calculemos las ecuaciones de las medianas del triángulo definido. Llamemos 
y 
a las ecuaciones de las medianas que pasan por los puntos y respectivamente.
Al conocer las coordenadas de los puntos 
y podemos obtener su pendiente a tráves de la fórmula . Por tanto
Con las coordenadas de , 
y la forma punto pendiente, podemos deducir la ecuación de la recta para 
. Entonces 
es la ecuación que define .
Simplificando esta última se sigue que 
.
Siguiendo el mismo razonamiento, podemos encontrar las ecuaciones restantes.
.
.
Para encontrar las coordenadas del baricentro es suficiente encontrar la intersección de cualesquiera dos medianas.
Resolviendo el sistema de ecuaciones lineales
encontramos que el baricentro se encuentra situado en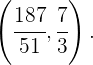 
18Dado el triángulo ; calcular las ecuaciones de las mediatrices y determinar el circuncentro del triángulo.
Como primer paso, calculemos los puntos medios de los lados del triángulo definido. Llamemos a los puntos medios de , respectivamente
,
,
,
Calculemos las ecuaciones de las mediatrices del triángulo definido. Llamemos 
y 
a las ecuaciones de las mediatrices que pasan por los puntos medios 
y respectivamente.
Al conocer las coordenadas de los puntos y podemos obtener la pendiente de los lados a tráves de la fórmula y sabiendo que la pendiente de su perpendicular es el recíproco negativo de la pendiente, se tiene
Con las coordenadas de 
, 
y la forma punto pendiente, podemos deducir la ecuación de la recta para 
. Entonces 
es la ecuación que define .
Simplificando esta última se sigue que 
.
Siguiendo el mismo razonamiento, podemos encontrar las ecuaciones restantes.
.
.
Para encontrar las coordenadas del circuncentro es suficiente encontrar la intersección de cualesquiera dos mediatrices.
Resolviendo el sistema de ecuaciones lineales
encontramos que el baricentro se encuentra situado en 
19Una recta de ecuación 
es mediatriz de un segmento 
cuyo extremo tiene por coordenadas 
. Hallar las coordenadas del otro extremo.
Llamemos a la ecuación que describe la recta sobre la que descansan el segmento y el punto .
Notemos que al ser mediatriz del segmento cumple con satisfacer 
, lo cual implica que 
donde y son las pendientes respectivas de las rectas y .
Del razonamiento anterior obtenemos que 
, pues expresando a en su forma equivalente 
, sabemos que 
.
Con la ecuación punto pendiente, podemos encontrar la ecuación que describe a la recta que pasa por el punto y tiene pendiente . Basta con reducir la expresión 
y obtener 
.
Ahora observemos que 
, el punto de intersección entre y , debe satisfacer ambas ecuaciones, la que describe a y a . Es por ello que para encontrar las coordenadas de , basta con resolver el sistema de ecuaciones
Resolviendo el sistema, obtenemos que las coordenadas del punto son 
. Además, es punto medio del segmento , lo que matemáticamente significa que
donde 
son las coordenadas de respectivamente.
Igualando coordenada a coordenada, se tiene que
Y sustituyendo los valores que ya conocemos de y se sigue que
y luego
Por lo tanto el extremo tiene como coordenadas 
.
20Halla el punto simétrico 
, del punto 
, respecto de la recta 
Llamemos a la ecuación que describe la recta sobre la que descansan el segmento 
y el punto . Dadas nuestras hipótesis, se debe satisfacer que , esto implica que 
, donde y son las pendientes respectivas de las rectas y .
Por otro lado, la ecuación de en su forma explícita es 
, y de esta manera la pendiente de es simplemente el coeficiente que acompaña a equis, es decir 
. Con esto último podemos concluir que 
.
Con la ecuación punto pendiente, podemos encontrar la ecuación que describe a la recta que pasa por el punto y tiene pendiente . Basta con reducir la expresión
y obtener
.
Ahora observemos que , el punto de intersección entre y , debe satisfacer ambas ecuaciones: la que describe a y a . Es por ello que para encontrar las coordenadas de , basta con resolver el sistema de ecuaciones
Resolviendo el sistema, obtenemos que las coordenadas del punto son 
. Además, es punto medio del segmento , y en términos matemáticos es equivalente a
donde 
son las coordenadas de 
respectivamente.
Igualando coordenada a coordenada, se tiene que
Y sustituyendo los valores que ya conocemos de y se sigue que
y luego
Por tanto, el punto simétrico tiene como coordenadas 
.
Más ejercicios y problemas de la ecuación de la recta
¿Te ha gustado este artículo? ¡Califícalo!
Cargando...
Apuntes es una plataforma dirigida al estudio y la práctica de las matemáticas a través de la teoría y ejercicios interactivos que ponemos a vuestra disposición. Esta información está disponible para todo aquel/aquella que quiera profundizar en el aprendizaje de esta ciencia. Será un placer ayudaros en caso de que tengáis dudas frente algún problema, sin embargo, no realizamos un ejercicio que nos presentéis de 0 sin que hayáis si quiera intentado resolverlo. Ánimo, todo esfuerzo tiene su recompensa.
encuentre una forma general de una ecuación de la recta q pasa por el punto A q satisfaga la condicion dada A (5, – 2)
a) paralelo al eje y
b) perpendicular al eje y
¿Cuál es el lugar geométrico descrito por la trayectoria de un avión que se mantiene sobre volando la ciudad de San José a una distancia constante de 5 km de la Torre de Juan Santamaría
Graficar y calcular la distancia y punto Medio de los siguientes P(1,1),Q (3,3)
Hallar la distancia y la pendiente de A(07)
B(2,1)
F(×)=5-2×
A= (7,7)
B= (-9,-6)
Ecuación explícita de la recta
una recta pasa por el punto (0,-5) formando con una x un ángulo de x=90° Hallar la ecuación de la recta
1. Hallar las ecuaciones paramétricas de la recta que pasa por A(3,-1,0) y su vector director sea
perpendicular a los vectores: w = y u =