Elige la opción correcta en cada caso:
1Calcula una recta perpendicular a la recta 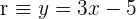 que pase por el punto
que pase por el punto 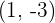
1La pendiente de la recta que nos dan es 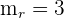 . Como tenemos que hallar una recta perpendicular a ésta, la pendiente de la nueva recta
. Como tenemos que hallar una recta perpendicular a ésta, la pendiente de la nueva recta  es
es
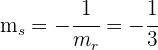 .
.
2Como tenemos la pendiente de la recta que queremos calcular y un punto por el que pasa, podemos utilizar la ecuación punto-pendiente.
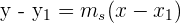
3Sustituimos los valores conocidos
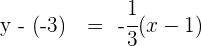
4Obtenemos la recta  perperdicular a
perperdicular a 

2Calcula una recta perpendicular a la recta  que pase por el punto
que pase por el punto 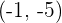
1La pendiente de la recta que nos dan es 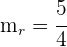 . Como tenemos que hallar una recta perpendicular a ésta, la pendiente de la nueva recta
. Como tenemos que hallar una recta perpendicular a ésta, la pendiente de la nueva recta  es
es
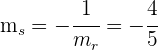 .
.
2Como tenemos la pendiente de la recta que queremos calcular y un punto por el que pasa, podemos utilizar la ecuación punto-pendiente.
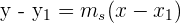
3Sustituimos los valores conocidos
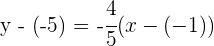
4Obtenemos la recta  perperdicular a
perperdicular a 
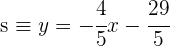
3Calcula una recta perpendicular a 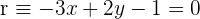 , que pasen por el punto
, que pasen por el punto 
1La pendiente de la recta que nos dan es 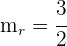 . Como tenemos que hallar una recta perpendicular a ésta, la pendiente de la nueva recta
. Como tenemos que hallar una recta perpendicular a ésta, la pendiente de la nueva recta  es
es
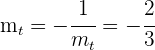 .
.
2Como tenemos la pendiente de la recta que queremos calcular y un punto por el que pasa, podemos utilizar la ecuación punto-pendiente
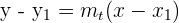
3Sustituimos los valores conocidos
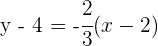
4Obtenemos la recta  perperdicular a
perperdicular a 
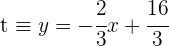
4La recta 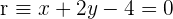 y la recta
y la recta  , perpendicular a
, perpendicular a  y que pasa por el punto
y que pasa por el punto 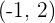 , se cortan en el punto de coordenadas:
, se cortan en el punto de coordenadas:
1La pendiente de la recta que nos dan es  . Como tenemos que hallar una recta perpendicular a ésta, la pendiente de la nueva recta
. Como tenemos que hallar una recta perpendicular a ésta, la pendiente de la nueva recta  es
es
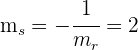 .
.
2Como tenemos la pendiente de la recta que queremos calcular y un punto por el que pasa, podemos utilizar la ecuación punto-pendiente.
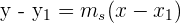
3Sustituimos los valores conocidos
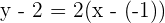
4Obtenemos la recta  perperdicular a
perperdicular a 
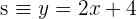
5Obtenemos Resolvemos el sistema de ecuaciones de las rectas  y
y  , para esto igualamos las variables
, para esto igualamos las variables 
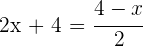
Despejando para  se obtiene
se obtiene 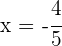
Sustituyendo en la recta  , se obtiene
, se obtiene 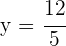
Así, el punto de intersección es 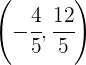
5Comprueba si las rectas  y
y 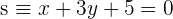 son perpendiculares
son perpendiculares
1La pendiente de la recta  es
es
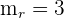 .
.
2La pendiente de la recta  es
es
 .
.
3Dos rectas son perpendiculares si el producto de sus pendientes es igual a 
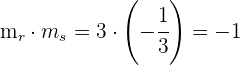 .
.
Luego las dos rectas son perpendiculares.
6Comprueba si la recta  que pasa por los puntos
que pasa por los puntos  y
y  , y la recta
, y la recta  que pasa por los puntos
que pasa por los puntos 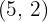 y
y 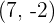 son perpendiculares entre si
son perpendiculares entre si
1La pendiente de la recta  es
es
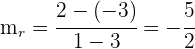 .
.
2La pendiente de la recta  es
es
 .
.
3Dos rectas son perpendiculares si el producto de sus pendientes es igual a 
 .
.
Luego las dos rectas no son perpendiculares.
7La recta perpendicular a la recta 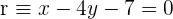 que pasa por el punto
que pasa por el punto 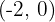 y la recta paralela a la recta
y la recta paralela a la recta 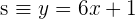 que pasa por el punto
que pasa por el punto  se cortan en el punto de coordenadas:
se cortan en el punto de coordenadas:
1La pendiente de la recta que nos dan es 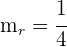 . Como tenemos que hallar una recta perpendicular a ésta, la pendiente de la nueva recta
. Como tenemos que hallar una recta perpendicular a ésta, la pendiente de la nueva recta  es
es
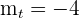 .
.
2Como tenemos la pendiente de la recta que queremos calcular y un punto por el que pasa, podemos utilizar la ecuación punto-pendiente.
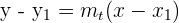
3Sustituimos los valores conocidos

4Obtenemos la recta  perperdicular a
perperdicular a 

5La pendiente de la recta  es
es 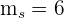 , por lo que la pendiente de la recta
, por lo que la pendiente de la recta  paralela a
paralela a  es
es 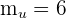
7Como tenemos la pendiente de la recta que queremos calcular y un punto por el que pasa, podemos utilizar la ecuación punto-pendiente.
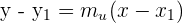
8Sustituimos los valores conocidos

9Obtenemos la recta  paralela a
paralela a 
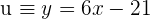
10Resolvemos el sistema de ecuaciones de las rectas  y
y  , para esto igualamos las variables
, para esto igualamos las variables 
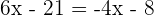
Despejando para  se obtiene
se obtiene 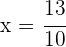
Sustituyendo en la recta  , se obtiene
, se obtiene 
Así, el punto de intersección es 
8La recta perpendicular a la recta  que pasa por el punto
que pasa por el punto  , es también:
, es también:
1La pendiente de la recta que nos dan es 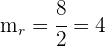 . Como tenemos que hallar una recta perpendicular a ésta, la pendiente de la
. Como tenemos que hallar una recta perpendicular a ésta, la pendiente de la  perpendicular a
perpendicular a  y que para por
y que para por  es
es
 .
.
2Calculamos la pendiente de la recta que pasa por los puntos  y
y 
 .
.
Luego la pendiente de cualquier recta paralela a  es
es 
3Calculamos la pendiente de la recta que pasa por los puntos 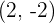 y
y 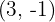
 .
.
Luego la pendiente de cualquier recta perpendicular a  es
es 
4Calculamos la pendiente de la recta que pasa por los puntos  y
y 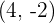
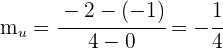 .
.
Luego la pendiente de cualquier recta paralela a  es
es 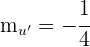
5Se cumple que  , por lo que la recta
, por lo que la recta  es paralela a la recta
es paralela a la recta 
Contesta a las siguientes cuestiones:
9Calcula  para que las rectas
para que las rectas 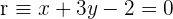 y
y 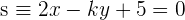 sean perpendiculares.
sean perpendiculares.
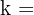
1La pendiente de las rectas que nos dan son 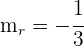 y
y  .
.
2Dos rectas son perpendiculares si el producto de sus pendiente es  .
.
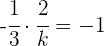 .
.
3Despejando  se obtiene
se obtiene  .
.
10Calcula  para que las rectas
para que las rectas 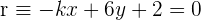 y
y  sean perpendiculares.
sean perpendiculares.
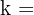
1Las pendientes de las rectas que nos dan son 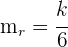 y
y  .
.
2Dos rectas son perpendiculares si el producto de sus pendiente es  .
.
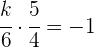 .
.
3Despejando  se obtiene
se obtiene 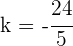 .
.
11Calcula  y
y  para que la recta
para que la recta 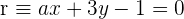 que pasa por el punto
que pasa por el punto 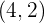 y la recta
y la recta  sean perpendiculares
sean perpendiculares
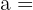 ,
, 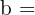
1Como el punto 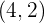 para por la recta
para por la recta  , entonces podemos sustituir y obtener
, entonces podemos sustituir y obtener 
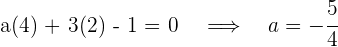 .
.
2Las pendientes de las rectas que nos dan son 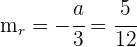 y
y 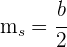 .
.
2Dos rectas son perpendiculares si el producto de sus pendiente es  .
.
 .
.
3Despejando  se obtiene
se obtiene  .
.
12Calcula  y
y  para que la recta
para que la recta 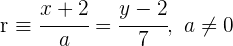 que pasa por el punto
que pasa por el punto 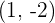 y la recta
y la recta 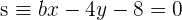 sean perpendiculares
sean perpendiculares
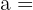 ,
, 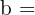
1Como el punto 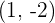 para por la recta
para por la recta  , entonces podemos sustituir y obtener
, entonces podemos sustituir y obtener 
 .
.
2Las pendientes de las rectas que nos dan son 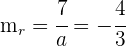 y
y 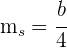 .
.
2Dos rectas son perpendiculares si el producto de sus pendiente es  .
.
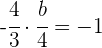 .
.
3Despejando  se obtiene
se obtiene  .
.
Si tienes dudas puedes consultar la teoría



Apuntes es una plataforma dirigida al estudio y la práctica de las matemáticas a través de la teoría y ejercicios interactivos que ponemos a vuestra disposición. Esta información está disponible para todo aquel/aquella que quiera profundizar en el aprendizaje de esta ciencia. Será un placer ayudaros en caso de que tengáis dudas frente algún problema, sin embargo, no realizamos un ejercicio que nos presentéis de 0 sin que hayáis si quiera intentado resolverlo. Ánimo, todo esfuerzo tiene su recompensa.
encuentre una forma general de una ecuación de la recta q pasa por el punto A q satisfaga la condicion dada A (5, – 2)
a) paralelo al eje y
b) perpendicular al eje y
¿Cuál es el lugar geométrico descrito por la trayectoria de un avión que se mantiene sobre volando la ciudad de San José a una distancia constante de 5 km de la Torre de Juan Santamaría
Graficar y calcular la distancia y punto Medio de los siguientes P(1,1),Q (3,3)
Hallar la distancia y la pendiente de A(07)
B(2,1)
F(×)=5-2×
A= (7,7)
B= (-9,-6)
Ecuación explícita de la recta
una recta pasa por el punto (0,-5) formando con una x un ángulo de x=90° Hallar la ecuación de la recta
1. Hallar las ecuaciones paramétricas de la recta que pasa por A(3,-1,0) y su vector director sea
perpendicular a los vectores: w = y u =