Temas

¿Cómo saber si una función es creciente o decreciente?
Una función  es estrictamente creciente en el intervalo
es estrictamente creciente en el intervalo 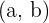 si
si 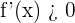 para todos los valores de
para todos los valores de  en
en 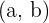 .
.
Una función  es estrictamente decreciente en el intervalo
es estrictamente decreciente en el intervalo 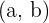 si
si  para todos los valores de
para todos los valores de  en
en 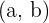 .
.
Intervalos de crecimiento y decrecimiento
Para encontrar los intervalos 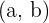 donde la función
donde la función  es creciente o decreciente, se realiza lo siguiente:
es creciente o decreciente, se realiza lo siguiente:
1 Derivar la función.
2 Obtener las raíces de la derivada primera, esto es, encontrar los valores  que cumplen
que cumplen 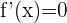 .
.
3 Formar intervalos abiertos con los ceros (raíces) de la derivada primera y los puntos de discontinuidad (si los hubiese)
4 Elegir un valor de cada intervalo y hallar el signo que tiene en la derivada primera.
5 Elegir los intervalos de crecimiento y decrecimiento de acuerdo al signo obtenido en el paso anterior.
Ejercicios propuestos
1Hallar los intervalos de crecimiento y decrecimiento de 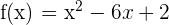
1 Derivamos la función
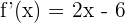
2 Calculamos las raíces de la derivada primera, para esto igualamos la derivada a cero y resolvemos para 
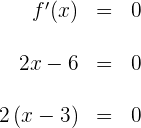
igualando los factores a cero, se tiene que las raíces son  .
.
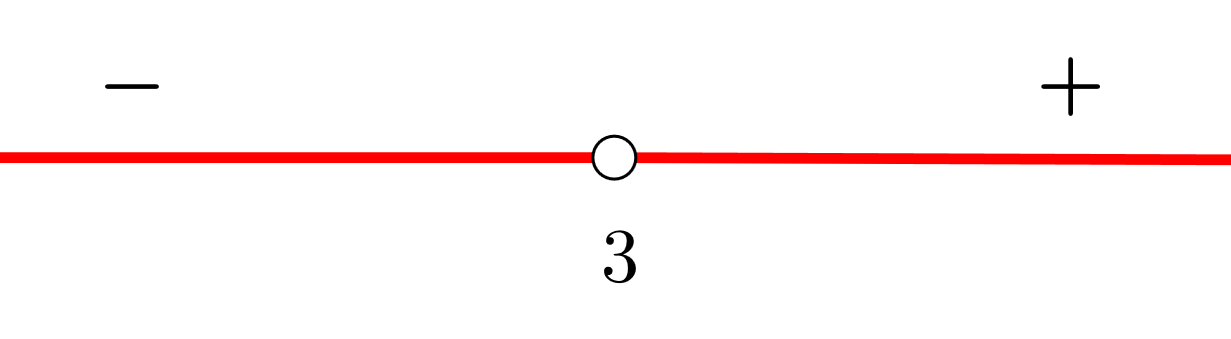
3 Formamos intervalos abiertos con los ceros de la derivada primera, en este caso no existen puntos de discontinuidad. Nos apoyamos con la representación de los puntos en la recta real
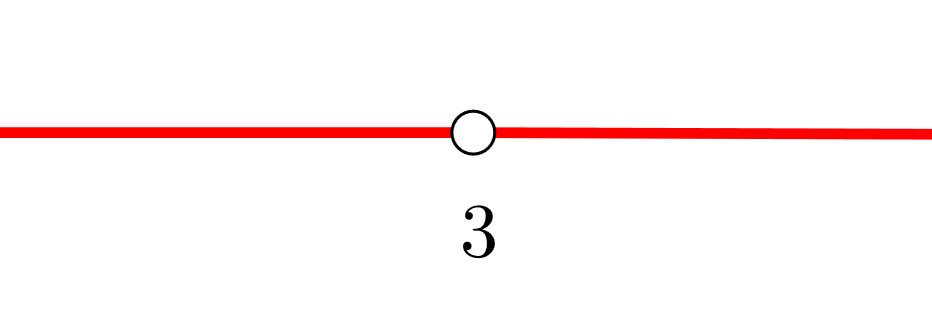
Los intervalos que obtenemos son  y
y 
4 Tomamos un valor de cada intervalo (puedes tomar cualquier valor en el intervalo) y hallamos el signo que tiene en la derivada primera
Para el intervalo  tomamos
tomamos  y sustituimos en la derivada y obtenemos
y sustituimos en la derivada y obtenemos

Para el intervalo  tomamos
tomamos 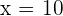 , sustituimos en la derivada y obtenemos
, sustituimos en la derivada y obtenemos

5 Escribimos los intervalos de crecimiento y decrecimiento
De crecimiento: 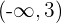
De decrecimiento: 
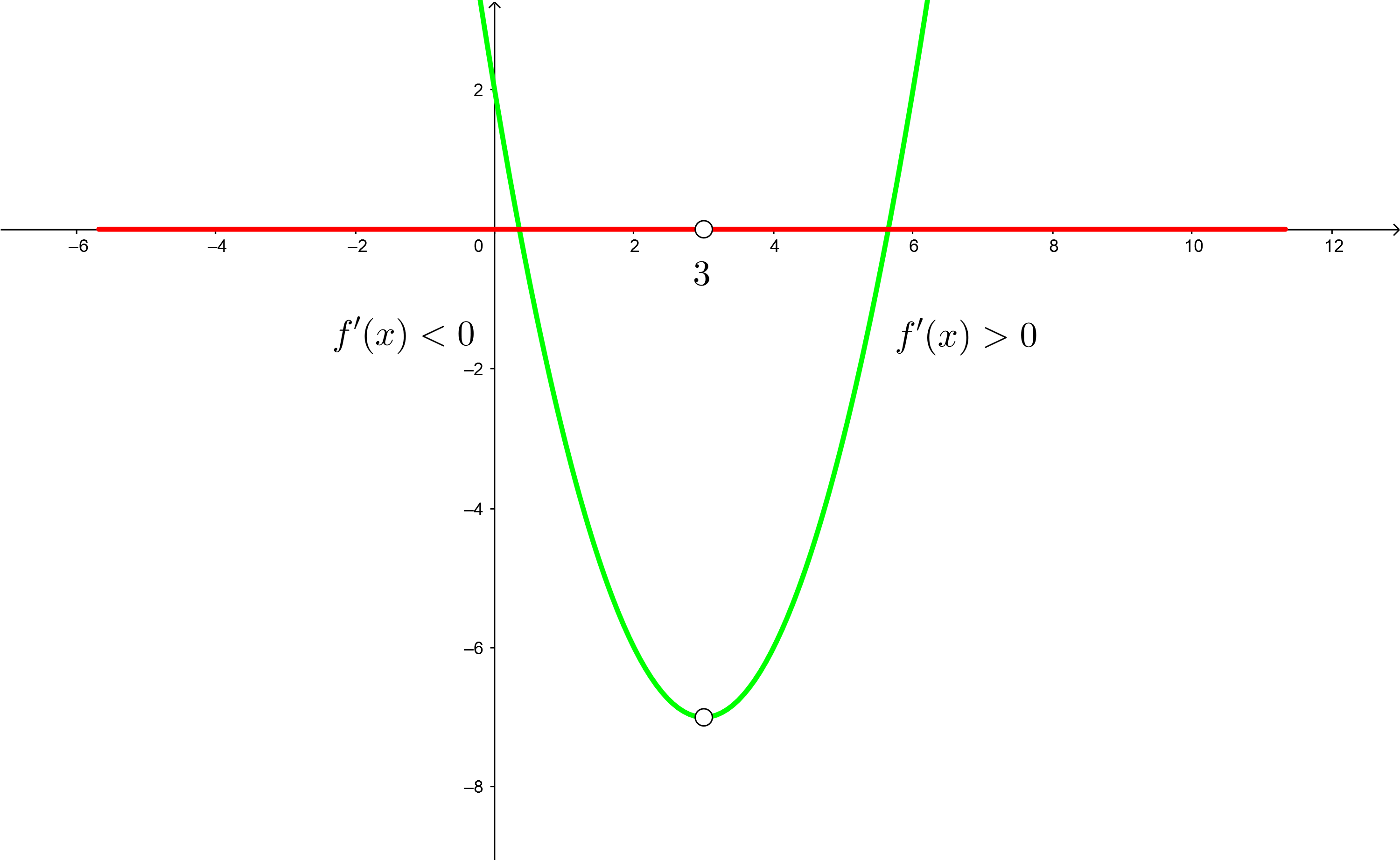
2Hallar los intervalos de crecimiento y decrecimiento de 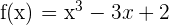
1 Derivamos la función
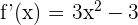
2 Calculamos las raíces de la derivada primera, para esto igualamos la derivada a cero y resolvemos para 
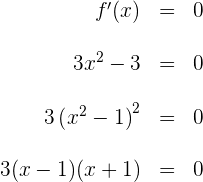
igualando los factores a cero, se tiene que las raíces son 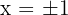 .
.
3 Formamos intervalos abiertos con los ceros de la derivada primera, en este caso no existen puntos de discontinuidad. Nos apoyamos con la representación de los puntos en la recta real

Los intervalos que obtenemos son 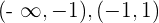 y
y 
4 Tomamos un valor de cada intervalo (puedes tomar cualquier valor en el intervalo) y hallamos el signo que tiene en la derivada primera
Para el intervalo 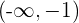 tomamos
tomamos  , sustituimos en la derivada y obtenemos
, sustituimos en la derivada y obtenemos
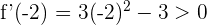
Para el intervalo  tomamos
tomamos  , sustituimos en la derivada y obtenemos
, sustituimos en la derivada y obtenemos

Para el intervalo  tomamos
tomamos  , sustituimos en la derivada y obtenemos
, sustituimos en la derivada y obtenemos
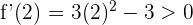

5 Escribimos los intervalos de crecimiento y decrecimiento
De crecimiento: 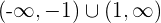
De decrecimiento: 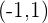
3Hallar los intervalos de crecimiento y decrecimiento de 
1 Derivamos la función
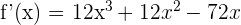
2 Calculamos las raíces de la derivada primera, para esto igualamos la derivada a cero y resolvemos para 
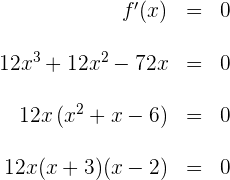
igualando los factores a cero, se tiene que las raíces son 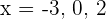 .
.
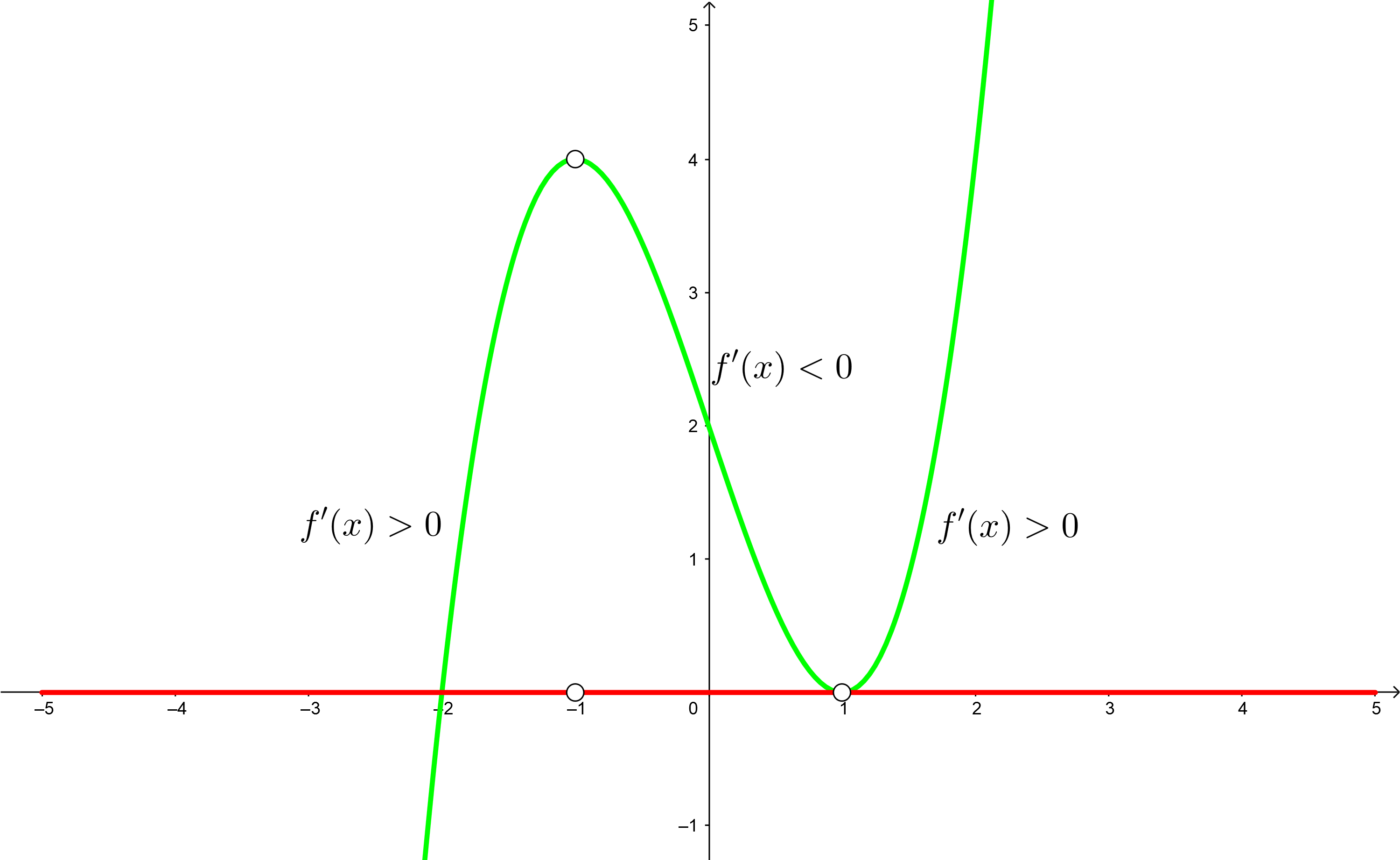
3 Formamos intervalos abiertos con los ceros de la derivada primera, en este caso no existen puntos de discontinuidad. Nos apoyamos con la representación de los puntos en la recta real

Los intervalos que obtenemos son 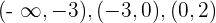 y
y 
4 Tomamos un valor de cada intervalo (puedes tomar cualquier valor en el intervalo) y hallamos el signo que tiene en la derivada primera
Para el intervalo  tomamos
tomamos 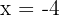 , sustituimos en la derivada y obtenemos
, sustituimos en la derivada y obtenemos

Para el intervalo  tomamos
tomamos  , sustituimos en la derivada y obtenemos
, sustituimos en la derivada y obtenemos

Para el intervalo  tomamos
tomamos  , sustituimos en la derivada y obtenemos
, sustituimos en la derivada y obtenemos

Para el intervalo 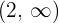 tomamos
tomamos  , sustituimos en la derivada y obtenemos
, sustituimos en la derivada y obtenemos

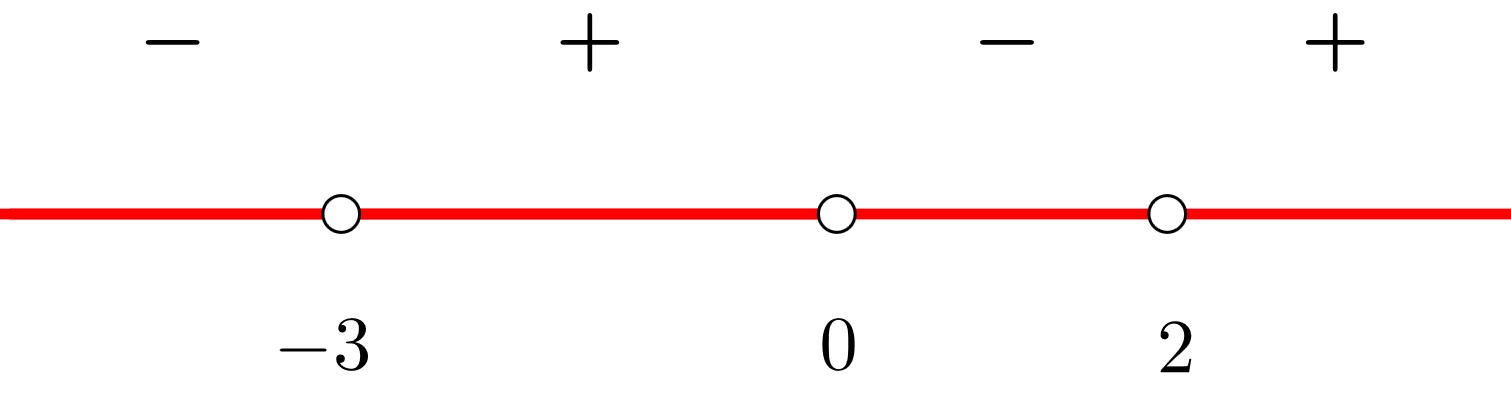
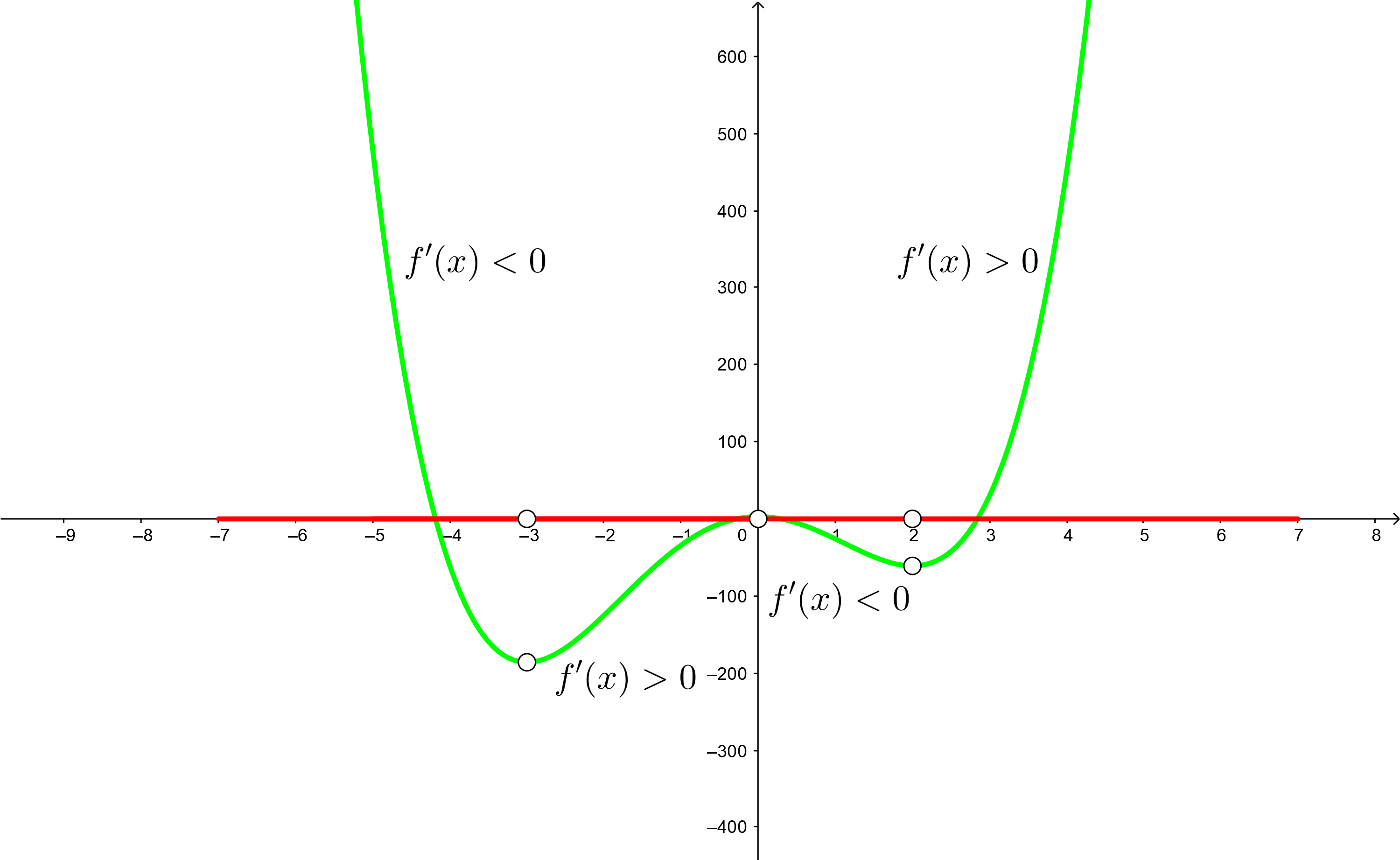
5 Escribimos los intervalos de crecimiento y decrecimiento
De decrecimiento: 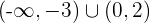
De crecimiento: 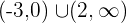
4Hallar los intervalos donde es creciente y decreciente la función 
1 Derivamos la función

2 Calculamos las raíces de la derivada primera (si existen), para esto igualamos la derivada a cero y resolvemos para 
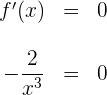
no existen valores de  en los números reales que satisfagan la ecuación anterior, por tanto la derivada primera no posee raíces. Observamos que la función y su derivada poseen una discontinuidad en
en los números reales que satisfagan la ecuación anterior, por tanto la derivada primera no posee raíces. Observamos que la función y su derivada poseen una discontinuidad en  .
.
3 Formamos intervalos abiertos con la discontinuidad, en este caso no existen ceros de la derivada. Nos apoyamos con la representación de los puntos en la recta real
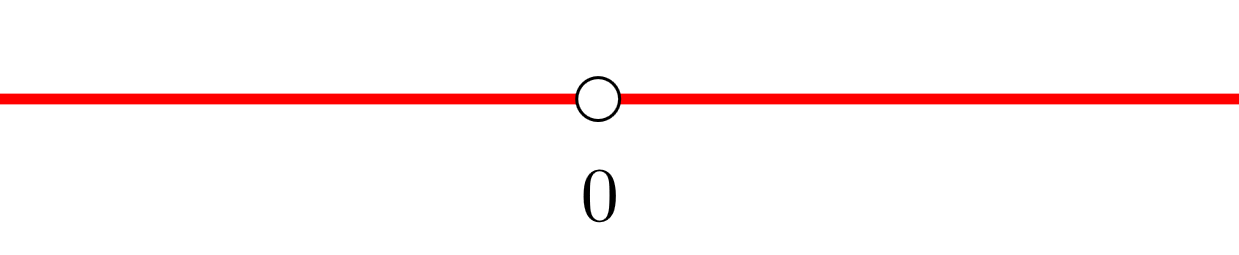
Los intervalos que obtenemos son 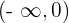 y
y 
4 Tomamos un valor de cada intervalo (puedes tomar cualquier valor en el intervalo) y hallamos el signo que tiene en la derivada primera
Para el intervalo  tomamos
tomamos  , sustituimos en la derivada y obtenemos
, sustituimos en la derivada y obtenemos
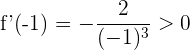
Para el intervalo 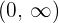 tomamos
tomamos  , sustituimos en la derivada y obtenemos
, sustituimos en la derivada y obtenemos


5 Escribimos los intervalos de crecimiento y decrecimiento
De crecimiento: 
De decrecimiento: 

5Hallar los intervalos donde es creciente y decreciente la función 
1 Derivamos la función
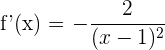
2 Calculamos las raíces de la derivada primera (si existen), para esto igualamos la derivada a cero y resolvemos para 

no existen valores de  en los números reales que satisfagan la ecuación anterior, por tanto la derivada primera no posee raíces. Observamos que la función y su derivada poseen una discontinuidad en
en los números reales que satisfagan la ecuación anterior, por tanto la derivada primera no posee raíces. Observamos que la función y su derivada poseen una discontinuidad en  .
.
3 Formamos intervalos abiertos con la discontinuidad, en este caso no existen ceros de la derivada. Nos apoyamos con la representación de los puntos en la recta real
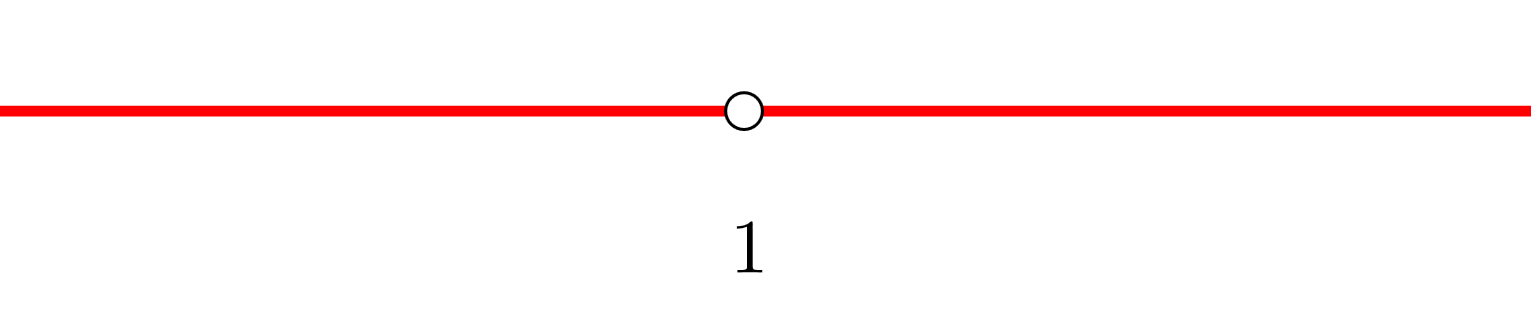
Los intervalos que obtenemos son 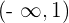 y
y 
4 Tomamos un valor de cada intervalo (puedes tomar cualquier valor en el intervalo) y hallamos el signo que tiene en la derivada primera
Para el intervalo  tomamos
tomamos  , sustituimos en la derivada y obtenemos
, sustituimos en la derivada y obtenemos

Para el intervalo  tomamos
tomamos  , sustituimos en la derivada y obtenemos
, sustituimos en la derivada y obtenemos

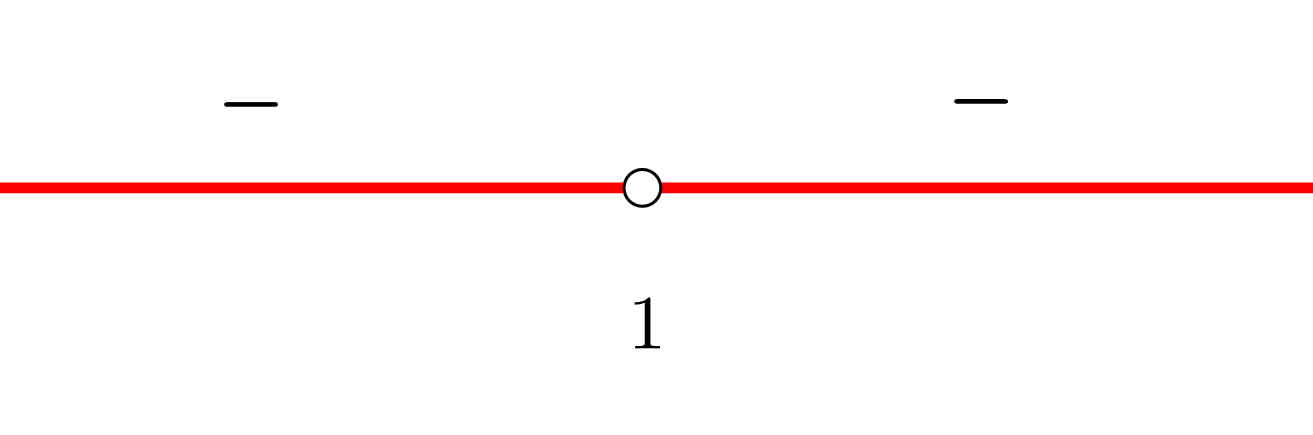
5 Como al evaluar en la derivada el resultado siempre fue negativo, entonces solamente se tienen intervalos de decrecimiento
De decrecimiento: 

6Hallar los intervalos donde es creciente y decreciente la función 
1 Derivamos la función
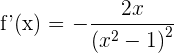
2 Calculamos las raíces de la derivada primera (si existen), para esto igualamos la derivada a cero y resolvemos para 

 es el único valor que satisface la ecuación anterior. Observamos que la función y su derivada poseen discontinuidades en
es el único valor que satisface la ecuación anterior. Observamos que la función y su derivada poseen discontinuidades en 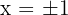 .
.
3 Formamos intervalos abiertos con las discontinuidades y el cero de la derivada. Nos apoyamos con la representación de los puntos en la recta real
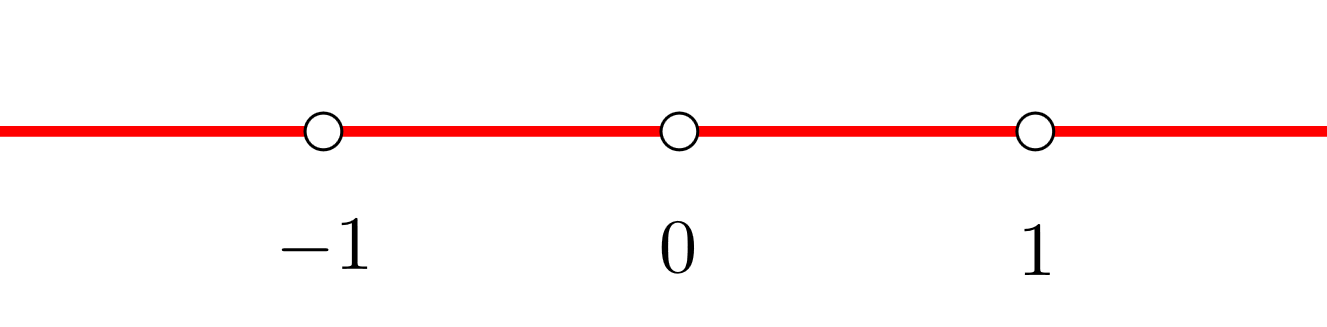
Los intervalos que obtenemos son  y
y 
4 Tomamos un valor de cada intervalo (puedes tomar cualquier valor en el intervalo) y hallamos el signo que tiene en la derivada primera
Para el intervalo 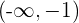 tomamos
tomamos  , sustituimos en la derivada y obtenemos
, sustituimos en la derivada y obtenemos

Para el intervalo  tomamos
tomamos 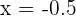 , sustituimos en la derivada y obtenemos
, sustituimos en la derivada y obtenemos

Para el intervalo  tomamos
tomamos 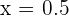 , sustituimos en la derivada y obtenemos
, sustituimos en la derivada y obtenemos

Para el intervalo  tomamos
tomamos  , sustituimos en la derivada y obtenemos
, sustituimos en la derivada y obtenemos

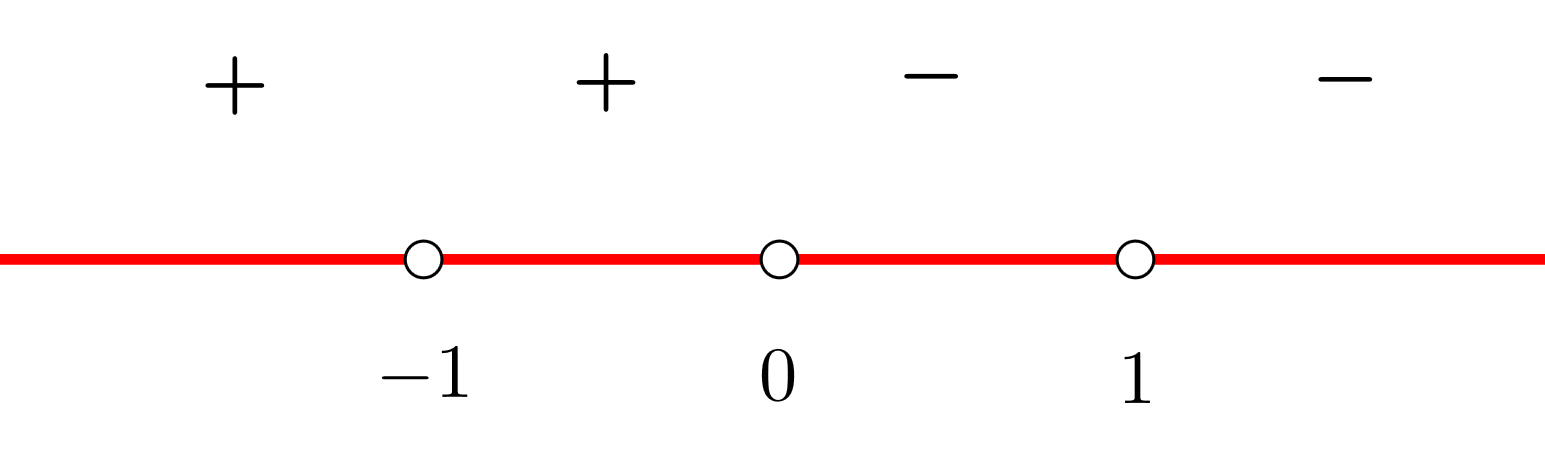
5 Escribimos los intervalos de crecimiento y decrecimiento
De crecimiento: 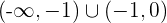
De decrecimiento: 

Para consultar más ejercicios pulsa aqui.













Apuntes es una plataforma dirigida al estudio y la práctica de las matemáticas a través de la teoría y ejercicios interactivos que ponemos a vuestra disposición. Esta información está disponible para todo aquel/aquella que quiera profundizar en el aprendizaje de esta ciencia. Será un placer ayudaros en caso de que tengáis dudas frente algún problema, sin embargo, no realizamos un ejercicio que nos presentéis de 0 sin que hayáis si quiera intentado resolverlo. Ánimo, todo esfuerzo tiene su recompensa.
Y=x³ x=1 ∆x=0.02
Dy= 3x^2 • dx
dy= 3(1)^2 • 0.02
dy= 0.06
Considera la curva de ecuación y=-X³ + 26X y halla sus rectas tangentes que sean paralelas a la recta y= -X.
f(x)= 4x-2
hola me pode hayudar con este problema Realizar la derivada por definición de f(x) = x³+1 en x = 0.
De acuerdo con la definición de derivada de una función
f´(x)=〖lim〗┬(h→0)〖(f(x+h)-f(x))/h〗
Calcular la derivada de las siguientes funciones siguiendo el proceso del límite:
f(x)=1/2 x^3+2x+3
4(x+h)-4x/h =4x+4h-4x/h= 4h/h= 4