Temas

Halla los puntos
1 Dada la parábola  , hallar los puntos en los que la recta tangente es paralela a la bisectriz del primer cuadrante. Encuentra la ecuación de la recta tangente y normal en dichos puntos.
, hallar los puntos en los que la recta tangente es paralela a la bisectriz del primer cuadrante. Encuentra la ecuación de la recta tangente y normal en dichos puntos.
1 Encontrar los puntos
La bisectriz del primer cuadrante tiene de ecuación  , por tanto
, por tanto 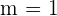 .
.
Derivamos la ecuación de la parábola, pues sabemos que la derivada nos indica la pendiente
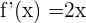
e igualamos a  y despejamos para calcular el valor de x en el que ocurre esto
y despejamos para calcular el valor de x en el que ocurre esto

Evaluamos la función original en este punto 
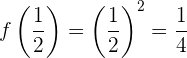
Entonces
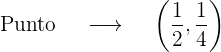
2 Recta tangente


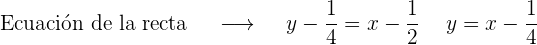
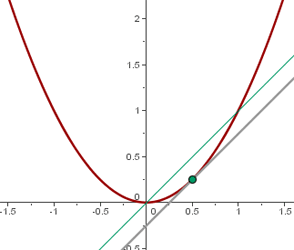
3 Recta normal

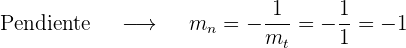
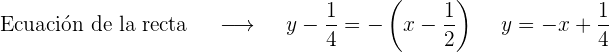
2 Dada la curva de ecuación  , halla las coordenadas de los puntos de dicha curva en los que la tangente forma con el eje
, halla las coordenadas de los puntos de dicha curva en los que la tangente forma con el eje  un ángulo de
un ángulo de 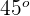 .
.
Lo primero que debemos saber es que la pendiente de una recta es igual a la tangente del ángulo que forma con el eje 
Es decir 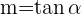
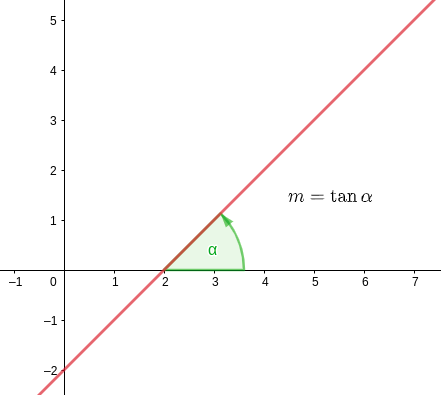
La derivada de  nos indica la pendiente de la recta tangente
nos indica la pendiente de la recta tangente
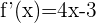
Como quiero que la recta tangente forme 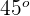 con el eje
con el eje  , estoy pidiendo que la pendiente tenga el valor de
, estoy pidiendo que la pendiente tenga el valor de 
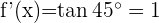
Entonces,
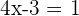
Despejamos
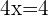
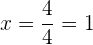
Al obtener el valor de x hemos obtenido la abscisa. Para obtener el valor de la ordenada, evaluamos el punto  en la función original
en la función original

Finalmente

3 Calcular los puntos en que la tangente a la curva 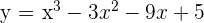 es paralela al eje
es paralela al eje  .
.
Las rectas paralelas tienen la misma pendiente. El eje  tiene pendiente cero.Entonces quiero que la tangente a la curva tenga pendiente cero. Así que quiero que
tiene pendiente cero.Entonces quiero que la tangente a la curva tenga pendiente cero. Así que quiero que
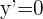
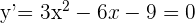
Simplificando obtenemos la ecuación

Resolvemos, y evaluamos las soluciones en la función 


Finalmente los puntos donde la tangente a la curva es paralela al eje  son:
son:


4 Se ha trazado una recta tangente a la curva 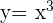 , cuya pendiente es
, cuya pendiente es  y pasa por el punto
y pasa por el punto  . Hallar el punto de tangencia.
. Hallar el punto de tangencia.
La derivada nos da la pendiente de la recta tangente a la curva
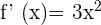
El problema dice que esta pendiente es  , entonces
, entonces
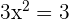
Resolvemos

Obtenemos la ecuación de la recta tangente en estos puntos
1 Abscisa x=1
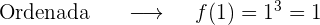

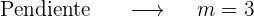
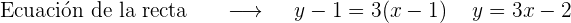
2 Abscisa x=-1
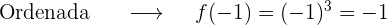
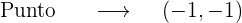
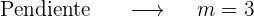

Pero el punto  sólo pertenece a la recta
sólo pertenece a la recta  .
.
Por tanto el punto de tangencia será 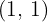 .
.
5 Buscar los puntos de la curva  , para los cuales la tangente forma un ángulo de
, para los cuales la tangente forma un ángulo de 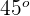 con
con  .
.
1Obtener abscisas
Recordemos que la pendiente de una recta es igual a la tangente del ángulo que forma con el eje 
Es decir 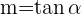
La derivada de  nos indica la pendiente de la recta tangente
nos indica la pendiente de la recta tangente

Como quiero que la recta tangente forme 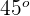 con el eje
con el eje  , estoy pidiendo que la pendiente tenga el valor de
, estoy pidiendo que la pendiente tenga el valor de 
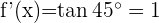
Entonces,
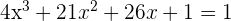
Despejamos
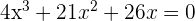
Factorizamos una x

Una solución es

Las otras soluciones se obtienen cuando

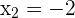

2Obtener ordenadas
Evaluamos los puntos en la función original 
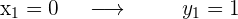
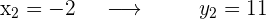
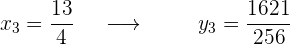
Finalmente

6 ¿En qué punto de la curva  , la tangente es paralela a la cuerda que une los puntos (1, 0) y (e, 1)?
, la tangente es paralela a la cuerda que une los puntos (1, 0) y (e, 1)?
La pendiente de la cuerda tiene que ser igual a la derivada de la función.
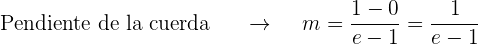
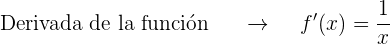
Entonces,

Evaluamos este punto en  para obtener la ordenada
para obtener la ordenada
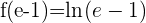
Finalmente

Calcula la ecuación de la recta
7 Calcular la ecuación de la tangente y de la normal a la curva 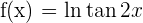 en el punto de abscisa:
en el punto de abscisa: 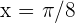 .
.
1 Recta tangente
Obtener pendiente
Derivamos la función, pues sabemos que la derivada nos indica la pendiente de la recta tangente
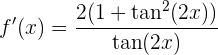
Evaluamos en 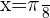
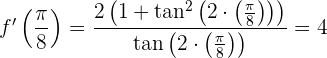
Obtener las coordenadas del punto de tangencia
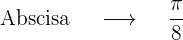
Evaluamos la función original en este punto 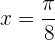 para obtener la ordenada
para obtener la ordenada
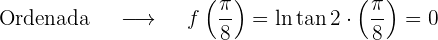
Obtener la ecuación de la recta tangente

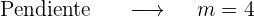

2 Recta normal

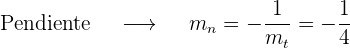
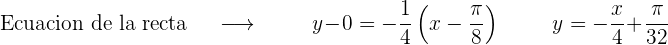
8 Dada la ecuación  , hallar la ecuación de la recta tangente que sea paralela a la recta de ecuación
, hallar la ecuación de la recta tangente que sea paralela a la recta de ecuación  .
.
La ecuación  , al despejar
, al despejar  se puede reescribir
se puede reescribir

Derivando implícitamente la ecuación tenemos:
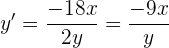
Y como la derivada nos da la pendiente de la recta tangente, la igualaremos a 3 pues es el valor que buscamos que tenga

Tenemos entonces el sistema de ecuaciones de 2x2

Resolvemos, sustituyendo la segunda ecuación en la primera
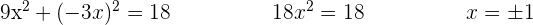
Para obtener la ordenada de los puntos sólo basta con sustituir el valor de  en la ecuación más sencilla del sistema
en la ecuación más sencilla del sistema


Obtenemos la ecuación de la recta en estos puntos
1 x=1

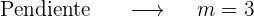

2 x=-1

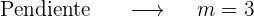
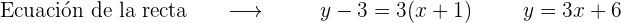
Determina los parámetros
9 Determinar los valores del parámetro b, para qué las tangentes a la curva de la función  en los puntos de abscisas
en los puntos de abscisas  ,
,  sean paralelas.
sean paralelas.
La derivada de  es
es

Para que sean paralelas se tiene que cumplir que las derivadas en  y
y  sean iguales. Es decir
sean iguales. Es decir

Esto es
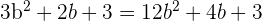

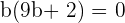
Una solución es

La otra es

10 Hallar los coeficientes de la ecuación  , sabiendo que su gráfica pasa por
, sabiendo que su gráfica pasa por  y por
y por  , y en este último punto su tangente tiene de pendiente
, y en este último punto su tangente tiene de pendiente  .
.
Obtenemos  ecuaciones al sustituir el valor de la abscisa en
ecuaciones al sustituir el valor de la abscisa en  e igualarla al valor de la ordenada de los puntos que pasan por la gráfica
e igualarla al valor de la ordenada de los puntos que pasan por la gráfica
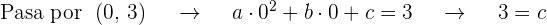
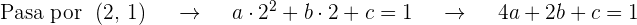
Además la pendiente de la tangente está dada por

Si la pendiente en el punto  es 3, esto quiere decir que
es 3, esto quiere decir que

Resolviendo el sistema de 3x3 se obtiene:
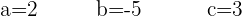
Y la ecuación queda
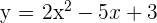
11 La gráfica de la función  pasa por los puntos
pasa por los puntos  y
y 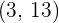 , siendo la tangente a la misma en el punto de abscisa
, siendo la tangente a la misma en el punto de abscisa  paralela a la bisectriz del primer cuadrante. Hallar el valor numérico de
paralela a la bisectriz del primer cuadrante. Hallar el valor numérico de  y
y  .
.
Obtenemos  ecuaciones al sustituir el valor de la abscisa en
ecuaciones al sustituir el valor de la abscisa en  e igualarla al valor de la ordenada de los puntos que pasan por la gráfica
e igualarla al valor de la ordenada de los puntos que pasan por la gráfica

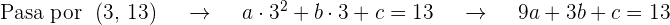
Además la pendiente de la tangente está dada por

Si la pendiente en el punto  es paralela a la bisectriz cuadrante, esto quiere decir que la pendiente es
es paralela a la bisectriz cuadrante, esto quiere decir que la pendiente es 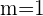
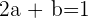
Resolviendo el sistema se obtiene:
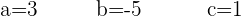
Y la ecuación queda
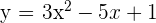
12 Dada la función 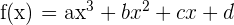 , determina
, determina  y
y  ; sabiendo que la curva pasa por los puntos
; sabiendo que la curva pasa por los puntos  . Además las tangentes en los puntos de abscisa
. Además las tangentes en los puntos de abscisa  y [/latex]-2[/latex] son paralelas al eje
y [/latex]-2[/latex] son paralelas al eje  .
.
Obtenemos  ecuaciones al sustituir el valor de la abscisa en
ecuaciones al sustituir el valor de la abscisa en  e igualarla al valor de la ordenada de los puntos que pasan por la gráfica
e igualarla al valor de la ordenada de los puntos que pasan por la gráfica
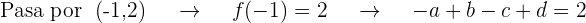
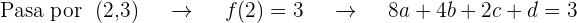
Además la pendiente de la tangente está dada por

Si la pendiente en el punto  es paralela a la bisectriz cuadrante, esto quiere decir que la pendiente es
es paralela a la bisectriz cuadrante, esto quiere decir que la pendiente es 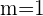


Resolviendo el sistema de 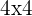 se obtiene:
se obtiene:
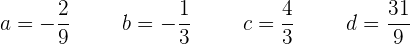
Y la ecuación queda
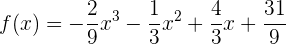
Encuentra el ángulo o área
13 Dada la función 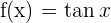 , hallar el ángulo que forma la recta tangente a la gráfica de la función
, hallar el ángulo que forma la recta tangente a la gráfica de la función  en el origen, con el eje de abscisas.
en el origen, con el eje de abscisas.
La recta tangente a la gráfica tiene pendiente

En el origen esta pendiente es

Recodermos que la pendiente de una recta es igual a la tangente del ángulo que forma con el eje 
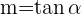
Entonces
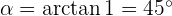
14 Hallar el área del triángulo determinado por los ejes de coordenadas y la tangente a la curva 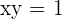 en el punto
en el punto  .
.
Si 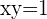 , entonces
, entonces 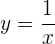
La pendiente de la recta tangente a la curva está dada por la derivada
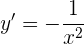
Evaluamos para obtener la pendiente en 
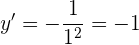
La ordenada del punto se obtiene evaluando en la función original
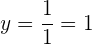
Finalmente
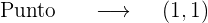
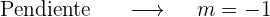
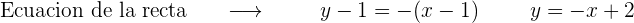
Intersección con el eje OX

Un vértice es 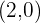
Intersección con el eje OY
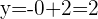
Otro vértice es 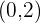
Y la figura es como a continuación
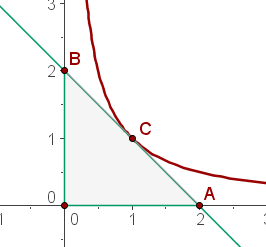
Como es un triángulo rectángulo, su base y altura están dados por los catetos, que en este caso ambos miden  . El área es
. El área es














Apuntes es una plataforma dirigida al estudio y la práctica de las matemáticas a través de la teoría y ejercicios interactivos que ponemos a vuestra disposición. Esta información está disponible para todo aquel/aquella que quiera profundizar en el aprendizaje de esta ciencia. Será un placer ayudaros en caso de que tengáis dudas frente algún problema, sin embargo, no realizamos un ejercicio que nos presentéis de 0 sin que hayáis si quiera intentado resolverlo. Ánimo, todo esfuerzo tiene su recompensa.
Determinar el límite de la función 𝑓(𝑥) =
9
(𝑥+1)
2
cuando la x tiende al infinito
Funcion exponencial
Porque no se puede representar analíticamente la función inversa de F(x) = 1 – 2/x²
F(x)=1-2x resuelvan o expliquenme xfis todos estos f(x)6-x.
F(x)x-2
F(x)3x-1 es para hoy xfis
Un favor me podria ayudar este ejercicio?. Encontrar la funcion inversa f(x) = sen(x/2)
³√(x-3)/3