1 Calcula los puntos en que la tangente a la curva 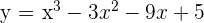 es paralela al eje
es paralela al eje  .
.
Calcula los puntos en que la tangente a la curva 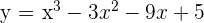 es paralela al eje
es paralela al eje  .
.
El eje  tiene de ecuación
tiene de ecuación  , por tanto
, por tanto 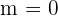
Igualamos la derivada primera a  para hallar los puntos de tangencia
para hallar los puntos de tangencia
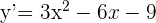 ;
;  (simplificando por
(simplificando por  )
)
Hallamos las segundas coordenadas sustituyendo en la función
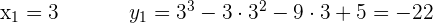


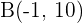
2Se ha trazado una recta tangente a la curva 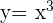 , cuya pendiente es
, cuya pendiente es  y pasa por el punto
y pasa por el punto  . Hallar el punto de tangencia.
. Hallar el punto de tangencia.
Se ha trazado una recta tangente a la curva 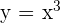 , cuya pendiente es
, cuya pendiente es  y pasa por el punto
y pasa por el punto  . Hallar el punto de tangencia.
. Hallar el punto de tangencia.
Sea el punto de tangencia 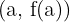

Igualamos la derivada primera a la pendiente

Las ecuaciones de la rectas tangentes son:

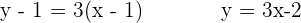


El punto  pertenece a la recta
pertenece a la recta  .
.
Por tanto el punto de tangencia será 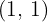 .
.
3Busca los puntos de la curva  , para los cuales la tangente forma un ángulo de
, para los cuales la tangente forma un ángulo de  con
con  .
.
Buscar los puntos de la curva  , para los cuales la tangente forma un ángulo
, para los cuales la tangente forma un ángulo  con
con  .
.

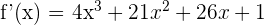
Igualamos la derivada primera a la pendiente y resolvemos la ecuación
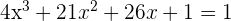
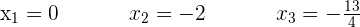
las segundas coordenadas se obtienen sustityendo en la función

4Dada la función  , hallar el ángulo que forma la recta tangente a la gráfica de la función
, hallar el ángulo que forma la recta tangente a la gráfica de la función  en el origen, con el eje de abscisas.
en el origen, con el eje de abscisas.
Dada la función  , hallar el ángulo que forma la recta tangente a la gráfica de la función
, hallar el ángulo que forma la recta tangente a la gráfica de la función  en el origen, con el eje de abscisas.
en el origen, con el eje de abscisas.



5Calcula la ecuación de la tangente y de la normal a la curva 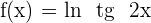 en el punto de abscisa:
en el punto de abscisa: 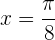 .
.
Calcula la ecuación de la tangente y de la normal a la curva 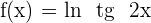 en el punto de abscisa:
en el punto de abscisa: 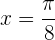 .
.


Ecuación de la tangente:

Ecuación de la normal:

6Hallar los coeficientes de la ecuación  , sabiendo que su gráfica pasa por
, sabiendo que su gráfica pasa por  y por
y por  , y en este último punto su tangente tiene de pendiente
, y en este último punto su tangente tiene de pendiente  .
.
Hallar los coeficientes de la ecuación  , sabiendo que su gráfica pasa por
, sabiendo que su gráfica pasa por  y por
y por  , y en este último punto su tangente tiene de pendiente
, y en este último punto su tangente tiene de pendiente  .
.
Pasa por 
Pasa por 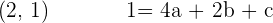

Resolviendo el sistema se obtiene:
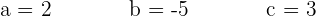
7La gráfica de la función  pasa por los puntos
pasa por los puntos  y
y 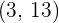 . siendo la tangente a la misma en el punto de abscisa
. siendo la tangente a la misma en el punto de abscisa  paralela a la bisectriz del primer cuadrante. Hallar el valor numérico de
paralela a la bisectriz del primer cuadrante. Hallar el valor numérico de  y
y  .
.
La gráfica de la función  pasa por los puntos
pasa por los puntos  y
y 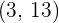 . siendo la tangente a la misma en el punto de abscisa
. siendo la tangente a la misma en el punto de abscisa  paralela a la bisectriz del primer cuadrante. Hallar el valor numérico de
paralela a la bisectriz del primer cuadrante. Hallar el valor numérico de  y
y  .
.
Pasa por 
Pasa por 

Resolviendo el sistema se obtiene:
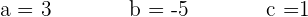
8Dada la función 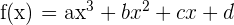 , determina
, determina  y
y  ; sabiendo que la curva pasa por los puntos
; sabiendo que la curva pasa por los puntos 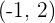 y
y  , y que las tangentes a ellas en los puntos de abscisa
, y que las tangentes a ellas en los puntos de abscisa  y
y  son paralelas al ejes de abscisas.
son paralelas al ejes de abscisas.
Dada la función 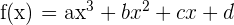 , determina
, determina  y
y  ; sabiendo que la curva pasa por los puntos
; sabiendo que la curva pasa por los puntos 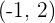 y
y  , y que las tangentes a ellas en los puntos de abscisa
, y que las tangentes a ellas en los puntos de abscisa  y
y  son paralelas al ejes de abscisas.
son paralelas al ejes de abscisas.
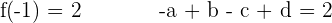
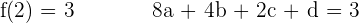
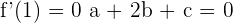
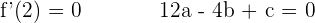
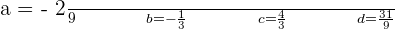
9¿En qué punto de la curva  , la tangente es paralela a la cuerda que une los puntos
, la tangente es paralela a la cuerda que une los puntos  y
y 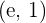 ?
?
¿En qué punto de la curva  , la tangente es paralela a la cuerda que une los puntos
, la tangente es paralela a la cuerda que une los puntos  y
y 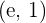 ?
?
La pendiente de la cuerda tiene que ser igual a la derivada de la función.
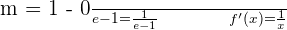

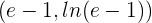
10La ecuación de un movimiento circular es: 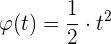 . ¿Cuál es la velocidad y la aceleración angulares al cabo de siete segundos?
. ¿Cuál es la velocidad y la aceleración angulares al cabo de siete segundos?
La ecuación de un movimiento circular es: 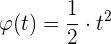 . ¿Cuál es la velocidad y la aceleración angulares al cabo de siete segundos?
. ¿Cuál es la velocidad y la aceleración angulares al cabo de siete segundos?
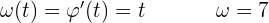
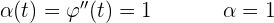
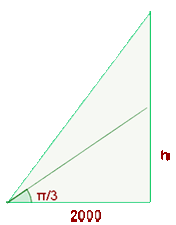
11Un observador se encuentra a  de la torre de lanzamiento de un cohete. Cuando éste despega verticalmente mide la variación del ángulo
de la torre de lanzamiento de un cohete. Cuando éste despega verticalmente mide la variación del ángulo  que forma la línea visual que le une con el cohete y la del suelo horizontal en función del tiempo transcurrido. Sabiendo que
que forma la línea visual que le une con el cohete y la del suelo horizontal en función del tiempo transcurrido. Sabiendo que 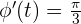 , se pide:
, se pide:
a ¿Cuál es la altura del cohete cuando 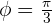 radianes?
radianes?
b ¿Cuál es la velocidad del cohete cuando 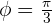 radianes?
radianes?
Un observador se encuentra a  de la torre de lanzamiento de un cohete. Cuando éste despega verticalmente mide la variación del ángulo
de la torre de lanzamiento de un cohete. Cuando éste despega verticalmente mide la variación del ángulo  que forma la línea visual que le une con el cohete y la del suelo horizontal en función del tiempo transcurrido. Sabiendo que
que forma la línea visual que le une con el cohete y la del suelo horizontal en función del tiempo transcurrido. Sabiendo que 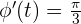 , se pide:
, se pide:
a ¿Cuál es la altura del cohete cuando 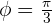 radianes?
radianes?

b ¿Cuál es la velocidad del cohete cuando 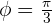 radianes?
radianes?

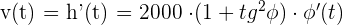

12Se bombea gas a un globo esférico a razón de 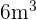 /min. Si la presión se mantiene constante. ¿Cuál es la velocidad con la que cambia el radio del globo cuando el diámetro mide
/min. Si la presión se mantiene constante. ¿Cuál es la velocidad con la que cambia el radio del globo cuando el diámetro mide 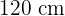 ?
?
Se bombea gas a un globo esférico a razón de 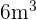 /min. Si la presión se mantiene constante. ¿Cuál es la velocidad con la que cambia el radio del globo cuando el diámetro mide
/min. Si la presión se mantiene constante. ¿Cuál es la velocidad con la que cambia el radio del globo cuando el diámetro mide 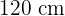 ?
?
Para resolver este problema necesitamos la fórmula del volumen en términos del radio:

Además, sabemos que la tasa de cambio del volumen es 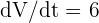 con unidades de
con unidades de  .
.
Para poder relacionar las funciones necesitamos escribir al volumen en términos del tiempo. Esto lo haremos escribiendo 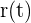 , ya que el radio también varía con el tiempo. De este modo:
, ya que el radio también varía con el tiempo. De este modo:

Ahora derivamos el volumen respecto al tiempo (utilizaremos la regla de la cadena):

Observemos que en la ecuación anterior ya tenemos todo lo que necesitamos. Ya conocemos 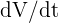 , el cual es constante. Asimismo,
, el cual es constante. Asimismo,  es la variable que buscamos. Despejamos primero
es la variable que buscamos. Despejamos primero 
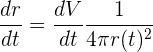
No sabemos el tiempo, pero sabemos que el diámetro es 120 cm, es decir, el radio es 60 cm o 0.6 m. Sustituimos esos valores:

Por lo tanto, la respuesta es 1.33 m/min.
13Hallar el ángulo de intersección entre las curvas 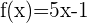 y
y 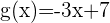
Hallar el ángulo de intersección entre las curvas 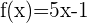 y
y 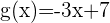
1Aplicamos la fórmula

2Igualamos ambas curvas
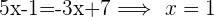
3Calculamos las pendientes
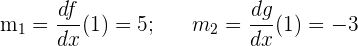
4Sustituimos en la fórmula del ángulo entre dos curvas
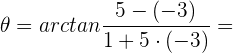



Apuntes es una plataforma dirigida al estudio y la práctica de las matemáticas a través de la teoría y ejercicios interactivos que ponemos a vuestra disposición. Esta información está disponible para todo aquel/aquella que quiera profundizar en el aprendizaje de esta ciencia. Será un placer ayudaros en caso de que tengáis dudas frente algún problema, sin embargo, no realizamos un ejercicio que nos presentéis de 0 sin que hayáis si quiera intentado resolverlo. Ánimo, todo esfuerzo tiene su recompensa.
Y=x³ x=1 ∆x=0.02
Dy= 3x^2 • dx
dy= 3(1)^2 • 0.02
dy= 0.06
Considera la curva de ecuación y=-X³ + 26X y halla sus rectas tangentes que sean paralelas a la recta y= -X.
f(x)= 4x-2
hola me pode hayudar con este problema Realizar la derivada por definición de f(x) = x³+1 en x = 0.
De acuerdo con la definición de derivada de una función
f´(x)=〖lim〗┬(h→0)〖(f(x+h)-f(x))/h〗
Calcular la derivada de las siguientes funciones siguiendo el proceso del límite:
f(x)=1/2 x^3+2x+3
4(x+h)-4x/h =4x+4h-4x/h= 4h/h= 4