Vamos a estudiar la indeterminación del tipo cero partido cero en dos casos.
Caso 1: Función racional
Este caso aplica cuando tenemos una fracción donde el numerador y el denominador son polinomios.
A continuación se explican el procedimiento para obtener el límite cuando tienes una indeterminación del tipo cero entre cero.
1 Al intentar calcular el límite, se identifica la indeterminación del tipo cero sobre cero
2 Se descomponen en factores los polinomios de el numerador y denominador
3 Se simplifica la fracción
4 Se calcula el límite de la expresión simplificada
Ejemplos
1 Si intentamos obtener el límite, veremos que es del tipo 0/0
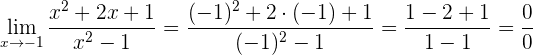
2 Factorizamos
El numerador es un trinomio cuadrado perfecto que lo podemos escribirlo como un binomio al cuadrado.
El denominador es una diferencia de cuadrados que es igual al producto de binomios conjugados. Esto es
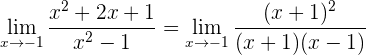
3 Simplificamos la fracción
4 Ahora calculamos el límite
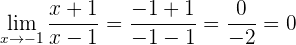
El límite es 0
1 Si intentamos obtener el límite, veremos que es del tipo 0/0
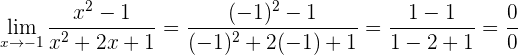
2 Factorizamos
El numerador es una diferencia de cuadrados que es igual al producto de binomios conjugados.
El denominador es un trinomio cuadrado perfecto que lo podemos escribirlo como un binomio al cuadrado. Esto es
3 Simplificamos la fracción
4 Ahora calculamos el límite
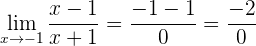
Como obtuvimos cero solamente en el denominador, debemos identificar si este límite va a infinito positivo, negativo o no tiene límite (por un lado se va a infinito positivo y por el otro, negativo). Para esto tomamos límites laterales
Límite por la izquierda
Si le damos a la 
un valor que se acerque a 
por la izquierda como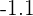 
; tanto el numerador como denominador son negativos, por tanto el límite por la izquierda será: 
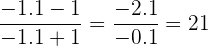
Límite por la derecha
Si le damos a la un valor que se acerque a −1 por la derecha como −0,9. El numerador será negativo y el denominador positivo, por tanto el límite por la derecha será: 
Como el límite por la izquierda y derecha no son iguales se concluye que no existe el límite en x = −1
Caso 2: Función con radicales
Este caso aplica cuando tenemos una fracción que tiene un radical, generalmente en el denominador.
A continuación se explica el procedimiento para obtener el límite cuando tienes una indeterminación del tipo cero entre cero.
1 Al intentar calcular el límite, se identifica la indeterminación del tipo cero sobre cero
2 Multiplicamos numerador y denominador por el conjugado de la expresión irracional.
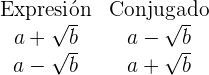
Ejemplo:
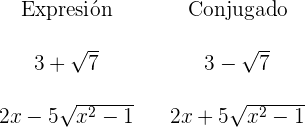
3 Se realizan las operaciones y se simplifica la fracción
Toma en cuenta que una expresión irracional multiplicada por su conjugado, da como resultado una diferencia de cuadrados
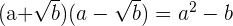
Ejemplo:
4 Se calcula el límite de la expresión simplificada
Ejemplo
1 Al intentar calcular el límite, se identifica la indeterminación del tipo cero sobre cero
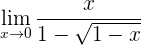
2 Multiplicamos y dividimos por el conjugado del denominador
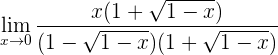
3 Realizamos las operaciones y simplificamos la fracción.
En el denominador tenemos una suma por diferencia (binomios conjugados) que será igual a diferencia de cuadrados
4 Calculamos el límite
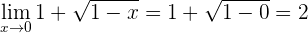
El límite es 2
¿Te ha gustado este artículo? ¡Califícalo!
Cargando...
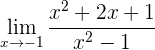
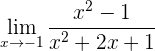
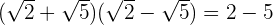
Apuntes es una plataforma dirigida al estudio y la práctica de las matemáticas a través de la teoría y ejercicios interactivos que ponemos a vuestra disposición. Esta información está disponible para todo aquel/aquella que quiera profundizar en el aprendizaje de esta ciencia. Será un placer ayudaros en caso de que tengáis dudas frente algún problema, sin embargo, no realizamos un ejercicio que nos presentéis de 0 sin que hayáis si quiera intentado resolverlo. Ánimo, todo esfuerzo tiene su recompensa.
Determinar el límite de la función 𝑓(𝑥) =
9
(𝑥+1)
2
cuando la x tiende al infinito
Funcion exponencial
Porque no se puede representar analíticamente la función inversa de F(x) = 1 – 2/x²
F(x)=1-2x resuelvan o expliquenme xfis todos estos f(x)6-x.
F(x)x-2
F(x)3x-1 es para hoy xfis
Un favor me podria ayudar este ejercicio?. Encontrar la funcion inversa f(x) = sen(x/2)
³√(x-3)/3