Capítulos
En ocasiones nos encontramos con que una función tiene una indeterminación de infinito dividido por infinito. Es decir, consideremos la función
tal que 
y 
. Así, nuestra función evaluada en 
sería
En este caso, decimos que la función está indeterminada en , pues no es posible asignarle valor alguno a 
. Sin embargo, podemos utilizar alguno de los siguientes dos métodos para encontrar el límite de la función en —observemos que el límite en no es lo mismo que el valor de —:
Primer método: comparación del orden de los polinomios
Estos métodos sólo funcionan con funciones racionales de la forma
en donde 
y 
son polinomios y algunos casos muy particulares como exponenciales y radicales. Cuando no se tienen estos casos, existen otros métodos como la regla de L'Hôpital.
El primer método consiste en comparar los grados de y :
El numerador tiene mayor grado que el denominador
Si el numerador tiene mayor grado que el denominador, entonces el límite será 
o 
. El signo del límite será el mismo signo que tiene la división de los coeficientes de mayor grado. En el segundo ejemplo de abajo, observemos que el límite es porque la división de los coeficientes es 
; es decir, tiene signo negativo.
El grado del denominador es mayor al grado del numerador
es mayor al grado del numerador, entonces el límite siempre será 0. 
El numerador y el denominador tienen el mismo grado
Si el numerador y denominador tienen el mismo grado, entonces el límite es el cociente de los coeficientes de mayor grado. Observemos el ejemplo de abajo. El numerador tiene coeficiente principal 2, mientras que el denominador tiene coeficiente principal 3. Por lo tanto, como ambos polinomios tienen el mismo grado, entonces el límite es 
.
Casos particulares del método de comparación
Dada una función
existen casos donde podemos comparar a 
y 
de manera similar a como comparamos los polinomios. Estos casos involucran funciones exponenciales y funciones radicales.
1 Si o son exponenciales, entonces podemos pensar que su grado siempre es mayor al de cualquier polinomio (formalmente se dice que una exponencial es de mayor orden que un polinomio). Si tanto el numerador como el denominador son exponenciales, entonces tendrá mayor orden la exponencial con la base más grande.
2 Si el numerador o el denominador es un radical de la forma
,
entonces consideramos que su grado es 
y su coeficiente de mayor grado es 
.
Segundo método: dividir por una misma función el numerador y denominador
Dado que
entonces podemos multiplicar y dividir una función por con el fin de calcular el límite de forma más sencilla. Esto debido a que
Cociente de polinomios
Si se trata de cociente de polinomios, entonces dividimos ambos polinomios por la potencia de mayor grado. Por ejemplo, si tenemos
Dividimos cada polinomio por 
, simplificamos las fracciones y aplicamos el límite:
Es importante que tomemos en cuenta el signo de los coeficientes de mayor grado del numerador y denominador, pues esto puede cambiar el signo del infinito. Al igual que con el método anterior, el signo será el mismo que el cociente de los coeficientes de mayor grado.
Funciones exponenciales
Si son funciones exponenciales, entonces dividimos por la exponencial de mayor base. Observemos el siguiente ejemplo:
Primero aplicamos las propiedades del producto y del cociente de potencias, con el fin de quitar las sumas o restas de los exponentes:
Dividimos el numerador y el denominador por
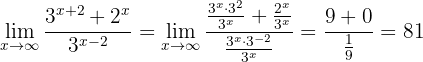
Ejemplos de la indeterminación infinito dividido por infinito
Vamos a resolver algunos ejemplos para poner en práctica lo que acabamos de ver.
El resultado es 
ya que el numerador es de orden mayor que el denominador.
Ahora tenemos un denominador con orden superior al del numerador. Por lo tanto, el límite es 0.
En este caso tenemos una función radical en el numerador. Por lo tanto, suponemos que su grado es 
. Por consiguiente, debido a que 
, entonces el límite es 0.
4
Como mencionamos anteriormente, las funciones exponenciales siempre tienen mayor orden que los polinomios —aunque este sea de grado 23—. Por tanto, el límite es .
¿Te ha gustado este artículo? ¡Califícalo!
Cargando...
Apuntes es una plataforma dirigida al estudio y la práctica de las matemáticas a través de la teoría y ejercicios interactivos que ponemos a vuestra disposición. Esta información está disponible para todo aquel/aquella que quiera profundizar en el aprendizaje de esta ciencia. Será un placer ayudaros en caso de que tengáis dudas frente algún problema, sin embargo, no realizamos un ejercicio que nos presentéis de 0 sin que hayáis si quiera intentado resolverlo. Ánimo, todo esfuerzo tiene su recompensa.
Nose como se arrastra la imagen
Hola, nos encantaría poder ayudarte pero podrías mencionar el número del ejercicio y te diremos como puedes arrastrar la imagen al lugar que deseas.
Representar gráficamente la curva Inversión Ahorro cuando hay una política fiscal de incremento del gasto público
la uno esta mal el vertice no es (0,0) es (0,3)
Una disculpa ya se corrigió.