Temas
- Dominio en funciones polinómicas
- Calcula el dominio de las siguientes funciones racionales
- Calcular el dominio de las funciones radicales
- Calcular el dominio de las funciones exponenciales
- Calcular el dominio de las funciones logarítmicas
- Calcular el dominio de las funciones trigonométricas
- Funciones radicales y su dominio
- Calcular el dominio de la función
- Calcular el dominio de la función definida a trozos
Recordemos que, el dominio de una función o conjunto de salida se refiere a: todos los valores que se le pueden asignar a la variable independiente sin que la función se indetermine. Aquí, estudiaremos el dominio de funciones reales, es decir, funciones cuyo dominio e imagen son los números reales o subconjuntos de ellos.
Dominio en funciones polinómicas
1 
2 
3 
Calcular el dominio de las funciones polinómicas:
El dominio de una función polinómica entera es 
, es decir, todos los números reales.
1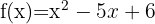
2 
3
Note que esta es una función polinómica con coeficientes racionales:
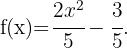Por lo tanto,
Calcula el dominio de las siguientes funciones racionales
1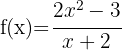 
2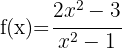 
3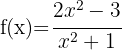 
4 
5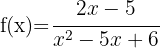
6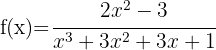 
7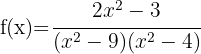 
El dominio de una función racional es 
menos los valores que anulan el denominador. Para encontrar el dominio, debemos igualar el denominador a cero y resolver la ecuación. Las soluciones a dicha ecuación son los puntos que no pertenecen al dominio, ya que anulan el denominador.
1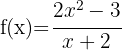
2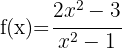
3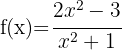
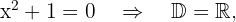
porque esta ecuación no tiene raíces reales.
4
porque la raíz es doble.
5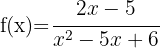
Tenemos que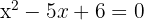 
, entonces
Así, 
o 
. Por lo tanto, el dominio es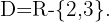 
6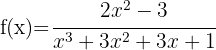
Observamos que el polinomio es el desarrollo de un binomio al cubo 
porque 
es una raíz triple.
7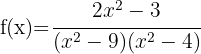
Factorizando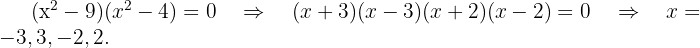 
Por lo tanto,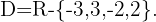 
Calcular el dominio de las funciones radicales
1 
2 
3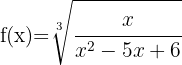 
El dominio de una función irracional de índice impar es
1
2
El dominio de esta función son todos los reales menos los valores donde se anula el denominador de la función racional dentro de la raíz cúbica. Así,
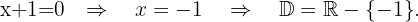
3
El dominio de esta función son todos los reales menos los valores donde se anula el denominador de la función racional dentro de la raíz cúbica. Así,
Calcular el dominio de las funciones exponenciales
1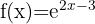 
2 
El dominio de una función exponencial es
1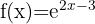
2
Como el exponente es racional, 
no pertenece al dominio porque anula al denominador. Por lo tanto, 
.
Calcular el dominio de las funciones logarítmicas
1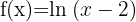 
2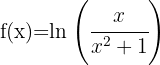 
Para que la función logoritmo esté bien definida, su argumento debe ser positivo, es decir, su dominio es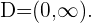 
1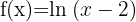
Resolvemos 
2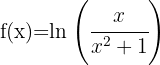
Como el denominador es siempre positivo, solo estudiamos el numerador. Así
.
Calcular el dominio de las funciones trigonométricas
1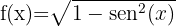 
2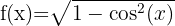 
El dominio de una función irracional de índice par está formado por el conjunto los valores que hacen que el radicando sea mayor o igual a cero Las funciones trigonométricas seno y coseno tienen como dominio a todos los números reales. Además, su valor máximo es 1, por lo se tiene que éstas funciones siempre tienen valores menores o iguales a 1 para todo número real.
1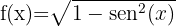
Resolvemos 
2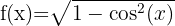
Resolvemos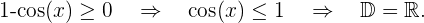 
Funciones radicales y su dominio
1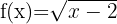 
2 
3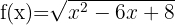 
4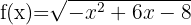 
5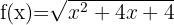 
6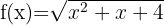 
7 
8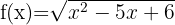 
9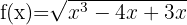 
10
11 
12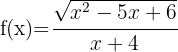 
13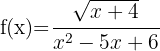
14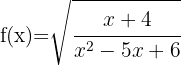 
El dominio de una función irracional de índice par está formado por el conjunto los valores que hacen que el radicando sea mayor o igual a cero.
1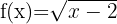
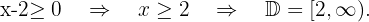
2
Resolvemos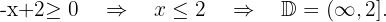 
3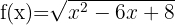
Resolvemos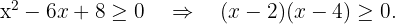 
Igualamos a cero para obtener las raíces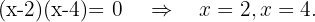 
Finalmente, tomamos los intervalos en los que la desigualdad es positiva. La unión de estos será nuestro dominio. Por lo tanto 
4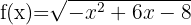
Resolvemos 
Igualamos a cero para obtener las raíces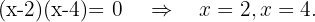
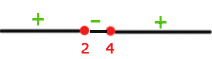
Finalmente, tomamos los intervalos en los que la desigualdad es negativa. La unión de estos será nuestro dominio. Por lo tanto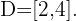 
5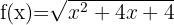
Resolvemos 
porque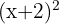 
siempre es mayor o igual a cero.
6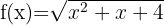
Resolvemos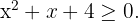 
Si igualamos a cero, la ecuación correspondiente no tiene soluciones reales. Además, notamos que, si tomamos cualquier valor será positivo o cero. Por lo tanto,
7
Resolvemos 
Observe que, esta desigualdad solo se cumple para el valor 
ya que para todos los demás valores de 
, el resultado es siempre negativo. Así, es el único valor que satisface nuestra desigualdad y por lo tanto, 
8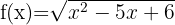
Resolvemos la desigualdad de segundo grado
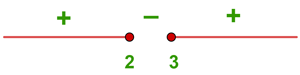
Finalmente, tomamos los intervalos en los que la desigualdad es positiva con los extremos donde se anula incluidos. La unión de estos intervalos será nuestro dominio. Por lo tanto,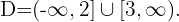 
9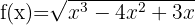 
Resolvemos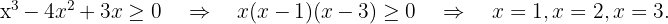 
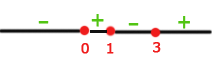
Finalmente, tomamos los intervalos en los que la desigualdad es positiva con los extremos donde se anula incluidos. La unión de estos intervalos será nuestro dominio. Por lo tanto,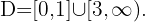 
10
Por estar la raíz en el denominador, el radicando tiene que ser mayor que cero, pero no igual porque entonces anularía el denominador. Resolvemos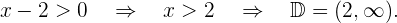 
11
En este caso se tiene que cumplir que el denominador sea distinto de cero y la raíz del numerador mayor o igual que cero. Resolvemos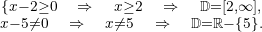 
La solución es la intersección de los dos conjuntos, por lo tanto,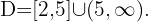 
12 
El numerador tiene que se mayor o igual que cero y el denominador distinto de cero. Resolvemos 
La solución es la intersección de los dos conjuntos, por lo tanto, 
13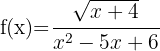
El denominador tiene que ser mayor que cero. Resolvemos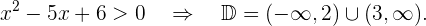 
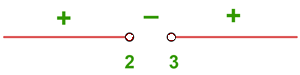
14
El radicando tiene que ser mayor que cero y el denominador distinto de cero. Resolvemos 
y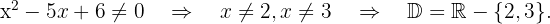 
La solución es la intersección de los dos conjuntos, por lo tanto,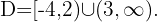 
Calcular el dominio de la función
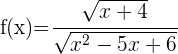
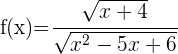
Resolvemos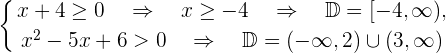 
La solución es la intersección de los dos conjuntos, por lo tanto,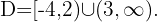
Calcular el dominio de la función definida a trozos
En el primer trozo se tiene que cumplir que el denominador sea distinto de cero. En el segundo trozo al ser 3 una constante siempre será positivo, solo estudiamos que el denominador sea mayor que cero. Así,
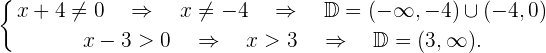
Finalmente, la solución es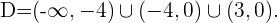 
¿Estás buscando un profesor de mates? En Superprof encontrarás a tu profe ideal, ya prefieras un profesor de matematicas online o uno que se desplace a domicilio.
¿Te ha gustado este artículo? ¡Califícalo!
Cargando...
Apuntes es una plataforma dirigida al estudio y la práctica de las matemáticas a través de la teoría y ejercicios interactivos que ponemos a vuestra disposición. Esta información está disponible para todo aquel/aquella que quiera profundizar en el aprendizaje de esta ciencia. Será un placer ayudaros en caso de que tengáis dudas frente algún problema, sin embargo, no realizamos un ejercicio que nos presentéis de 0 sin que hayáis si quiera intentado resolverlo. Ánimo, todo esfuerzo tiene su recompensa.
Determinar el límite de la función 𝑓(𝑥) =
9
(𝑥+1)
2
cuando la x tiende al infinito
Funcion exponencial
Porque no se puede representar analíticamente la función inversa de F(x) = 1 – 2/x²
F(x)=1-2x resuelvan o expliquenme xfis todos estos f(x)6-x.
F(x)x-2
F(x)3x-1 es para hoy xfis
Un favor me podria ayudar este ejercicio?. Encontrar la funcion inversa f(x) = sen(x/2)
³√(x-3)/3