Temas
- Representa las siguientes rectas
- Representa las siguientes funciones, sabiendo que:
- Problemas de representación de funciones
- Halla el vértice y la ecuación del eje de simetría de las siguientes parábolas:
- Indica, sin dibujarlas, en cuantos puntos cortan al eje de abscisas las siguientes parábolas:
- Representa gráficamente las funciones cuadráticas:
- Calcula los siguientes valores de funciones cuadráticas
¡Bienvenidos a nuestra página dedicada a ejercicios resueltos de gráficas de funciones! Si estás interesado en comprender cómo las funciones matemáticas se pueden visualizar y analizar gráficamente, has llegado al lugar indicado.
En este espacio, exploraremos conceptos clave relacionados con la representación gráfica de funciones lineales y cuadráticas. Te proporcionaremos una variedad de ejercicios prácticos y explicaciones paso a paso para ayudarte a desarrollar tus habilidades en este fascinante campo.
En estos ejercicios necesitarás gráficar o analizar gráficas de funciones para extraer información fundamental sobre su comportamiento, una combinación que sin duda te convertirá en todo un experto en esta área. ¡Échate un clavado a estos interesantes ejercicios!
Representa las siguientes rectas
1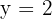
2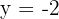
3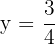
4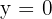
5
6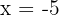
7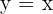
8
9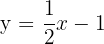
10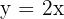
1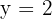

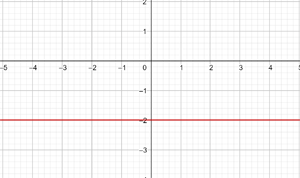
2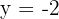
3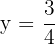
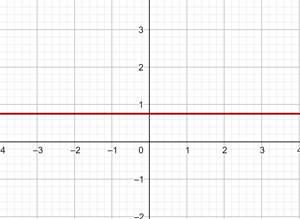
4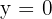
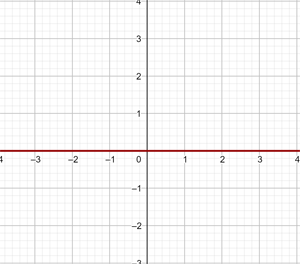
5
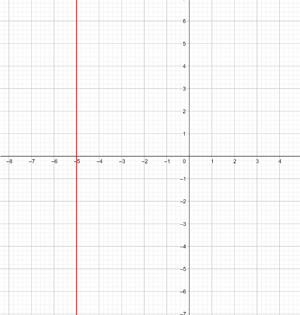
6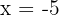
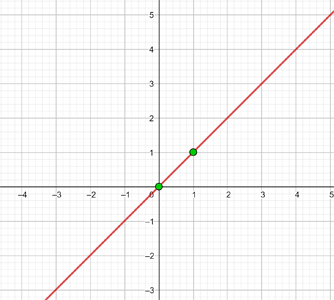
7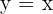
 | 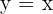 |
|---|---|
 |  |
 |  |
8

 |  |
|---|---|
 |  |
 |  |
9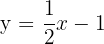
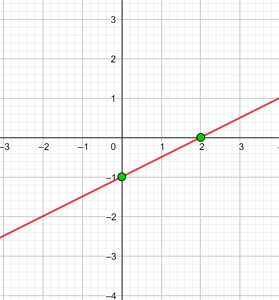
 | 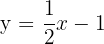 |
|---|---|
 |  |
 |  |
10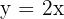
 |  |
|---|---|
 |  |
 |  |
Representa las siguientes funciones, sabiendo que:
1Tiene pendiente  y ordenada en el origen
y ordenada en el origen  .
.
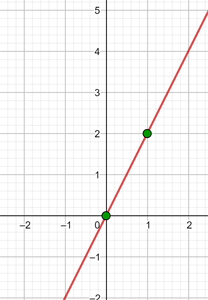
2Tiene por pendiente  y pasa por el punto
y pasa por el punto 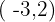 .
.
3Pasa por los puntos 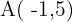 y
y  .
.
4Pasa por el punto 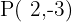 y es paralela a la recta de ecuación
y es paralela a la recta de ecuación 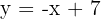 .
.
Representa las siguientes funciones, sabiendo que:
1 Tiene pendiente  y ordenada en el origen
y ordenada en el origen  .
.
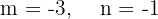
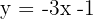

 | 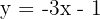 |
|---|---|
 |  |
 |  |
2 Tiene por pendiente  y pasa por el punto (−3, 2).
y pasa por el punto (−3, 2).
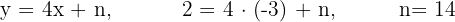
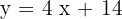

 |  |
|---|---|
 |  |
 |  |
3Pasa por los puntos 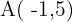 y
y  .
.
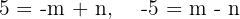

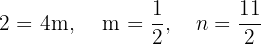


 | 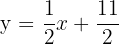 |
|---|---|
 | 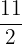 |
 |  |
4Pasa por el punto 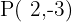 y es paralela a la recta de ecuación
y es paralela a la recta de ecuación 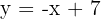 .
.

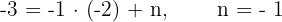


 | 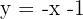 |
|---|---|
 |  |
 |  |
Problemas de representación de funciones
1Tres kilogramos de boquerones valen  €. Escribe y representa la función que define el coste de los boquerones en función de los kilogramos comprados.
€. Escribe y representa la función que define el coste de los boquerones en función de los kilogramos comprados.
 €. Escribe y representa la función que define el coste de los boquerones en función de los kilogramos comprados.
€. Escribe y representa la función que define el coste de los boquerones en función de los kilogramos comprados. La ordenada al origen es  que corresponde al valor de
que corresponde al valor de  kilogramos.
kilogramos.
La pendiente es 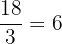
La ecuación de la recta es 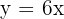

2En las  primeras semanas de cultivo de una planta, que medía
primeras semanas de cultivo de una planta, que medía  cm, se ha observado que su crecimiento es directamente proporcional al tiempo, viendo que en la primera semana ha pasado a medir
cm, se ha observado que su crecimiento es directamente proporcional al tiempo, viendo que en la primera semana ha pasado a medir  cm. Establecer una función a fin que dé la altura de la planta en función del tiempo y representar gráficamente.
cm. Establecer una función a fin que dé la altura de la planta en función del tiempo y representar gráficamente.
 primeras semanas de cultivo de una planta, que medía
primeras semanas de cultivo de una planta, que medía  cm, se ha observado que su crecimiento es directamente proporcional al tiempo, viendo que en la primera semana ha pasado a medir
cm, se ha observado que su crecimiento es directamente proporcional al tiempo, viendo que en la primera semana ha pasado a medir  cm. Establecer una función a fin que dé la altura de la planta en función del tiempo y representar gráficamente.
cm. Establecer una función a fin que dé la altura de la planta en función del tiempo y representar gráficamente. Altura inicial  cm es la ordenada al origen
cm es la ordenada al origen
Crecimiento semanal 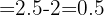 es la pendiente
es la pendiente
La ecuación de la recta es 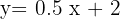

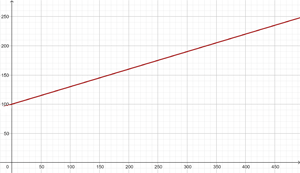
3Por el alquiler de un coche cobran  € diarios más
€ diarios más  € por kilómetro. Encuentra la ecuación de la recta que relaciona el coste diario con el número de kilómetros y represéntala. Si en un día se ha hecho un total de
€ por kilómetro. Encuentra la ecuación de la recta que relaciona el coste diario con el número de kilómetros y represéntala. Si en un día se ha hecho un total de  km, ¿qué importe debemos abonar?
km, ¿qué importe debemos abonar?
 € diarios más
€ diarios más  € por kilómetro. Encuentra la ecuación de la recta que relaciona el coste diario con el número de kilómetros y represéntala. Si en un día se ha hecho un total de
€ por kilómetro. Encuentra la ecuación de la recta que relaciona el coste diario con el número de kilómetros y represéntala. Si en un día se ha hecho un total de  km, ¿qué importe debemos abonar?
km, ¿qué importe debemos abonar? La ordenada al origen es  y la pendiente es
y la pendiente es 
La ecuación de la recta es 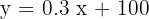
La cantidad a pagar por recorrer  km en un día es:
km en un día es:
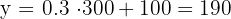 €
€
4Un salón de eventos ofrece sus servicios en un único plan para  personas a un costo de
personas a un costo de  €. Además, la política del salón dice que si las
€. Además, la política del salón dice que si las  personas son sobrepasadas, se cobrará
personas son sobrepasadas, se cobrará  € por persona extra. Escribe y representa la función que define estos costes. Utiliza esta función para calcular un sobrecupo de
€ por persona extra. Escribe y representa la función que define estos costes. Utiliza esta función para calcular un sobrecupo de  personas.
personas.
 personas a un costo de
personas a un costo de  €. Además, la política del salón dice que si las
€. Además, la política del salón dice que si las  personas son sobrepasadas, se cobrará
personas son sobrepasadas, se cobrará  € por persona extra. Escribe y representa la función que define estos costes. Utiliza esta función para calcular un sobrecupo de
€ por persona extra. Escribe y representa la función que define estos costes. Utiliza esta función para calcular un sobrecupo de  personas.
personas. Como sabemos que el plan tiene un coste de  € independientemente si son
€ independientemente si son  o menos personas, entonces estamos ante la función constante
o menos personas, entonces estamos ante la función constante

Ahora, por cada persona extra, el salón cobra  €. Esto es, después de
€. Esto es, después de  personas, nuestra función deja de ser constante y se convierte en una función lineal cuya pendiente es de
personas, nuestra función deja de ser constante y se convierte en una función lineal cuya pendiente es de  , la cual corresponde al costo extra por persona. Así, nuestra función, la cual tiene como variable independiente a las personas extras, es
, la cual corresponde al costo extra por persona. Así, nuestra función, la cual tiene como variable independiente a las personas extras, es
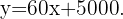
Como podemos comprobar facilmente,  €, que corresponde a
€, que corresponde a  personas y
personas y
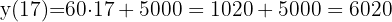
euros que corresponde al coste total para un sobrecupo de  personas.
personas.
5Una casa en la playa, con disponibilidad para  personas, tiene un coste por noche de
personas, tiene un coste por noche de 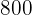 €. Además, se requiere una reservación de un mínimo de
€. Además, se requiere una reservación de un mínimo de  noches con una opción abierta para alquilar la propiedad
noches con una opción abierta para alquilar la propiedad  noches más con costo de
noches más con costo de  € cada una. Escribe y representa la función que modela esta situación. Un grupo de amigos decide alquilar la propiedad y desean extender su estancia
€ cada una. Escribe y representa la función que modela esta situación. Un grupo de amigos decide alquilar la propiedad y desean extender su estancia  noches más. ¿Cuánto deberán pagar en total?
noches más. ¿Cuánto deberán pagar en total?
5Una casa en la playa, con disponibilidad para  personas, tiene un coste por noche de
personas, tiene un coste por noche de 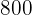 €. Además, se requiere una reservación de un mínimo de
€. Además, se requiere una reservación de un mínimo de  noches con una opción abierta para alquilar la propiedad
noches con una opción abierta para alquilar la propiedad  noches más con costo de
noches más con costo de  € cada una. Escribe y representa la función que modela esta situación. Un grupo de amigos decide alquilar la propiedad y desean extender su estancia
€ cada una. Escribe y representa la función que modela esta situación. Un grupo de amigos decide alquilar la propiedad y desean extender su estancia  noches más. ¿Cuánto deberán pagar en total?
noches más. ¿Cuánto deberán pagar en total?
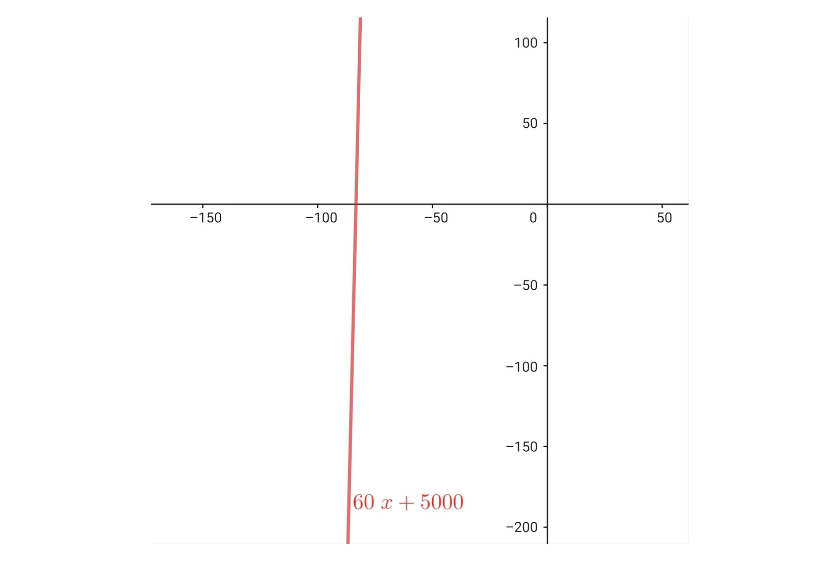
El mínimo de noches que se requieren al alquilar la propiedad son  . Si cada noche tiene un costo de
. Si cada noche tiene un costo de 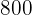 €, el total para la reservación de
€, el total para la reservación de  es de
es de  €. Esto se puede modelar con la función constante
€. Esto se puede modelar con la función constante
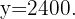
Cada noche extra tiene un costo de  €. Para incorporar este factor, debemos pasar a una función lineal. La función lineal
€. Para incorporar este factor, debemos pasar a una función lineal. La función lineal
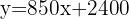
modela nuestro problema. Aquí la variable independiente 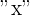 corresponde al número de noches extras.
corresponde al número de noches extras.
Si el grupo de amigos decide extender su estadia en la casa  noches, entonces esto corresponde a
noches, entonces esto corresponde a
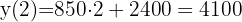 €
€
como coste total por las  noches.
noches.

Halla el vértice y la ecuación del eje de simetría de las siguientes parábolas:
1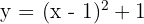
2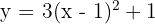
3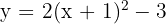
4
5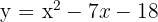
6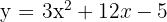
Halla el vértice y la ecuación del eje de simetría de las siguientes parábolas:
1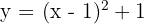
Vértice 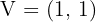
Eje de simetría 
2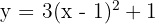
Vértice 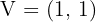
Eje de simetría 
3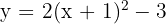
Vértice 
Eje de simetría 
4
Vértice 
Eje de simetría 
5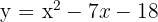
Vértice 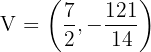
Eje de simetría 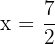
6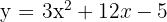
Vértice 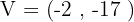
Eje de simetría 
Indica, sin dibujarlas, en cuantos puntos cortan al eje de abscisas las siguientes parábolas:
1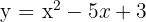
2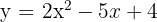
3
4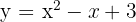
Indica, sin dibujarlas, en cuantos puntos cortan al eje de abscisas las siguientes parábolas:
1 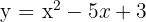
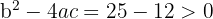
Dos puntos de corte
2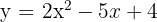

No hay puntos de corte
3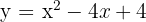
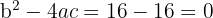
Un punto de corte
4

Dos puntos de corte
Representa gráficamente las funciones cuadráticas:
1
2
Representa gráficamente las funciones cuadráticas:
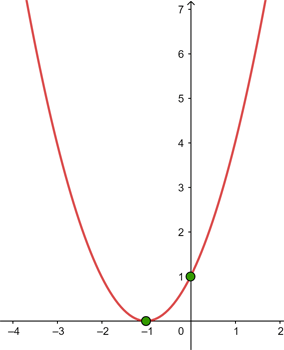
1
Calculamos las coordenadas del vértice
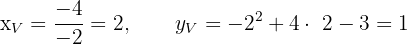
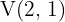
Buscamos los puntos de corte con el eje 
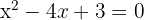


Buscamos el punto de corte con el eje 
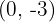
2
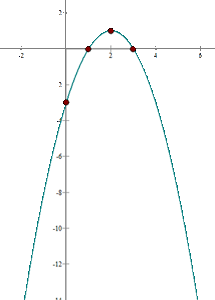
Calculamos las coordenadas del vértice


Buscamos los puntos de corte con el eje 

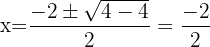
Coincide con el vértice: 
Buscamos el punto de corte con el eje 
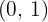
Calcula los siguientes valores de funciones cuadráticas
1Una función cuadrática tiene una expresión de la forma 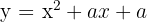 y pasa por el punto
y pasa por el punto  . Calcular el valor de
. Calcular el valor de  .
.
 y pasa por el punto
y pasa por el punto  . Calcular el valor de
. Calcular el valor de  .
. Sustituimos el punto en la función
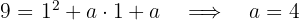
2Se sabe que la función cuadrática de ecuación 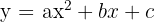 pasa por los puntos
pasa por los puntos 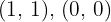 y
y  . Calcula
. Calcula  y
y  .
.
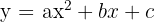 pasa por los puntos
pasa por los puntos 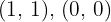 y
y  . Calcula
. Calcula  y
y  .
. Sustituimos el valor de cada punto en 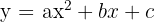
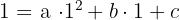
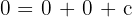
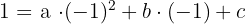
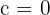
Resolvemos el sistema por reducción

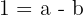


La función cuadrática es: 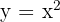
Si te animas con alguno de nuestros cursos de matematicas, no dudes en ponerte en contacto con nosotros.
3Considera las funciones cuadráticas 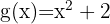 y
y  . Calcula sus puntos de intersección.
. Calcula sus puntos de intersección.
2Considera las funciones cuadráticas 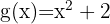 y
y  . Calcula sus puntos de intersección.
. Calcula sus puntos de intersección.
Para encontrar los puntos de intersección de estas funciones cuadráticas debemos igualar ambas funciones. Así se tiene que

Ahora, sustituimos estos valores de  en cualquiera de las funciones cuadráticas:
en cualquiera de las funciones cuadráticas:
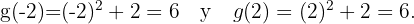
Por lo tanto, los puntos de intersección de las funciones cuadráticas son:





Apuntes es una plataforma dirigida al estudio y la práctica de las matemáticas a través de la teoría y ejercicios interactivos que ponemos a vuestra disposición. Esta información está disponible para todo aquel/aquella que quiera profundizar en el aprendizaje de esta ciencia. Será un placer ayudaros en caso de que tengáis dudas frente algún problema, sin embargo, no realizamos un ejercicio que nos presentéis de 0 sin que hayáis si quiera intentado resolverlo. Ánimo, todo esfuerzo tiene su recompensa.
Está mal la solución de la función inversa de f(x) = (2x+3)/x-1
Ya lo revise y no encuentro el error, podrías señalar en que está mal.
Determinar el límite de la función 𝑓(𝑥) =
9
(𝑥+1)
2
cuando la x tiende al infinito
Funcion exponencial
Porque no se puede representar analíticamente la función inversa de F(x) = 1 – 2/x²
F(x)=1-2x resuelvan o expliquenme xfis todos estos f(x)6-x.
F(x)x-2
F(x)3x-1 es para hoy xfis