Temas
Partimos de  que es la función de una parábola con vértice en el origen.
que es la función de una parábola con vértice en el origen.
Calculamos los valores por medio del método de tabulación.
 |  |
|---|---|
| -2 | 4 |
| -1 | 1 |
| 0 | 0 |
| 1 | 1 |
| 2 | 4 |
Y graficamos los valores, efectivamente tenemos una parábola con vértice en 


Definición de traslación
Es una transformación que consiste en desplazar cada uno de los puntos puntos de una figura en una misma dirección y la misma distancia, en este artículo nos centraremos en los diferentes casos en los que podemos trasladar una parábola.
Caso 1: Traslación vertical
Para hacer una transformación en vertical sumamos o restamos una constante, es decir,
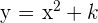
Si  ,
,  se desplaza hacia arriba
se desplaza hacia arriba  unidades
unidades
Si 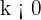 ,
,  se desplaza hacia abajo
se desplaza hacia abajo  unidades
unidades
El vértice de la parábola es: 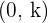
El eje de simetría 
Tomamos dos ejemplos donde la constante  es positiva y negativa.
es positiva y negativa.

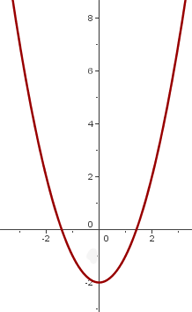
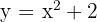
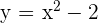
Caso 2: Traslación horizontal
Para hacer una transformación en horizontal sumamos o restamos una constante pero esta vez dentro del término cuadrático, es decir,

Si 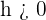 ,
,  se desplaza hacia la izquierda
se desplaza hacia la izquierda  unidades
unidades
Si 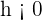 ,
,  se desplaza hacia la derecha
se desplaza hacia la derecha  unidades
unidades
El vértice de la parábola es: 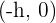
El eje de simetría es 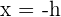
Tomamos dos ejemplos donde la constante  es positiva y negativa.
es positiva y negativa.
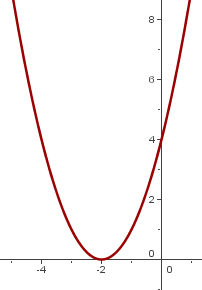
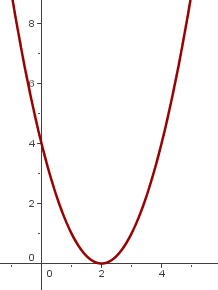
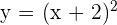

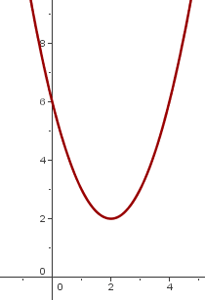
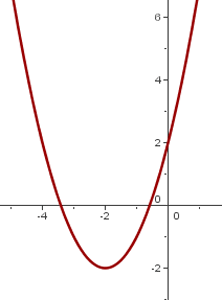
Caso 3: Traslación oblicua
La traslación oblicua es la combinación de una traslación vertical y horizontal, es decir,
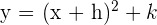
El vértice de la parábola es: 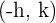
El eje de simetría es 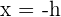
Tomamos dos ejemplos donde las constantes 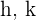 son positivas y negativas.
son positivas y negativas.
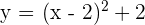
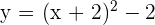













Apuntes es una plataforma dirigida al estudio y la práctica de las matemáticas a través de la teoría y ejercicios interactivos que ponemos a vuestra disposición. Esta información está disponible para todo aquel/aquella que quiera profundizar en el aprendizaje de esta ciencia. Será un placer ayudaros en caso de que tengáis dudas frente algún problema, sin embargo, no realizamos un ejercicio que nos presentéis de 0 sin que hayáis si quiera intentado resolverlo. Ánimo, todo esfuerzo tiene su recompensa.
Determinar el límite de la función 𝑓(𝑥) =
9
(𝑥+1)
2
cuando la x tiende al infinito
Funcion exponencial
Porque no se puede representar analíticamente la función inversa de F(x) = 1 – 2/x²
F(x)=1-2x resuelvan o expliquenme xfis todos estos f(x)6-x.
F(x)x-2
F(x)3x-1 es para hoy xfis
Un favor me podria ayudar este ejercicio?. Encontrar la funcion inversa f(x) = sen(x/2)
³√(x-3)/3