
Muestreo
1 En cierto barrio se quiere hacer un estudio para conocer mejor el tipo de actividades de ocio que gustan más a sus habitantes. Para ello van a ser encuestados 100 individuos elegidos al azar.
a Explicar qué procedimiento de selección sería más adecuado utilizar: muestreo con o sin reposición. ¿Por qué?
b Como los gustos cambian con la edad y se sabe que en el barrio viven 2.500 niños, 7.000 adultos y 500 ancianos, posteriormente se decide elegir la muestra anterior utilizando un muestreo estratificado con asignación proporcional. Determinar el tamaño muestral correspondiente a cada estrato.
a Como la población es finita, entonces hacer muestreo con reemplazo nos permitirá utilizar las fórmulas que hemos estudiado.
Sin embargo, es posible hacer muestreo sin reemplazo, con el único inconveniente que los cálculos serán un poco más complicados.
b Sea  el tamaño de la población y
el tamaño de la población y 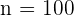 el tamaño de la muestra. Denotaremos como
el tamaño de la muestra. Denotaremos como 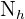 al tamaño del estrato
al tamaño del estrato  y
y  al tamaño de muestra que tomamos de
al tamaño de muestra que tomamos de  . En el muestreo estratificado con asignación proporcional se cumple que
. En el muestreo estratificado con asignación proporcional se cumple que
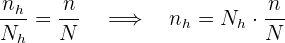
Por lo que debemos encontrar los valores  para cada estrato. Notemos que los tamaños de cada estrato
para cada estrato. Notemos que los tamaños de cada estrato 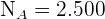 (niños),
(niños),  (adultos) y
(adultos) y 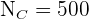 (ancianos).
(ancianos).
Así, el tamaño de muestra de niños es:

El tamaño de muestra de adultos es:

Por último, el tamaño de muestra de ancianos es:
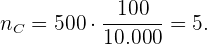
Observamos que los tamaños de muestra suman 100:
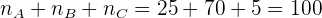
Intervalos de confianza
¿Buscas un profesor de algebra lineal? ¡Encuéntralo en Superprof!
2 Se ha tomado una muestra de los precios de un mismo producto alimenticio en 16 comercios, elegidos al azar en un barrio de una ciudad, y se han encontrado los siguientes precios:
95, 108, 97, 112, 99, 106, 105, 100, 99, 98, 104, 110, 107, 111, 103, 110.
Suponiendo que los precios de este producto siguen una distribución normal de varianza 25 y media desconocida:
a ¿Cuál es la distribución de la media muestral?
b Determine el intervalo de confianza, al 95%, para la media poblacional.
a Denotemos la media desconocida como  . Como los precios vienen de una distribución normal, entonces la media muestral también sigue una distribución muestral con media
. Como los precios vienen de una distribución normal, entonces la media muestral también sigue una distribución muestral con media  , y varianza
, y varianza 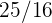 .
.
b Para determinar el intervalo de confianza, primero encontramos la media de la muestra:
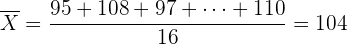
por lo que la fórmula es
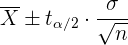
donde 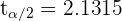 viene de una distribución t-Student con
viene de una distribución t-Student con 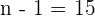 grados de libertad. Así, el intervalo de confianza es
grados de libertad. Así, el intervalo de confianza es

es decir,

3 La media de las estaturas de una muestra aleatoria de 400 personas de una ciudad es 1,75 m. Se sabe que la estatura de las personas de esa ciudad es una variable aleatoria que sigue una distribución normal con varianza 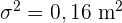 .
.
a Construye un intervalo, de un 95% de confianza, para la media de las estaturas de la población.
b ¿Cuál sería el mínimo tamaño muestral necesario para que pueda decirse que la verdadera media de las estaturas está a menos de 2 cm de la media muestral, con un nivel de confianza del 90%?
a Como la muestra consiste de 400 personas, entonces para calcular el intervalo de confianza, utilizamos la fórmula:
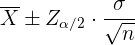
donde 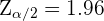 es el valor crítico de una distribución normal estándar.
es el valor crítico de una distribución normal estándar.
Además, 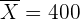 ,
,  y
y 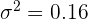 . De aquí se sigue que
. De aquí se sigue que 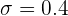 .
.
Así, el intervalo de confianza es
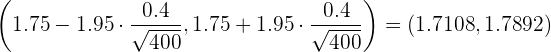
b Para encontrar el tamaño muestral utilizaremos  donde
donde 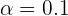 , por lo que
, por lo que  .
.

Así, al despejar  tenemos
tenemos
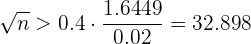
Por lo que  . Es decir, el tamaño de muestra debe ser al menos de
. Es decir, el tamaño de muestra debe ser al menos de 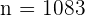 personas.
personas.
4 Las ventas mensuales de una tienda de electrodomésticos siguen una distribución normal, con desviación típica 900 €. En un estudio estadístico de las ventas realizadas en los últimos nueve meses, se ha encontrado un intervalo de confianza para la media mensual de las ventas, cuyos extremos son 4 663 € y 5 839 €.
a ¿Cuál ha sido la media de las ventas en estos nueve meses?
b ¿Cuál es el nivel de confianza para este intervalo?
¿Necesitas un profe mates?
a Cuando calculamos el intervalo de confianza de la media de una distribución normal, la media siempre se encontrará a la mitad del intervalo. Por lo tanto, la media es
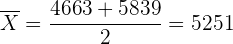
Esto es, la media fue de 5 251 €.
b Tenemos que  ,
,  y
y 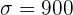 . De aquí se sigue que el límite inferior se calculó utilizando
. De aquí se sigue que el límite inferior se calculó utilizando
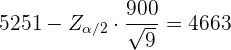
Es decir,

Por lo que

De aquí se sigue que 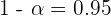 , por lo que el nivel de confianza fue de 95%.
, por lo que el nivel de confianza fue de 95%.
5 Se desea estimar la proporción  de individuos daltónicos de una población a través del porcentaje observado en una muestra aleatoria de individuos, de tamaño
de individuos daltónicos de una población a través del porcentaje observado en una muestra aleatoria de individuos, de tamaño  .
.
a Si el porcentaje de individuos daltónicos en la muestra es igual al 30%, calcula el valor de  para que, con un nivel de confianza de 0,95, el error cometido en la estimación sea inferior al 3,1%.
para que, con un nivel de confianza de 0,95, el error cometido en la estimación sea inferior al 3,1%.
b Si el tamaño de la muestra es de 64 individuos, y el porcentaje de individuos daltónicos en la muestra es del 35%, determina, usando un nivel de significación del 1%, el correspondiente intervalo de confianza para la proporción de daltónicos de la población.
a El intervalo de confianza para una proporción se calcula con la fórmula

como deseamos una confianza del 95%, entonces 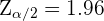 . Así, tenemos que
. Así, tenemos que

Despejando, tenemos que

Por lo que 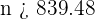 . Es decir, el tamaño de muestra debe ser de al menos 840 individuos.
. Es decir, el tamaño de muestra debe ser de al menos 840 individuos.
b Para encontrar el intervalo de confianza, simplemente reemplazamos en

los datos de 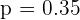 ,
,  . Notemos que
. Notemos que 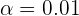 , por lo que
, por lo que  . Con esto, el intervalo de confianza es
. Con esto, el intervalo de confianza es
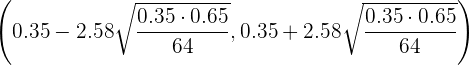
es decir,
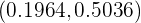
6 En una población una variable aleatoria sigue una distribución normal de media desconocida y desviación típica 2.
a Observada una muestra de tamaño 400, tomada al azar, se ha obtenido una media muestral igual a 50. Calcule un intervalo, con el 97% de confianza, para la media de la población.
b Con el mismo nivel de confianza, ¿qué tamaño mínimo debe tener la muestra para qué la amplitud del intervalo que se obtenga sea, como máximo, 1?
Tenemos que  ,
, 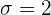 y
y  es desconocida.
es desconocida.
a Como 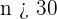 , entonces la distribución de la media se puede aproximar bien con una distribución normal. Por tanto, utilizamos la fórmula
, entonces la distribución de la media se puede aproximar bien con una distribución normal. Por tanto, utilizamos la fórmula
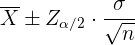
donde  . Así,
. Así, 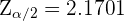 . Por lo tanto, el intervalo de confianza es
. Por lo tanto, el intervalo de confianza es
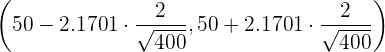
es decir,
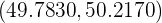
b Como se tiene el mismo nivel de confianza, entonces 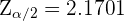 . Luego, para que la amplitud del intervalo sea 1, debemos tener que
. Luego, para que la amplitud del intervalo sea 1, debemos tener que
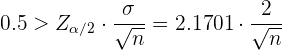
de donde despejaremos 

es decir 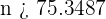 . Por lo tanto, el tamaño de muestra debe ser de al menos 76 individuos.
. Por lo tanto, el tamaño de muestra debe ser de al menos 76 individuos.
7 El tiempo que tardan las cajeras de un supermercado en cobrar a los clientes sigue una distribución normal con media desconocida y desviación típica 0,5 minutos. Para una muestra aleatoria de 25 clientes se obtuvo un tiempo medio de 5,2 minutos.
a Calcula el intervalo de confianza al nivel del 95% para el tiempo medio que se tarda en cobrar a los clientes.
b Indica el tamaño muestral necesario para estimar dicho tiempo medio con un el error de 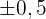 minutos y un nivel de confianza del 95%.
minutos y un nivel de confianza del 95%.
a Como la muestra consiste de 25 clientes, entonces para calcular el intervalo de confianza, utilizamos la fórmula:
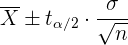
donde 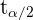 es el valor crítico tal que
es el valor crítico tal que  donde
donde  es una variable aleatoria que sigue una distribución t-Student con 24 grados de libertad.
es una variable aleatoria que sigue una distribución t-Student con 24 grados de libertad.
El valor de 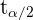 lo podemos obtener de una tabla de distribución t, o utilizando un software. El resultado es
lo podemos obtener de una tabla de distribución t, o utilizando un software. El resultado es 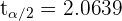
Así, el intervalo de confianza es
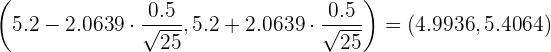
b Para encontrar el tamaño muestral reemplazaremos 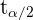 por
por  , el cual proviene de una distribución normal estándar. Como el error debe ser
, el cual proviene de una distribución normal estándar. Como el error debe ser  , entonces se debe tener
, entonces se debe tener

donde 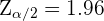 . Así, al despejar
. Así, al despejar  tenemos
tenemos
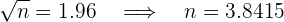
es decir, el tamaño de muestra debe ser al menos de  .
.
8 La cantidad de hemoglobina en sangre del hombre sigue una distribución normal con una desviación típica de 2 g/dl.
Se obtuvo de una muestra de 12 extracciones y se calculó el intervalo de confianza para la media poblacional de la hemoglobina en la sangre. Si el intervalo obtenido fue entre 13 y 15 g/dl, ¿cuál es el nivel de confianza de este intervalo?
En este ejercicio ya conocemos el intervalo de confianza y lo que se nos pide calcular es el nivel de confianza, es decir,  .
.
Notemos que tenemos que 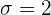 ,
, 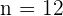 y
y
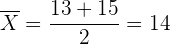
es decir, la media es el punto medio del intervalo.
Como la muestra proviene de una población que sigue distribución normal, entonces el límite inferior del intervalo se calcula utilizando
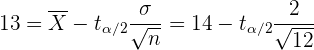
ya que el tamaño de muestra  . Además,
. Además, 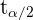 es el valor crítico de una distribución t-Student con 11 grados de libertad. Así, despejando
es el valor crítico de una distribución t-Student con 11 grados de libertad. Así, despejando 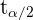 obtenemos
obtenemos

Por tanto, tenemos que 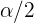 se calcula utilizando
se calcula utilizando

Así,  y
y  . Es decir, el intervalo tiene una confiabilidad del 88.85%.
. Es decir, el intervalo tiene una confiabilidad del 88.85%.
Pruebas de hipótesis con intervalos de confianza
Si quieres encontrar un profesor en linea algebra, ¿por qué no pruebas en Superprof?
9 Una marca de nueces afirma que, como máximo, el 6% de las nueces están vacías. Se eligieron 300 nueces al azar y se detectaron 21 vacías.
a Con un nivel de significación del 1%, ¿se puede aceptar la afirmación de la marca?
b Si se mantiene el porcentaje muestral de nueces que están vacías y 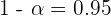 , ¿qué tamaño muestral se necesitaría para estimar la proporción de nueces con un error menor del 1%?
, ¿qué tamaño muestral se necesitaría para estimar la proporción de nueces con un error menor del 1%?
a El primer inciso involucra una prueba de hipótesis donde deseamos verificar que cierta proporción es menor a un valor dador. Así, la hipótesis nula es

mientras que la hipótesis alternativa es
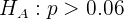
donde 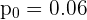 es la proporción hipotética.
es la proporción hipotética.
El límite superior del intervalo de confianza para la proporción se calcula utilizando
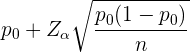
ya que se trata de un contraste unilateral. Para este caso, tenemos que 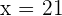 ,
, 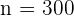 y
y 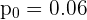 . Para nuestra significancia de
. Para nuestra significancia de 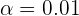 , el valor crítico que le corresponde es
, el valor crítico que le corresponde es  . Así, el intervalo de confianza es
. Así, el intervalo de confianza es
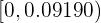
Dado que 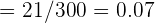 sí está dentro del intervalo de confianza, entonces aceptamos la hipótesis nula.
sí está dentro del intervalo de confianza, entonces aceptamos la hipótesis nula.
En consecuencia, concluimos que, el 6% de las nueces están vacías como máximo. Es decir, no tenemos evidencia suficiente para garantizar lo contrario.
b El porcentaje muestral de nueces vacías es del 7%. Por tanto, la proporción es 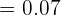 . Sabemos que el error de estimación es
. Sabemos que el error de estimación es
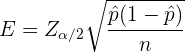
que en este caso deseamos que sea menor a 0.01. Además, para  el valor crítico asociado es
el valor crítico asociado es 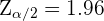 .
.
De este modo, tenemos que,
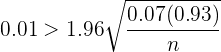
que al despejar  , obtenemos
, obtenemos
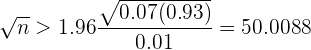
Así, tenemos que

De este modo, el tamaño de población debe ser mayor o igual a 2501.
10 La duración de la bombillas de 100 W que fabrica una empresa sigue una distribución normal con una desviación típica de 120 horas de duración. Su vida media está garantizada durante un mínimo de 800 horas. Se escoge al azar una muestra de 50 bombillas de un lote y, después de comprobarlas, se obtiene una vida media de 750 horas. Con un nivel de significación de 0,01, ¿habría que rechazar el lote por no cumplir la garantía?
Este problema trata de una prueba de hipótesis donde deseamos verificar si la vida media es, por lo menos, un valor dado (800 horas). Por tanto, se trata de un contraste unilateral y la hipótesis nula es

y la hipótesis alternativa es

donde la media hipotética es  .
.
Al tratarse de una hipótesis sobre la media, entonces el intervalo de confianza unilateral es
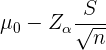
y en este caso tenemos que 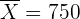 ,
, 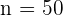 ,
,  y
y 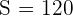 . Además, a la significancia de
. Además, a la significancia de 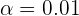 le corresponde un valor crítico de
le corresponde un valor crítico de  . Luego, el intervalo de confianza es
. Luego, el intervalo de confianza es

es decir, 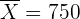 no está dentro del intervalo de confianza, por lo que podemos rechazar la hipótesis nula.
no está dentro del intervalo de confianza, por lo que podemos rechazar la hipótesis nula.
Esto es, se concluye que tenemos evidencia suficiente para rechazar la hipótesis nula. Por lo tanto, la vida media es menor a 800 horas y podemos rechazar el lote ya que no se cumple la garantía.
11 Se sabe que la desviación típica de las notas de cierto examen de Matemáticas es 2,4. Para una muestra de 36 estudiantes se obtuvo una nota media de 5,6. ¿Sirven estos datos para confirmar la hipótesis de que la nota media del examen fue de 6, con un nivel de confianza del 95%?
Notemos que se trata de una prueba de hipótesis para el valor promedio en la calificación del examen. Es decir, la hipótesis nula es
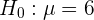
mientras que la hipótesis alternativa es

donde 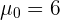 . Como queremos probar que el promedio es igual a cierto valor, entonces utilizaremos un contraste bilateral.
. Como queremos probar que el promedio es igual a cierto valor, entonces utilizaremos un contraste bilateral.
Si asumimos que las notas siguen aproximadamente una distribución normal, entonces el intervalo de confianza para  es
es
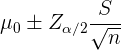
Además, en este caso tenemos que 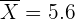 ,
,  y
y 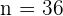 . Como el nivel de confianza es 95% y el contraste es bilateral, entonces
. Como el nivel de confianza es 95% y el contraste es bilateral, entonces 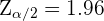 . Sin embargo, tenemos que el intervalo de confianza es
. Sin embargo, tenemos que el intervalo de confianza es
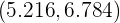
Por tanto, aceptamos la hipótesis nula ya que 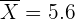 está dentro del intervalo de confianza. Es decir, aceptamos que la nota media es de 6.
está dentro del intervalo de confianza. Es decir, aceptamos que la nota media es de 6.
Recordemos que esto sólo significa que no tenemos evidencia suficiente para decir que la nota sea diferente a 6.













Apuntes es una plataforma dirigida al estudio y la práctica de las matemáticas a través de la teoría y ejercicios interactivos que ponemos a vuestra disposición. Esta información está disponible para todo aquel/aquella que quiera profundizar en el aprendizaje de esta ciencia. Será un placer ayudaros en caso de que tengáis dudas frente algún problema, sin embargo, no realizamos un ejercicio que nos presentéis de 0 sin que hayáis si quiera intentado resolverlo. Ánimo, todo esfuerzo tiene su recompensa.
En la siguiente tabla se presentan las cantidades promedio de jugo de frutas que empacan, en bolsas de litro, tres máquinas empacadas de una agroindustria.
-MAQUINAS
A
B
C
-PROMEDIO EMPACADO POR BOLSA
1.039 LTS
0.989 LTS
1.090 LTS
-DESVIACIÓN ESTANDAR
0.332 LTS
0.350 LTS
0.371 LTS
¿Cuál de las 3 máquinas tiene la cantidad promedio de empacado por bolsa más confiable? ¿Por qué?
ejercicio. En una ciudad de 100.000 habitantes, se quiere estimar la proporción de personas que utilizan bicicleta como medio de transporte. ¿Cuántas personas deben incluirse en la muestra para obtener un margen de error del 5% con un nivel de confianza del 95%?
10.- Las estaturas de cierta población se distribuyen N(168,8). Calcula la probabilidad de que en una muestra de 36 personas la altura media no difiera de la de la población en más de 1 cm.
28 28 28 28 24 24 20 20 20 20 20 25 25 25 27 27 27 26 22 22 22
En una escuela de 150 estudiantes se requiere realizar una investigación sobre las preferencias de las áreas de los estudiantes y se debe calcular su muestra para conocer cuántos estudiantes se le debe aplicar la encuesta, determinando que el grado de confianza es del 95%, la probabilidad de éxito de 98% y el error de calculo del 6%.
Caso de estudio: En el Perú, el Ministerio de Salud (MINSA) está interesado en conocer la prevalencia de la depresión en los adolescentes de 12 a 17 años de edad en la ciudad de Lima. Para ello, el MINSA decide realizar una encuesta a una muestra de adolescentes de esta población.
Objetivo:
El objetivo del caso de estudio es que los estudiantes apliquen la fórmula para estimar una proporción poblacional para estimar la prevalencia de la depresión en los adolescentes de 12 a 17 años de edad en la ciudad de Lima. También, debe indicar el tipo de muestreo probabilístico que deberá emplear.
¿Cuál debe ser el tamaño de muestra para estimar la prevalencia de la depresión, con un nivel de confianza del 95%, margen de error de 4%, e indica el método de selección de la muestra
La experiencia con los trabajado indica que el tiempo requerido para que un trabajador cualquiera termine un trabajo, es una variable con distribución aproximada a la normal con una media de 145 minutos y una desviación estándar de 12 minutos. Se lleva a cabo un programa de capacitación con el propósito de mejorar la destreza de los trabajadores y disminuir así el tiempo medio. Para verificar los resultados de dicho programa se toma al azar una muestra de 16 trabajadores y si esta muestra arroja un tiempo medio mayor que 139 minutos se aceptará la hipótesis de que el tiempo medio sigue siendo de 145 minutos. Pruebe la hipótesis con un nivel de significancia del 5%.
Una empresa de seguros ha estado aplicando diferentes técnicas para incrementar sus ventas durante los últi mos 6 meses. El promedio de ventas por semestre es de 54 ventas diarias, con una muestra aleatoria de 60 días de los últimos 6 meses, se obtiene que en promedio hay 60 ventas diarias con una desviación estándar de 28 Con un nivel de significación de 5%, es posible asegu rar que el promedio de ventas aumento?
A una muestra aleatoria de 150 alumnos de la universidad, se le preguntó si había estudiado el idioma inglés. 75 respondieron Sí, 55 respondieron No y 20 no opinaron. a. ¿Cuál es el valor de la estimación puntual de la proporción de la población que responde Sí?. b. ¿Cuál es el valor de la estimación puntual de la proporción de la población que respondió No?. c. Encuentre el intervalo de confianza del 90% para la proporción poblacional que respondieron Sí. Fuente de ingresos Frecuencia Propina sólo domingos 149 Quehaceres, dádivas y domingos 219 Quehaceres y dádivas, no domingos 251 Nada 165 T o t a l 784
Se quiere hacer un estudio para conocer el número de mujeres casadas que van a consulta ginecológicas en una población, por estudios anteriores se sabe que la desviación estándar de 1 mujeres, el investigador considera que el margen de error es de 9% y el coeficiente de confianza es de 91%.