Temas
- Indica cuáles variables son cualitativas y cuáles cuantitativas
- De las siguientes variables indica cuáles son discretas y cuales continuas
- Clasificar las siguientes variables en cualitativas o cuantitativas, y en discretas o continuas
- Ejercicios sobre construcción de tabla de distribución de frecuencias
- Ejercicios de tabla de frecuencias, histograma y polígonos de frecuencias
- Ejercicios sobre medidas de tendencia central

Indica cuáles variables son cualitativas y cuáles cuantitativas
Opta por las clases particulares matematicas madrid que te ofrecemos en Superprof para conseguir tus mejores resultados y alcanzar tus objetivos.
Para ello, te damos unas breves pautas de ejemplos de variables cualitativas y cuantitativas:
1 Comida Favorita.
2 Profesión que te gusta.
3 Número de goles marcados por tu equipo favorito en la última temporada.
4 Número de alumnos de tu Instituto.
5 El color de los ojos de tus compañeros de clase.
6 Coeficiente intelectual de tus compañeros de clase.
Indica cuáles variables son cualitativas y cuales cuantitativas:
1 Comida Favorita.
Cualitativa
2 Profesión que te gusta.
Cualitativa
3 Número de goles marcados por tu equipo favorito en la última temporada.
Cuantitativa
4 Número de alumnos de tu Instituto.
Cuantitativa
5 El color de los ojos de tus compañeros de clase.
Cualitativa
6 Coeficiente intelectual de tus compañeros de clase.
Cuantitativa
De las siguientes variables indica cuáles son discretas y cuales continuas
1 Número de acciones vendidas cada día en la Bolsa.
2 Temperaturas registradas cada hora en un observatorio.
3 Período de duración de un automóvil.
4 El diámetro de las ruedas de varios coches.
5 Número de hijos de  familias.
familias.
6 Censo anual de los españoles.
De las siguientes variables indica cuáles son discretas y cuales continuas.
1 Número de acciones vendidas cada día en la Bolsa.
Discreta
2 Temperaturas registradas cada hora en un observatorio.
Continua
3 Período de duración de un automóvil.
Continua
4 El diámetro de las ruedas de varios coches.
Continua
5 Número de hijos de  familias.
familias.
Discreta
6 Censo anual de los españoles.
Discreta
Clasificar las siguientes variables en cualitativas o cuantitativas, y en discretas o continuas
1 La nacionalidad de una persona.
2 Número de litros de agua contenidos en un depósito.
3 Número de libros en un estante de librería.
4 Suma de puntos tenidos en el lanzamiento de un par de dados.
5 La profesión de una persona.
6 El área de las distintas baldosas de un edificio.
Clasificar las siguientes variables en cualitativas o cuantitativas, y en discretas o continuas.
1 La nacionalidad de una persona.
Cualitativa
2 Número de litros de agua contenidos en un depósito.
Cuantitativa y continua
3 Número de libro en un estante de librería.
Cuantitativa y discreta
4 Suma de puntos tenidos en el lanzamiento de un par de dados.
Cuantitativa y discreta
5 La profesión de una persona.
Cualitativa
6 El área de las distintas baldosas de un edificio.
Cuantitativa y continua
Ejercicios sobre construcción de tabla de distribución de frecuencias
1 Las puntuaciones obtenidas por un grupo en una prueba han sido:

Construir la tabla de distribución de frecuencias y dibujar el polígono de frecuencias.
Las puntuaciones obtenidas por un grupo en una prueba han sido:

Construir la tabla de distribución de frecuencias y dibuja el
polígono de frecuencias.
 | Recuento |  |  |  |  |
 |  |  |  |  |  |
 |  |  |  |  |  |
 |  |  |  |  | 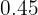 |
 |  |  |  |  |  |
 |  |  |  |  |  |
 |  |  |  |  |  |
 | 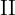 |  |  |  |  |
 |  |  |  |  |  |
 |
-
- En la cuarta columna disponemos la frecuencia acumulada
 .
.
- En la cuarta columna disponemos la frecuencia acumulada
-
- En la primera casilla colocamos la primera frecuencia absoluta.
-
- En la segunda casilla sumamos el valor de la frecuencia acumulada anterior más la frecuencia absoluta correspondiente y así sucesivamente hasta la última, que tiene que ser igual a
 .
.
- En la segunda casilla sumamos el valor de la frecuencia acumulada anterior más la frecuencia absoluta correspondiente y así sucesivamente hasta la última, que tiene que ser igual a
-
- En la quinta columna disponemos las frecuencias relativas,
 , que
, que
son el resultado de dividir cada frecuencia absoluta por .
.
- En la quinta columna disponemos las frecuencias relativas,
-
- En la sexta columna disponemos la frecuencia relativa acumulada
 .
.
- En la sexta columna disponemos la frecuencia relativa acumulada
-
- En la primera casilla colocamos la primera frecuencia relativa.
- En la segunda casilla sumamos el valor de la frecuencia relativa acumulada anterior más la frecuencia relativa acumulada correspondiente y así sucesivamente hasta la última, que tiene que ser igual a
 .
.
Polígono de frecuencias
En eje de abscisas van los datos y en el de ordenadas las frecuencias absolutas

2 El número de estrellas de los hoteles de una ciudad viene dado por la siguiente serie:

Construir la tabla de distribución de frecuencias y dibuja el diagrama de barras.
El número de estrellas de los hoteles de una ciudad viene dado por la siguiente serie:

Pasos para construir la tabla de distribución de frecuencias y dibujar el diagrama de barras.
 | Recuento |  |  |  |  |
 |  |  |  |  |  |
 |  |  |  |  |  |
 |  |  |  |  |  |
 |  |  |  |  |  |
 |  |
-
- En la cuarta columna disponemos la frecuencia acumulada
 .
.
- En la cuarta columna disponemos la frecuencia acumulada
-
- En la primera casilla colocamos la primera frecuencia absoluta.
-
- En la segunda casilla sumamos el valor de la frecuencia acumulada anterior más la frecuencia absoluta correspondiente y así sucesivamente hasta la última, que tiene que se igual a
 .
.
- En la segunda casilla sumamos el valor de la frecuencia acumulada anterior más la frecuencia absoluta correspondiente y así sucesivamente hasta la última, que tiene que se igual a
-
- En la quinta columna disponemos las frecuencias relativas (
 ) que
) que
son el resultado de dividir cada frecuencia absoluta por .
.
- En la quinta columna disponemos las frecuencias relativas (
-
- En la sexta columna disponemos la frecuencia relativa acumulada
 .
.
- En la sexta columna disponemos la frecuencia relativa acumulada
-
- En la primera casilla colocamos la primera frecuencia relativa.
- En la segunda casilla sumamos el valor de la frecuencia relativa acumulada anterior más la frecuencia relativa acumulada correspondiente y así sucesivamente hasta la última, que tiene que ser igual a
 .
.
Diagrama de barras
En eje de abscisas van los datos y en el de ordenadas las frecuencias absolutas.

3 Las calificaciones de  alumnos han sido las siguientes:
alumnos han sido las siguientes:

Construir la tabla de distribución de frecuencias y dibuja el diagrama de barras.
Las calificaciones de  alumnos han sido las siguientes:
alumnos han sido las siguientes:

Pasos para construir la tabla de distribución de frecuencias y dibujar el
diagrama de barras.
 |  |  |  |  |
 |  |  |  |  |
 1 1 |  |  |  |  |
 |  |  |  |  |
 |  |  |  |  |
 |  |  |  |  |
 |  |  |  |  |
 |  |  |  |  |
 |  |  |  |  |
 |  |  |  |  |
 |  |  |  |  |
 |  |  |  |  |
 |  |
-
- En la cuarta columna disponemos la frecuencia acumulada
 .
.
- En la cuarta columna disponemos la frecuencia acumulada
-
- En la primera casilla colocamos la primera frecuencia absoluta.
-
- En la segunda casilla sumamos el valor de la frecuencia acumulada anterior más la frecuencia absoluta correspondiente y así sucesivamente hasta la última, que tiene que se igual a
 .
.
- En la segunda casilla sumamos el valor de la frecuencia acumulada anterior más la frecuencia absoluta correspondiente y así sucesivamente hasta la última, que tiene que se igual a
-
- En la quinta columna disponemos las frecuencias relativas (
 ) que son el resultado de dividir cada frecuencia absoluta por
) que son el resultado de dividir cada frecuencia absoluta por  .
.
- En la quinta columna disponemos las frecuencias relativas (
-
- En la sexta columna disponemos la frecuencia relativa acumulada
 .
.
- En la sexta columna disponemos la frecuencia relativa acumulada
-
- En la primera casilla colocamos la primera frecuencia relativa.
- En la segunda casilla sumamos el valor de la frecuencia relativa acumulada anterior más la frecuencia relativa acumulada correspondiente y así sucesivamente hasta la última, que tiene que ser igual a

Diagrama de barras
En eje de abscisas van los datos y en el de ordenadas las frecuencias absolutas.

Ejercicios de tabla de frecuencias, histograma y polígonos de frecuencias
1 Los pesos de los  empleados de una fábrica vienen dados por la siguiente tabla:
empleados de una fábrica vienen dados por la siguiente tabla:
| Peso |  |
 |  |
 |  |
 |  |
 |  |
 |  |
 |  |
 |  |
a) Construir la tabla de frecuencias.
b) Representar el histograma y el polígono de frecuencias.
Los pesos de los  empleados de una fábrica vienen dados por la siguiente tabla:
empleados de una fábrica vienen dados por la siguiente tabla:
| Peso |  |
 |  |
 |  |
 |  |
 |  |
 |  |
 |  |
 |  |
a) Construir la tabla de frecuencias.
 |  |  |  |  | |
 |  |  |  |  |  |
 |  |  |  |  | 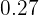 |
 |  |  |  |  |  |
 |  |  |  |  |  |
 |  |  |  |  |  |
 |  |  |  |  |  |
 |  |  |  |  |  |
 |
-
- En la cuarta columna disponemos la frecuencia acumulada
 .
.
- En la cuarta columna disponemos la frecuencia acumulada
-
- En la primera casilla colocamos la primera frecuencia absoluta.
-
- En la segunda casilla sumamos el valor de la frecuencia acumulada anterior más la frecuencia absoluta correspondiente y así sucesivamente hasta la última, que tiene que se igual a
 .
.
- En la segunda casilla sumamos el valor de la frecuencia acumulada anterior más la frecuencia absoluta correspondiente y así sucesivamente hasta la última, que tiene que se igual a
-
- En la quinta columna disponemos las frecuencias relativas (
 ) que son el resultado de dividir cada frecuencia absoluta por
) que son el resultado de dividir cada frecuencia absoluta por  .
.
- En la quinta columna disponemos las frecuencias relativas (
-
- En la sexta columna disponemos la frecuencia relativa acumulada
 .
.
- En la sexta columna disponemos la frecuencia relativa acumulada
-
- En la primera casilla colocamos la primera frecuencia relativa.
- En la segunda casilla sumamos el valor de la frecuencia relativa acumulada anterior más la frecuencia relativa acumulada correspondiente y así sucesivamente hasta la última, que tiene que ser igual a
 .
.
b) Representar el histograma y el polígono de frecuencias.
Histograma
El polígono de frecuencias lo construimos uniendo los puntos medios de cada rectángulo

2Los  alumnos de una clase han obtenido las siguientes puntuaciones sobre
alumnos de una clase han obtenido las siguientes puntuaciones sobre  , en un examen de Física.
, en un examen de Física.

a)Construir la tabla de frecuencias.
b) Dibujar el histograma y el polígono de frecuencias
Los  alumnos de una clase han obtenido las siguientes puntuaciones sobre
alumnos de una clase han obtenido las siguientes puntuaciones sobre  , en un examen de Física.
, en un examen de Física.

a) Construir la tabla de frecuencias.
 |  |  |  |  | |
 |  |  |  |  |  |
 |  |  |  |  | 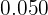 |
 |  |  |  |  |  |
 |  |  |  |  |  |
 |  |  |  |  |  |
 |  |  |  |  |  |
 |  |  |  |  |  |
 |  |  |  |  |  |
 |  |  |  |  | 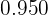 |
 |  |  |  | 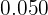 |  |
 |  |
-
- En la cuarta columna disponemos la frecuencia acumulada
 .
.
- En la cuarta columna disponemos la frecuencia acumulada
-
- En la primera casilla colocamos la primera frecuencia absoluta.
-
- En la segunda casilla sumamos el valor de la frecuencia acumulada anterior más la frecuencia absoluta correspondiente y así sucesivamente hasta la última, que tiene que se igual a
 .
.
- En la segunda casilla sumamos el valor de la frecuencia acumulada anterior más la frecuencia absoluta correspondiente y así sucesivamente hasta la última, que tiene que se igual a
-
- En la quinta columna disponemos las frecuencias relativas (
 ) que son el resultado de dividir cada frecuencia absoluta por
) que son el resultado de dividir cada frecuencia absoluta por  .
.
- En la quinta columna disponemos las frecuencias relativas (
-
- En la sexta columna disponemos la frecuencia relativa acumulada
 .
.
- En la sexta columna disponemos la frecuencia relativa acumulada
-
- En la primera casilla colocamos la primera frecuencia relativa.
- En la segunda casilla sumamos el valor de la frecuencia relativa acumulada anterior más la frecuencia relativa acumulada correspondiente y así sucesivamente hasta la última, que tiene que ser igual a
 .
.
b) Dibujar el histograma y el polígono de frecuencias.
Histograma
El polígono de frecuencias lo construimos uniendo los puntos medios de cada rectángulo

Ejercicios sobre medidas de tendencia central
1 Sea una distribución estadística que viene dada por la siguiente tabla:
 |  |
 |  |
 |  |
 |  |
 |  |
 |  |
Calcular:
a) La moda, mediana y media.
b) El rango, desviación media, varianza y desviación típica.
Sea una distribución estadística que viene dada por la siguiente tabla:
 |  |
 |  |
 |  |
 |  |
 |  |
 |  |
Calcular:
a) La moda, mediana y media.
b) El rango, desviación media, varianza y desviación típica.
Completamos la tabla con:
-
- La frecuencia acumulada (
 ) para calcular la mediana
) para calcular la mediana
- La frecuencia acumulada (
-
- El producto de la variable por su frecuencia absoluta (
 ) para calcular la media
) para calcular la media
- El producto de la variable por su frecuencia absoluta (
-
- La desviación respecto a la media
 y su producto por la frecuencia absoluta
y su producto por la frecuencia absoluta  para calcular la desviación media
para calcular la desviación media
- La desviación respecto a la media
- El producto de la variable al cuadrado por su frecuencia absoluta (
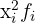 ) para calcular la varianza y la desviación típica
) para calcular la varianza y la desviación típica
 |  |  |  |  |  | 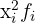 |
 |  |  |  |  |  |  |
 |  |  |  |  |  | 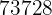 |
 |  |  |  | 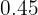 |  |  |
 |  |  |  |  |  |  |
 |  |  |  |  |  |  |
 |  |  |  |
Moda
La moda es el valor que tiene mayor frecuencia absoluta.
Miramos en la columna de las  y la frecuencia absoluta mayor,
y la frecuencia absoluta mayor,  ,corresponde a
,corresponde a  .
.
 .
.
Mediana
Para calcular la mediana dividimos  entre
entre  y vemos que la casilla de las
y vemos que la casilla de las  donde se encuentra que la
donde se encuentra que la  mas cercana a
mas cercana a  es
es  y corresponde a
y corresponde a  .
.


Media
Calculamos la sumatoria de la variable por su frecuencia absoluta ( ) que es
) que es  y la dividimos por
y la dividimos por  .
.

Desviación media
Calculamos la sumatoria de de los productos de desviaciones respecto a la media por sus frecuencias absolutas correspondientes  que es
que es  y dividimos por
y dividimos por  .
.

Rango
Realizamos la la diferencia entre el mayor y el menor de los valores
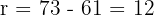 .
.
Varianza
Calculamos la sumatoria de  , la dividimos por
, la dividimos por  y al resultado le restaremos la media aritmética al cuadrado
y al resultado le restaremos la media aritmética al cuadrado 
 .
.
Desviación típica
Hacemos la raíz cuadrada de la varianza

2 Calcular la media, la mediana y la moda de la siguiente serie de números:

Calcular la media, la mediana y la moda de la siguiente serie de números:

Creamos una tabla con las siguientes columnas:
-
- Los valores de la variable (
 ).
).
- Los valores de la variable (
-
- Las frecuencias absolutas (
 ).
).
- Las frecuencias absolutas (
-
- Las frecuencias acumuladas (
 ) para calcular la mediana.
) para calcular la mediana.
- Las frecuencias acumuladas (
- El producto de la variable por su frecuencia absoluta (
 ) para calcular la media.
) para calcular la media.
 |  |  |  |
 |  |  |  |
 |  |  |  |
 |  |  |  |
 |  |  |  |
 |  |  |  |
 |  |  |  |
 |  |
Moda
La moda es el valor que tiene mayor frecuencia absoluta.
Miramos en la columna de las  y la frecuencia absoluta mayor,
y la frecuencia absoluta mayor,  , corresponde a
, corresponde a  .
.
 .
.
Mediana
Para calcular la mediana dividimos  entre
entre  y vemos que la casilla de las
y vemos que la casilla de las  donde se encuentra
donde se encuentra  corresponde a
corresponde a  .
.
 .
.
Media
Calculamos la sumatoria de la variable por su frecuencia absoluta ( ) que es
) que es  y la dividimos por
y la dividimos por  .
.
 .
.
3 Hallar la varianza y la desviación típica de la siguiente serie de datos:

Hallar la varianza y la desviación típica de la siguiente serie de datos:

Calculamos la media aritmética:
 .
.
Aplicamos la fórmula de la varianza:
 .
.
Realizamos la raíz cuadrada de la varianza:
 .
.
4 Hallar la media, mediana y moda de la siguiente serie de números:

Hallar la media, mediana y moda de la siguiente serie de números:

Moda
La moda es  porque es el valor que más se repite.
porque es el valor que más se repite.
 .
.
Mediana
La serie tiene un número par de puntuaciones, la mediana será la media entre las dos puntuaciones centrales.
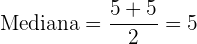 .
.
Media
Aplicamos la fórmula de la media.
 .
.
5Hallar la desviación media, la varianza y la desviación típica de la series de números siguientes:
1 
2 
Hallar la desviación media, la varianza y la desviación típica de la series de números siguientes:
1 
Media

Desviación media

Varianza
 .
.
Desviación típica
 .
.
2 
Media
 .
.
Desviación media
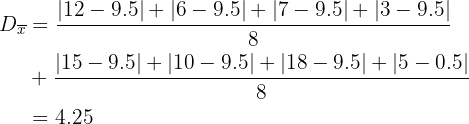 .
.
Varianza

Desviación típica
 .
.
6Se ha aplicado un test a los empleados de una fábrica, obteniéndose la siguiente tabla:
 | |
 |  |
 |  |
 |  |
 |  |
 |  |
 |  |
 |  |
Dibujar el histograma y el polígono de frecuencias acumuladas.
Se ha aplicado un test a los empleados de una fábrica, obteniéndose las siguiente tabla:
 | |
 |  |
 |  |
 |  |
 |  |
 |  |
 |  |
 |  |
Dibujar el histograma y el polígono de frecuencias acumuladas.
Agregamos una nueva columna donde disponemos las frecuencias acumuladas ( ):
):
En la primera casilla colocamos la primera frecuencia absoluta.
En la segunda casilla sumamos el valor de la frecuencia acumulada anterior más la frecuencia absoluta correspondiente y así sucesivamente hasta la última, que tiene que ser igual a  .
.
 |  | |
 |  |  |
 |  |  |
 |  |  |
 |  |  |
 |  |  |
 |  |  |
 |  |  |
 |

¿Necesitas clases particulares matematicas? ¡En Superprof te encontramos al profesor que mejor se adapte a lo que buscas!
7Dadas las series estadísticas:
a) 
b) 
Calcular
-
- La moda, la mediana y la media.
-
- La desviación media, la varianza y la desviación típica.
-
- Los cuartiles
 y
y  .
.
- Los cuartiles
-
- Los deciles
 y
y  .
.
- Los deciles
- Los percentiles
 y
y  .
.
Dadas las series estadísticas:
a) 
b) 
Calcular
-
- La moda, la mediana y la media.
-
- La desviación media, la varianza y la desviación típica.
-
- Los cuartiles
 y
y  .
.
- Los cuartiles
-
- Los deciles
 y
y  .
.
- Los deciles
- Los percentiles
 y
y  .
.
a) 
Moda
No existe moda porque todas las puntuaciones tienen la misma frecuencia.
Mediana
Ordenando los datos tenemos:

Por lo tanto la mediana es
 .
.
Media

Varianza

Desviación típica

Desviación media

Rango

Cuartiles

Deciles
Tenemos que la fórmula para la posición de los deciles está dada por

Por lo tanto, los deciles que buscamos están en las posiciones:

Percentiles
Tenemos que la fórmula para la posición de los percentiles está dada por

Por lo tanto, los percentiles que buscamos están en las posiciones:

b) 
Moda
No existe moda porque todas las puntuaciones tienen la misma frecuencia.
Mediana
Ordenando los datos tenemos:

Por lo tanto la mediana es
 .
.
Media

Varianza

Desviación típica

Desviación media

Rango

Cuartiles

Deciles
Tenemos que la fórmula para la posición de los deciles está dada por

Por lo tanto, los deciles que buscamos están en las posiciones:

Percentiles
Tenemos que la fórmula para la posición de los percentiles está dada por

Por lo tanto, los percentiles que buscamos están en las posiciones:

8 Una distribución estadística viene dada por la siguiente tabla:
 | |
 |  |
 |  |
 |  |
 |  |
 |  |
Hallar:
a) La moda, mediana y media.
b) El rango, desviación media y varianza.
c) Los cuartiles  y
y  .
.
d) Los deciles  y
y  .
.
e) Los percentiles  y
y  .
.
Una distribución estadística viene dada por la siguiente tabla:
 | |
 |  |
 |  |
 |  |
 |  |
 |  |
Hallar:
a) La moda, mediana y media.
b) El rango, desviación media y varianza.
c) Los cuartiles  y
y  .
.
d) Los deciles  y
y  .
.
e) Los percentiles  y
y  .
.
Completamos la tabla con:
La frecuencia acumulada ( ) para calcular la mediana.
) para calcular la mediana.
El producto de la variable por su frecuencia absoluta ( ) para calcular la media.
) para calcular la media.
La desviación respecto a la media  y su producto por la frecuencia absoluta
y su producto por la frecuencia absoluta  para calcular la desviación media
para calcular la desviación media
El producto de la variable al cuadrado por su frecuencia absoluta (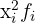 ) para calcular la varianza y la desviación típica
) para calcular la varianza y la desviación típica
 |  |  |  |  | 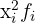 | |
 |  |  |  |  |  |  |
 |  |  |  |  |  |  |
 |  |  |  |  |  |  |
 |  |  |  |  |  |  |
 |  |  |  |  |  |  |
 |  |  |  |
Moda
En primer lugar buscamos el intervalo donde se encuentra la moda, que será el intervalo que tenga la mayor frecuencia absoluta ( )
)
La clase modal es: 
Aplicaremos la fórmula para el cálculo de la moda para datos agrupados, extrayendo los siguientes datos:
 .
.
 .
.
 .
.



Mediana
Buscamos el intervalo donde se encuentra la mediana, para ello dividimos la  por
por  porque la mediana es el valor central,
porque la mediana es el valor central,
 .
.
Buscamos en la columna de las frecuencias acumuladas ( ) el intervalo que contiene a
) el intervalo que contiene a 
Clase de la mediana:  .
.
Aplicaremos la fórmula para el cálculo de la mediana para datos agrupados, extrayendo los siguientes datos:
 .
.
 .
.
 .
.
 .
.
 .
.
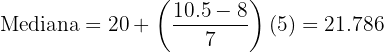 .
.
Media
Calculamos la sumatoria de la variable por su frecuencia absoluta ( ) que es
) que es  y la dividimos por
y la dividimos por 

Desviación media
Calculamos la sumatoria de de los productos de desviaciones respecto a la media por sus frecuencias absolutas correspondientes  que es
que es  y dividimos por
y dividimos por 

Varianza
Calculamos la sumatoria de  , la dividimos por
, la dividimos por  y al resultado le restaremos la media aritmética al cuadrado,
y al resultado le restaremos la media aritmética al cuadrado,  .
.

Desviación típica
Hacemos la raíz cuadrada de la varianza

Cuartiles
Cálculo del primer cuartil
Buscamos el intervalo donde se encuentra el primer cuartil, multiplicando  por
por  y dividiendo por
y dividiendo por 

Buscamos en la columna de las frecuencias acumuladas ( ) el intervalo que contiene a
) el intervalo que contiene a 
La clase de  es:
es: 
Aplicaremos la fórmula para el cálculo de cuartiles para datos agrupados, extrayendo los siguientes datos:





Cálculo del tercer cuartil
Buscamos el intervalo donde se encuentra el tercer cuartil, multiplicando  por
por  y dividiendo por
y dividiendo por 

Buscamos en la columna de las frecuencias acumuladas ( ) el intervalo que contiene a
) el intervalo que contiene a 
La clase de  es:
es: 
Aplicaremos la fórmula para el cálculo de cuartiles para datos agrupados, extrayendo los siguientes datos:





Deciles
Cálculo del tercer decil
Buscamos el intervalo donde se encuentra el tercer decil, multiplicando  por
por  y dividiendo por
y dividiendo por 

Buscamos en la columna de las frecuencias acumuladas ( ) el intervalo que contiene a
) el intervalo que contiene a 
La clase de  es:
es: 
Aplicaremos la fórmula para el cálculo de deciles para datos agrupados, extrayendo los siguientes datos:





Cálculo del sexto decil
Buscamos el intervalo donde se encuentra el sexto decil, multiplicando  por
por  y dividiendo por
y dividiendo por 

Buscamos en la columna de las frecuencias acumuladas ( ) el intervalo que contiene a
) el intervalo que contiene a 
La clase de  es:
es: 
Aplicaremos la fórmula para el cálculo de deciles para datos agrupados, extrayendo los siguientes datos:





Percentiles
El percentil  es igual al decil
es igual al decil 

Cálculo del percentil 70
Buscamos el intervalo donde se encuentra el percentil  , multiplicando
, multiplicando  por
por  y dividiendo por
y dividiendo por 

Buscamos en la columna de las frecuencias acumuladas ( ) el intervalo que contiene a
) el intervalo que contiene a 
La clase de  es:
es: 
Aplicaremos la fórmula para el cálculo de percentiles para datos agrupados, extrayendo los siguientes datos:





9Dada la distribución estadística:
 | |
 |  |
 |  |
 |  |
 |  |
 |  |
 |  |
Hallar:
a) La mediana y moda.
b) Cuartil  y
y  .
.
c) Media.
Dada la distribución estadística:
 | |
 |  |
 |  |
 |  |
 |  |
 |  |
 |  |
Calcular:
a) La mediana y moda.
b) Cuartil  y
y  .
.
c) Media.
Ampliamos la tabla con otra columna donde disponemos la frecuencia acumulada ( ):
):
En la primera casilla colocamos la primera frecuencia absoluta.
En la segunda casilla sumamos el valor de la frecuencia acumulada anterior más la frecuencia absoluta correspondiente y así sucesivamente hasta la última, que tiene que se igual a  .
.
 |  |  | |
 |  |  |  |
 |  |  |  |
 |  |  |  |
 |  |  |  |
 |  |  |  |
 |  |  | |
 |
Moda
En primer lugar buscamos el intervalo donde se encuentra la moda, que será el intervalo que tenga la mayor frecuencia absoluta ( )
)
La clase modal es: 
Aplicaremos la fórmula para el cálculo de la moda para datos agrupados, extrayendo los siguientes datos:
Límite inferior: 





Mediana
Buscamos el intervalo donde se encuentra la mediana, para ello dividimos la  por
por  porque la mediana es el valor central
porque la mediana es el valor central

Buscamos en la columna de las frecuencias acumuladas ( ) el intervalo que contiene a
) el intervalo que contiene a 
Clase de la mediana: 
Aplicaremos la fórmula para el cálculo de la mediana para datos agrupados, extrayendo los siguientes datos:





Cuartiles
Cálculo del primer cuartil
Buscamos el intervalo donde se encuentra el primer cuartil, multiplicando  por
por  y dividiendo por
y dividiendo por 

Buscamos en la columna de las frecuencias acumuladas ( ) el intervalo que contiene a
) el intervalo que contiene a 
La clase de  es:
es: 
Aplicaremos la fórmula para el cálculo de cuartiles para datos agrupados, extrayendo los siguientes datos:





Cálculo del tercer cuartil
Buscamos el intervalo donde se encuentra el tercer cuartil, multiplicando  por
por  y dividiendo por
y dividiendo por 

Buscamos en la columna de las frecuencias acumuladas  ) el intervalo que contiene a
) el intervalo que contiene a 
La clase de  es:
es: 
Aplicaremos la fórmula para el cálculo de cuartiles para datos agrupados, extrayendo los siguientes datos:





Media
No se puede calcular la media, porque no se puede hallar la marca de clase del último intervalo.
Si quieres que tus hijos refuercen esta asignatura, no lo dudes y entra Superprof para encontrar clases de matematicas primaria o, si lo prefieres, un profesor de matematicas online.













Apuntes es una plataforma dirigida al estudio y la práctica de las matemáticas a través de la teoría y ejercicios interactivos que ponemos a vuestra disposición. Esta información está disponible para todo aquel/aquella que quiera profundizar en el aprendizaje de esta ciencia. Será un placer ayudaros en caso de que tengáis dudas frente algún problema, sin embargo, no realizamos un ejercicio que nos presentéis de 0 sin que hayáis si quiera intentado resolverlo. Ánimo, todo esfuerzo tiene su recompensa.
Media de 30. 35. 30. 40. 35. 30. 35.
suma los datos y nos da 235 a eso le dividimos el numero de datos que es 7 se divide 235 entre 7 =33.5 esa es la media o el promedio
Que tanto% de las inversiones establecidas por el empresario entran comprendidas a más de 3.5 desviaciones estándar y a menos de 3.5 desviaciones estándar respecto a la media según el teorema de Chevichev
Segun chevichev seria un 35% al dividirlo entre cien y calculandolo en porcenteaje con la regla de Evalis
Me pueden ayudar por favor.
Necesito determinar la desviación media del siguiente grupo de números en relación al total de las observaciones: 10, 8, 7, 9, 6.
Gracias.):
Al calcular la media y la desviación estándar de 50 datos, ambos resultaron ser iguales a 12. Un chequeo de los datos mostró que en lugar de un dato con valor de 12,8 se había introducido 17,8; corrija la media y la desviación estándar.
Desviación y varianza y tipica12..6..7.3.15.10.18.5