Temas

Definición de deciles
Los deciles son los nueve valores que dividen una serie de datos ordenados en diez partes iguales.
Los deciles dan los valores correspondientes al  %, al
%, al  %... y al
%... y al  % de los datos.
% de los datos.
El quinto decil coincide con la mediana: . Pero también, coincide con el segundo cuartil:
. Pero también, coincide con el segundo cuartil: .
.
Cálculo de los deciles
En primer lugar buscamos la clase donde se encuentra  , en la tabla de las frecuencias acumuladas.
, en la tabla de las frecuencias acumuladas.

 es el límite inferior de la clase donde se encuentra el decil i-ésimo.
es el límite inferior de la clase donde se encuentra el decil i-ésimo.
 es la suma de las frecuencias absolutas.
es la suma de las frecuencias absolutas.
 es la frecuencia acumulada anterior a la clase el decil i-ésimo.
es la frecuencia acumulada anterior a la clase el decil i-ésimo.
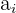 es la amplitud de la clase o longitud del intervalo correspondiente a la clase del decil i-ésimo.
es la amplitud de la clase o longitud del intervalo correspondiente a la clase del decil i-ésimo.
Ejercicio de deciles
Calcular los deciles de la distribución de la tabla.
 | |
|---|---|
 |  |
 |  |
 |  |
 |  |
 |  |
 |  |
 |  |
Solución:
En primer lugar crearemos una nueva columna con los valores de la frecuencia acumulada. Para obtener la frecuencia acumulada realizamos lo que se indica:
En la primera casilla colocamos la primera frecuencia absoluta. En la segunda casilla sumamos el valor de la frecuencia acumulada anterior más la frecuencia absoluta correspondiente y así sucesivamente hasta la última, que tiene que ser igual a 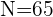 .
.
 |  | ||
|---|---|---|---|
 |  |  | |
 |  |  | |
 |  |  | |
 |  |  | |
 |  |  | |
 |  |  | |
 |
|  | |
 |
Cálculo del primer decil
Buscamos la clase donde se encuentra el primer decil:
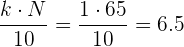
Buscamos en la columna de las frecuencias acumuladas  el intervalo que contiene a
el intervalo que contiene a  .
.
La clase de  es:
es: 
Aplicaremos la fórmula para el cálculo de deciles para datos agrupados, extrayendo los siguientes datos:

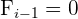
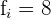
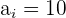
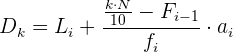
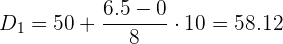
Cálculo del segundo decil
Buscamos la clase donde se encuentra el primer decil:
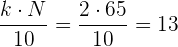
Buscamos en la columna de las frecuencias acumuladas  el intervalo que contiene a
el intervalo que contiene a  .
.
La clase de  es:
es: 
Aplicaremos la fórmula para el cálculo de deciles para datos agrupados, extrayendo los siguientes datos:
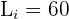
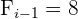
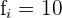
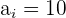
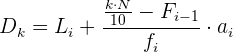
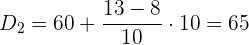
Cálculo del tercer decil
Buscamos la clase donde se encuentra el primer decil:

Buscamos en la columna de las frecuencias acumuladas  el intervalo que contiene a
el intervalo que contiene a 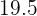 .
.
La clase de  es:
es: 
Aplicaremos la fórmula para el cálculo de deciles para datos agrupados, extrayendo los siguientes datos:
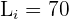
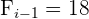
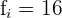
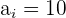
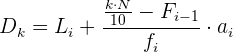
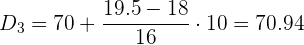
Cálculo del cuarto decil
Buscamos la clase donde se encuentra el primer decil:
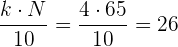
Buscamos en la columna de las frecuencias acumuladas  el intervalo que contiene a
el intervalo que contiene a  .
.
La clase de  es:
es: 
Aplicaremos la fórmula para el cálculo de deciles para datos agrupados, extrayendo los siguientes datos:
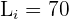
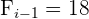
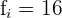
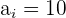
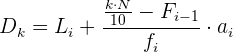
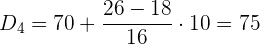
Cálculo del quinto decil
Buscamos la clase donde se encuentra el primer decil:

Buscamos en la columna de las frecuencias acumuladas  el intervalo que contiene a
el intervalo que contiene a  .
.
La clase de  es:
es: 
Aplicaremos la fórmula para el cálculo de deciles para datos agrupados, extrayendo los siguientes datos:
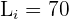
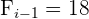
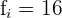
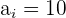
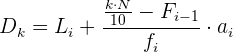
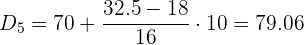
Cálculo del sexto decil
Buscamos la clase donde se encuentra el primer decil:
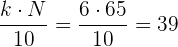
Buscamos en la columna de las frecuencias acumuladas  el intervalo que contiene a
el intervalo que contiene a  .
.
La clase de  es:
es: 
Aplicaremos la fórmula para el cálculo de deciles para datos agrupados, extrayendo los siguientes datos:
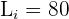
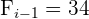
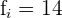
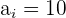
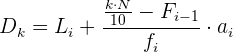

Cálculo del séptimo decil
Buscamos la clase donde se encuentra el primer decil:
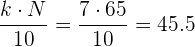
Buscamos en la columna de las frecuencias acumuladas  el intervalo que contiene a
el intervalo que contiene a  .
.
La clase de  es:
es: 
Aplicaremos la fórmula para el cálculo de deciles para datos agrupados, extrayendo los siguientes datos:
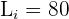
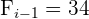
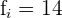
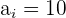
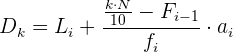
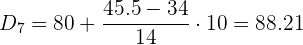
Cálculo del octavo decil
Buscamos la clase donde se encuentra el primer decil:

Buscamos en la columna de las frecuencias acumuladas  el intervalo que contiene a
el intervalo que contiene a  .
.
La clase de 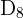 es:
es: 
Aplicaremos la fórmula para el cálculo de deciles para datos agrupados, extrayendo los siguientes datos:


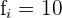
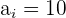
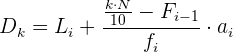

Cálculo del noveno decil
Buscamos la clase donde se encuentra el primer decil:
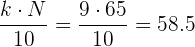
Buscamos en la columna de las frecuencias acumuladas  el intervalo que contiene a
el intervalo que contiene a  .
.
La clase de  es:
es: 
Aplicaremos la fórmula para el cálculo de deciles para datos agrupados, extrayendo los siguientes datos:


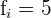
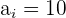
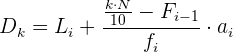














Apuntes es una plataforma dirigida al estudio y la práctica de las matemáticas a través de la teoría y ejercicios interactivos que ponemos a vuestra disposición. Esta información está disponible para todo aquel/aquella que quiera profundizar en el aprendizaje de esta ciencia. Será un placer ayudaros en caso de que tengáis dudas frente algún problema, sin embargo, no realizamos un ejercicio que nos presentéis de 0 sin que hayáis si quiera intentado resolverlo. Ánimo, todo esfuerzo tiene su recompensa.
Media de 30. 35. 30. 40. 35. 30. 35.
suma los datos y nos da 235 a eso le dividimos el numero de datos que es 7 se divide 235 entre 7 =33.5 esa es la media o el promedio
Que tanto% de las inversiones establecidas por el empresario entran comprendidas a más de 3.5 desviaciones estándar y a menos de 3.5 desviaciones estándar respecto a la media según el teorema de Chevichev
Segun chevichev seria un 35% al dividirlo entre cien y calculandolo en porcenteaje con la regla de Evalis
Me pueden ayudar por favor.
Necesito determinar la desviación media del siguiente grupo de números en relación al total de las observaciones: 10, 8, 7, 9, 6.
Gracias.):
Al calcular la media y la desviación estándar de 50 datos, ambos resultaron ser iguales a 12. Un chequeo de los datos mostró que en lugar de un dato con valor de 12,8 se había introducido 17,8; corrija la media y la desviación estándar.
Desviación y varianza y tipica12..6..7.3.15.10.18.5