Temas

Pasos para resolver inecuaciones de segundo grado
Lo primero que debemos hacer, es recordar ciertas propiedades de las ecuaciones de segundo grado, relacionadas con su tipo de soluciones:
Es posible conocer el tipo de soluciones que tendrá una ecuación de segundo grado
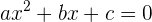
si es que tenemos el signo de su discriminante
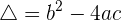 .
.
donde hay tres casos posibles:
- Si
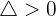 , entonces hay dos soluciones reales distintas
, entonces hay dos soluciones reales distintas
- Si
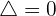 , entonces hay una única solución real, con multiplicidad dos
, entonces hay una única solución real, con multiplicidad dos
- Si
 , entonces no tiene solucion real
, entonces no tiene solucion real
Esta información será de utilidad, ya que nos permitirá realizar un proceso muy simple para conocer la solución de inecuaciones de segundo grado.
Es importante también, hacer notar que en términos generales, el proceso de solución de la inecuación consiste en:
- Encontrar las soluciones de la ecuación
- Ubicarlas en la recta real e identificar las secciones generadas
- Conocer el signo del polinomio en cada una de las secciones generadas
- Buscar la solución de la inecuación
Y en dado caso que la ecuación no tenga solución real, no se secciona a la recta real, sin embargo también se busca el signo del polinomio y el proceso es análogo.
Entonces, dependiendo del signo del discriminante aplicaremos un proceso a seguir, por tal razón dividiremos el proceso en tres casos.
Primer caso: 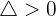
Vamos a resolver la inecuación: 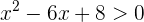
Ahora, debemos conocer el signo del discriminante
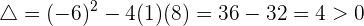
significa que existen dos soluciones reales distintas de la ecuación (o raíces del polinomio), y entonces ahora sigamos este proceso:
1Encontrar las soluciones de la ecuación
Igualamos con cero al polinomio 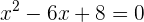
Factorizamos 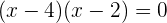
Y entonces las soluciones son: 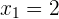 y
y 
vemos que las soluciones son raíces reales distintas porque el discriminante es mayor que cero.
2 Ubicarlas en la recta real e identificar las secciones generadas
Primero, ubicamos los valores obtenidos en la recta real, colocamos encima de ellos dos círculos vacíos con la finalidad de representar geométricamente, que en la inecuación no se permite la igualdad con cero, y además observamos que se generan tres regiones

La razón de esto es la siguiente:
Si  , entonces el polinomio valuado en las soluciones, da como resultado cero
, entonces el polinomio valuado en las soluciones, da como resultado cero
y por otro lado la inecuación  al ser estrictamente mayor que cero, no admite valores
al ser estrictamente mayor que cero, no admite valores  que al evaluarlos en el polinomio, el resultado genere un cero, en este caso son justamente
que al evaluarlos en el polinomio, el resultado genere un cero, en este caso son justamente 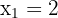 y
y  .
.
Por esta razón se ponen los círculos vacíos, para quitar a los valores que no admite la inecuación y tomarlos únicamente como referencia.
En caso contrario, de admitir la inecuación iguadad con cero, se colocan círculos rellenos.
3 Conocer el signo del polinomio en cada una de las secciones generadas
Como observamos en el paso anterior, se generaron tres secciones, así que por cada una de ellas seleccionemos a uno de sus valores y evaluemos en el polinomio para conocer su signo:
- Para
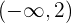 , podemos seleccionar
, podemos seleccionar  y evaluarlo en el polinomio
y evaluarlo en el polinomio 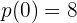 , resultando un valor positivo.
, resultando un valor positivo.
- Para
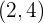 , podemos seleccionar
, podemos seleccionar 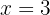 y evaluarlo en el polinomio
y evaluarlo en el polinomio 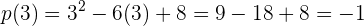 , resultando un valor negativo.
, resultando un valor negativo.
- Para
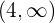 , podemos seleccionar
, podemos seleccionar  y evaluarlo en el polinomio
y evaluarlo en el polinomio 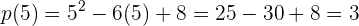 , resultando un valor positivo.
, resultando un valor positivo.
esto significa que
- Para todo elemento
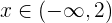 , el polinomio
, el polinomio  siempre tendrá valores positivos
siempre tendrá valores positivos
- Para todo elemento
 , el polinomio
, el polinomio  siempre tendrá valores negativos
siempre tendrá valores negativos
- Para todo elemento
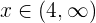 , el polinomio
, el polinomio  siempre tendrá valores positivos
siempre tendrá valores positivos

4Buscar la solución de la inecuación
Con la información que hemos generado hasta ahora, ya podemos encontrar la solución de la inecuación
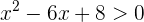
es decir, valores dentro de la recta real que al evaluarlos en el polinomio  el resultado final que se obtenga debe de ser positivo, además distinto de cero. Entonces sólo hace falta buscar las regiones que cumplen la condición
el resultado final que se obtenga debe de ser positivo, además distinto de cero. Entonces sólo hace falta buscar las regiones que cumplen la condición
En otras palabras, la solución es:

Variaciones posibles
1Si la ecuación fuese 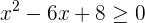 , significa que ahora si se admiten valores que al evaluarlos en el polinomio el resultado sea cero, razón por la que incluimos al dos y al cuatro, entonces la solución sería:
, significa que ahora si se admiten valores que al evaluarlos en el polinomio el resultado sea cero, razón por la que incluimos al dos y al cuatro, entonces la solución sería:
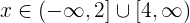
2Si la ecuación fuese 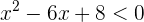 , la solución sería:
, la solución sería:

3 Si la ecuación fuese 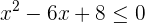 , la solución sería:
, la solución sería:
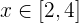
Segundo caso: 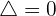
Vamos a resolver la inecuación: 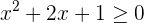
Ahora, debemos conocer el signo del discriminante
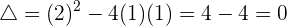
significa que existe una sola solución real, y entonces ahora sigamos este proceso:
1Encontrar la solucion de la ecuación
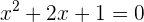
Si factorizamos  , nos damos cuenta de que la solución es
, nos damos cuenta de que la solución es 
2 Ubicarla en la recta real e identificar las secciones generadas
En este caso como tenemos a una solución, se generan dos secciones en la recta real
 y
y 
3 Conocer el signo del polinomio en cada una de las secciones generadas
En este caso basta con conocer el signo del polinomio 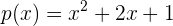 en alguno de los puntos de cualquiera de las dos secciones, ya que para ambas será el mismo resultado.
en alguno de los puntos de cualquiera de las dos secciones, ya que para ambas será el mismo resultado.
Si  entonces
entonces 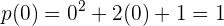 , el cual es un resultado positivo, significa que:
, el cual es un resultado positivo, significa que:
- Si
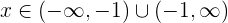 entonces
entonces 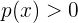
- Si
 entonces
entonces 
4Buscar la solución de la inecuación
Como recordamos, la inecuación
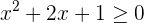
tiene como solución, a valores de la recta real  , tales que al evaluarlos en el polinomio
, tales que al evaluarlos en el polinomio 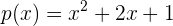 el resultado final sea un número mayor o igual a cero, significa que de la información obtenida, nuestra solución es
el resultado final sea un número mayor o igual a cero, significa que de la información obtenida, nuestra solución es

Variaciones posibles
| Inecuación | Factorización | Solución |
|---|---|---|
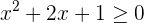 | 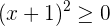 | 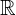 |
 | 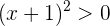 |  |
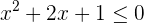 |  |  |
 | 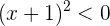 |  |
Tercer caso: 
Vamos a resolver la inecuación: 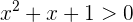
Ahora, debemos conocer el signo del discriminante
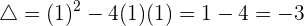
significa que no existe solución real, significa que ahora no se generan secciones, y entonces seguimos este proceso:
1 Escogemos a cualquier valor real y lo evaluamos en el polinomio para conocer el signo.
Escogemos a  y lo evaluamos en el polinomio
y lo evaluamos en el polinomio
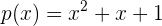
quedando como resultado 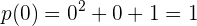 el cual es un valor positivo.
el cual es un valor positivo.
Esto nos informa que para todo 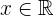 el polinomio
el polinomio 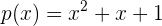 siempre será positivo.
siempre será positivo.
2Buscar la solución de la inecuación
Como buscamos la solución de la inecuación 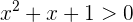 , y ya sabemos que cualquier número real
, y ya sabemos que cualquier número real  que sea ocupado para calcular
que sea ocupado para calcular  siempre nos dará como resultado un número positivo, entonces todo número real se convierte en solución de la inecuación.
siempre nos dará como resultado un número positivo, entonces todo número real se convierte en solución de la inecuación.
Si en dado caso, la inecuación fuese  , entonces la solución es vacío, ya que no hay número real
, entonces la solución es vacío, ya que no hay número real  que al ocuparlo para calcular
que al ocuparlo para calcular  no dé como resultado algún negativo, que es como lo pide la inecuación.
no dé como resultado algún negativo, que es como lo pide la inecuación.
Variaciones posibles
| Solución | |
|---|---|
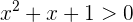 | 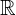 |
 | 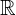 |
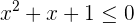 |  |
 |  |
Pasos para resolver inecuaciones racionales
Las inecuaciones racionales se resuelven de un modo similar a las de segundo grado, pero hay que tener presente que el denominador no puede ser cero.
Vamos a resolver la inecuación:

1Hallamos las raíces del numerador y del denominador.
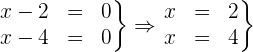
2 Representamos estos valores en la recta real, teniendo en cuenta que las raíces del denominador, independientemente del signo de la desigualdad, tienen que ser abiertas.

3 Tomamos un punto de cada intervalo y evaluamos el signo en cada intervalo
Consideremos
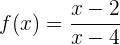
Ahora evaluemos en algún punto de cada uno de los intervalos generados, tomando en cuenta que no se puede evaluar en 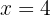 porque en ese lugar se indetermina la fracción, y recordando que
porque en ese lugar se indetermina la fracción, y recordando que 
- Si tomamos a
 del intervalo
del intervalo 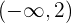 , tenemos que
, tenemos que
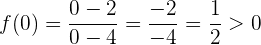
el cual es un valor positivo
- Si tomamos a
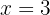 del intervalo
del intervalo 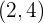 , tenemos que
, tenemos que
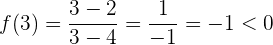
el cual es un valor negativo
- Si tomamos a
 del intervalo
del intervalo 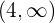 , tenemos que
, tenemos que
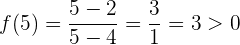
el cual es un valor positivo

4 La solución está compuesta por los intervalos (o el intervalo) que tengan el mismo signo que la fracción polinómica.
Ahora con esta información, ya podemos encontrar la solución, basta con tomar los intervalos que generan el mismo signo que tiene la inecuacion racional, es decir positivo e igual a cero, veamos:
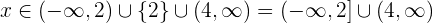
El 4 está abierto porque es una raíz del denominador y no puede ser cero el denominador
Variaciones posibles
1 Si la ecuación fuese

la solución sería:

2 Si la ecuación fuese

la solución sería:

3 Si la ecuación fuese
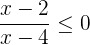
la solución sería:
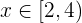
Ejemplo de inecuación resuelta
Vamos a resolver la inecuación:
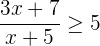
1 Pasamos el 5 al primer miembro y desarrollamos la fracción
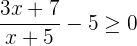
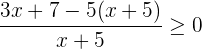
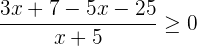
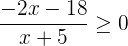
2 Hallamos las raíces del numerador y del denominador
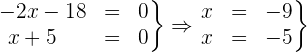

3 Evaluamos para conocer el signo en cada región, proponiendo un valor representativo de cada una de ellas:
- Si tomamos a
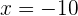 del intervalo
del intervalo 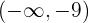 , tenemos que
, tenemos que
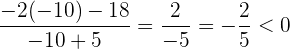
el cual es un valor negativo
- Si tomamos a
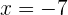 del intervalo
del intervalo  , tenemos que
, tenemos que

el cual es un valor positivo
- Si tomamos a
 del intervalo
del intervalo 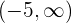 , tenemos que
, tenemos que
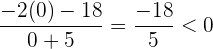
el cual es un valor negativo
4La solución se encuentra seleccionando a los intervalos que generan el mismo signo que la inecuación propuesta, es decir mayor o igual que cero
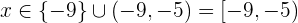










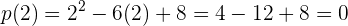




Apuntes es una plataforma dirigida al estudio y la práctica de las matemáticas a través de la teoría y ejercicios interactivos que ponemos a vuestra disposición. Esta información está disponible para todo aquel/aquella que quiera profundizar en el aprendizaje de esta ciencia. Será un placer ayudaros en caso de que tengáis dudas frente algún problema, sin embargo, no realizamos un ejercicio que nos presentéis de 0 sin que hayáis si quiera intentado resolverlo. Ánimo, todo esfuerzo tiene su recompensa.
INECUACION CUADRATICA RESOLVER x^2 − 4x + 7 > 0
Necesito ayuda con este problema 2x<(2x+1)(x-2)-2x(x-7)
Xfi
Por favor ayúdenme con este ejercicio que hay que resolver por medio de inecuaciones.
En un depósito cada tanque de leche tiene una capacidad de 200 litros. ¿Cuál es la cantidad máxima de tanques que puede cargar un camión cuya capacidad es de 50000 litros de leche?
necesito ayuda con esta inecuacion cuadratica: -2x al cuadrado +18x-36>0
×-18al cuadrado mas o menos√18al cuadrado-4(-2)(-36) dividido entre2×(-2)
×18mas o menos√18+-144. Dividido por-4
×18mas o menos√-126÷-4
×18+63/-4. × 18+63/-4. ×18-63)-4
×81/-4. ×-45/-4
×=-20,25. ×=11,25
Deberías hacer una tabla de valores para poder estudiar el signo y después escoger las soluciones adecuadas
Necesito q me respondan a esta ecuación
X²(x+4)
______>0
(X+1)(x+2)