Racionaliza y simplifica el resultado siempre que se pueda. Recuerda usar el símbolo √ en los resultados:
| 1 |  |  | |
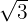 |
Multiplicamos numerador y denominador por raíz de 
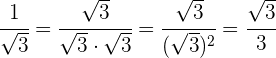
| 2 |  |  | · |
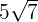 |
Multiplicamos numerador y denominador por raíz de 
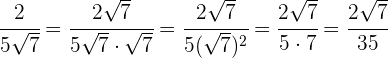
| 3 |  |  | |
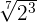 |
Tenemos que multiplicar en el numerador y denominador por la raíz séptima de 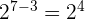
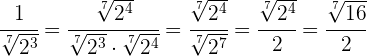
| 4 |  |  | · |
 |
La base del radicando  lo ponemos en forma de potencia:
lo ponemos en forma de potencia: 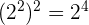
Tenemos que multiplicar en el numerador y denominador por la raíz quinta de  , realizamos las operaciones y simplificamos la fracción
, realizamos las operaciones y simplificamos la fracción

| 5 |  |  |  |
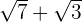 |
Multiplicamos numerador y denominador por el conjugado del denominador y efectuamos la suma por diferencia en el denominador, por lo que obtenemos una diferencia de cuadrados

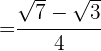
| 6 |  |  | ·  |
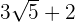 |
Multiplicamos numerador y denominador por el conjugado del denominador y efectuamos la suma por diferencia en el denominador, por lo que obtenemos una diferencia de cuadrados
Multiplicamos en el numerador y restamos en el denominador

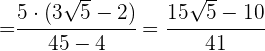
| 7 |  |  | ·  · · |
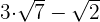 |
Multiplicamos numerador y denominador por el conjugado del denominador y efectuamos la suma por diferencia en el denominador, por lo que obtenemos una diferencia de cuadrados
Multiplicamos en el numerador y operamos en el denominador

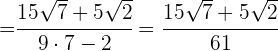
| 8 | 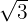 |  |  |
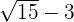 |
Multiplicamos numerador y denominador por el conjugado del denominador y efectuamos la suma por diferencia en el denominador, por lo que obtenemos una diferencia de cuadrados
En el numerador multiplicamos por raíz de  el paréntesis:
el paréntesis:
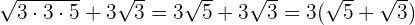
En el denominador efectuamos las operaciones indicadas y por último simplificamos la fracción

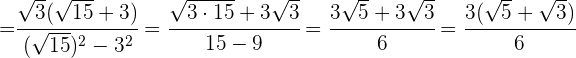
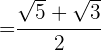
Si tienes dudas puedes consultar la teoría



Apuntes es una plataforma dirigida al estudio y la práctica de las matemáticas a través de la teoría y ejercicios interactivos que ponemos a vuestra disposición. Esta información está disponible para todo aquel/aquella que quiera profundizar en el aprendizaje de esta ciencia. Será un placer ayudaros en caso de que tengáis dudas frente algún problema, sin embargo, no realizamos un ejercicio que nos presentéis de 0 sin que hayáis si quiera intentado resolverlo. Ánimo, todo esfuerzo tiene su recompensa.
porque surge una fraccion mixta del caso uno ejemplo 2 alguien me podria explicar
Me aparecen desigualdades en el ejemplo que mencionas y ninguna fracción.
Tengo aquí una duda
Sabemos que no existen raíces de negativos, solo en los complejos
Entonces supongamos que estamos en los complejos y no en los reales la propiedad de la multiplicacion de radicales se cumple? Lo comento porque en lo
Raíz de (-4) × raíz de (-9)
Si lo hacemos por separado da – 6
Pues obtenemos (2i)(3i)
Pero si aplicamos la propiedad da como resultado 6
Cuál es la correcta?
Si se multiplica 2i x 3 i se obtiene 6 i^2, pero i^2 = -1
Entonces el resultado es – 6
Si te refieres al ejercicio |x-2|>=1, el resultado es correcto el método puede no ser claro.
Se recomienda tomar por casos, a) x-2>=1 y b) x-2<=-1 se resuelve cada uno y el resultado concuerda con lo mostrado.
En el ejercicio 3 no me aparece ningún 24 y 8.