Temas

Operaciones variadas con números enteros
Ordenar, en sentido creciente, representar gráficamente, y calcular los opuestos y valores absolutos de los siguientes números enteros:
8, −6, −5, 3, −2, 4, −4, 0, 7
¿Buscas clases particulares matematicas madrid?
Ordenar en sentido creciente , representar gráficamente, y calcular los opuestos y valores absolutos de los siguientes números:
8, −6, −5, 3, − 2, 4, −4, 0, 7
Solución:
− 6 < − 5 < − 4 < − 2 < 0 < 3 < 4 < 7 < 8

Cálculo de los opuestos y valores absolutos:
1 (−6) = −(−6) = 6 |−6| = 6
2 (−5) = −(−5) = 5 |−5| = 5
3 (−4) = −(−4) = 4 |−4| = 4
4 (−2) = −(−2) = 2 |−2| = 2
5 (0) = |0| = 0
6 (3) = −3 |3| = 3
7 (4) = −4 |4| = 4
8 (7) = −7 |7| = 7
9 (8) = −8 |8| = 8
Obtén más ejercicios en clases particulares matematicas.
Valor absoluto y valor opuesto
Representar gráficamente, y calcular los opuestos y valores absolutos de los siguientes números enteros:
−4, 6, −2, 1, −5, 0, 9
Representar gráficamente, y calcular los opuestos y valores absolutos de los siguientes números enteros:
−4, 6, −2, 1, −5, 0, 9
Solución:

Cálculo de los opuestos y valores absolutos:
1 (−4) = −(−4) = 4 |−4| = 4
2 (6) = −6 |6| = 6
3 (−2) = −(−2) = 2 |−2| = 2
4 (1) = −1 |1| = 1
5 (−5) = −(−5) = 5 |−5| = 5
6 (0) = |0| = 0
7 (9) = −9 |9| = 9
Aprende sin moverte de casa con nuestras clases de matematicas online.
Factorizar
Sacar factor común en las expresiones:
1 3 · 2 + 3 · (−5) =
2 (−2) · 12 + (−2) · (−6) =
3 8 · 5 + 8 =
4 (−3) · (−2) + (−3) · (−5) =
Sacar factor común en las expresiones:
Nota: Para este ejercicio haremos uso de la propiedad distributiva a(b+c)= a·b + a·c
1 Solución directa: 3 · 2 + 3 · (−5) = 6 + (-15)= 6 - 15 = - 9
Factorización : Podemos observar que el factor común es el 3, lo extraemos usando la propiedad distributiva
3( 2 + (-5) )
Comprobación :
3(2+(-5)) = 3(2-5)=3(-3)= 9
2 (−2) · 12 + (−2) · (−6) = - 24 + 12 = -12
Factorización : Podemos observar que el factor común es el -2, lo extraemos usando la propiedad distributiva
-2( 12 + (-6) )
Comprobación :
-2( 12 + (-6) ) = -2( 12-6)= -2(6)=-12
3 8 · 5 + 8 = 40 + 8 = 48
Factorización : Podemos observar que el factor común es el 8, lo extraemos usando la propiedad distributiva
8( 5+1 )
Comprobación :
8( 5+1 ) =8(6)=48
4 (−3) · (−2) + (−3) · (−5) = 6 + 15 = 21
Factorización : Podemos observar que el factor común es el -3, lo extraemos usando la propiedad distributiva
-3( (-2)+(-5) )
Comprobación :
-3( (-2)+(-5) ) = -3(-2-5)= -3(-7)=21
Operaciones básicas con numero enteros
Realizar las siguientes operaciones con números enteros:
1 (3 − 8) + [5 − (−2)]
2 5 − [6 − 2 − (1 − 8) −3 + 6] + 5
3 9 : [6 : (− 2)]
4 [(−2)5 − (−3)³]²
5 (5 + 3 · 2 : 6 − 4 ) · (4 : 2 − 3 + 6) : (7 − 8 : 2 − 2)²
6 [(17 − 15)³ + (7 − 12)²] : [(6 − 7) · (12 − 23)]
Realizar las siguientes operaciones con números enteros:
Soluciones:
1 (3 − 8) + [5 − (−2)] =
Escribimos el opuesto de (−2)
= −5 + (5 + 2) =
Operamos en el paréntesis
= −5 + 7 = 2
2 5 − [6 − 2 − (1 − 8) − 3 + 6] + 5 =
Operamos en paréntesis
= 5 − [6 − 2 − (−7) − 3 + 6] + 5 =
Calculamos el opuesto de (−7)
= 5 − (6 − 2 + 7 − 3 + 6) + 5 =
Operamos en el paréntesis y tomamos el opuesto del resultado
= 5 − 14 + 5 = −4
3 9 : [6 : (−2)] =
Realizamos la división del corchete
= 9 : (−3) = −3
4 [(−2)5 − (−3)³]² =
Realizamos las potencias de los paréntesis. Para (−2)5 calculamos de la manera siguiente: (-2)(-2) = 4. 4(-2) = -8. -8 (-2) = 16. 16 (-2) = -32. Para (−3)³, siguiendo la misma manera de calcular, tenemos (-3)(-3) = 9. 9 (-3) = -27
= [−32 − (−27)]² =
Dehacemos paréntesis
= (−32 + 27)² =
Realizamos la operación y elevamos al cuadrado
= (−5)² = 25
5 (5 + 3 · 2 : 6 − 4 ) · (4 : 2 − 3 + 6) : (7 − 8 : 2 − 2)² =
Realizamos 3 · 2 (primero haremos la multiplicación) y las divisiones
= (5 + 6 : 6 − 4 ) · (2 − 3 + 6) : (7 − 4 − 2)² =
Efectuamos la división
= (5 + 1 − 4 ) · (2 − 3 + 6) : (7 − 4 − 2)² =
Operamos en cada paréntesis
= 2 · 5 : 1² =
Elevamos al cuadrado
= 2 · 5 : 1 =
Primero tenemos que multiplicar y después dividiremos
= 10 : 1 =10
6 [(17 − 15)³ + (7 − 12)²] : [(6 − 7) · (12 − 23)]
Operamos en los paréntesis
= [(2)³ + (−5)²] : [(−1) · (−11)]
Realizamos las potencias
= (8 + 25) : [(−1) · (−11)] =
Operamos en el paréntesis y en el corchete y dividimos los resultados
= 33 : 11 = 3
Jerarquía de operaciones
Realizar las siguientes operaciones con números enteros:
1(7 − 2 + 4) − (2 − 5)
2 1 − (5 − 3 + 2) − [5 − (6 − 3 + 1) − 2]
3 −12 · 3 + 18 : (−12 : 6 + 8)
42 · [( −12 + 36) : 6 + (8 − 5) : (−3)] - 6
5 [(−2)5 · (−3)2] : (−2)2 = (−32 · 9) : 4
6 6 + {4 − [(17 − (4 · 4)] + 3} − 5
Realizar las siguientes operaciones con números enteros:
Soluciones:
1 (7 − 2 + 4) − (2 − 5) =
Operamos en los paréntesis
= 9 − (−3) =
Tomamos el opuesto de (−3)
= + 3 = 12
2 1 − (5 − 3 + 2) − [5 − (6 − 3 + 1) − 2] =
Operamos en los paréntesis
= 1 − (4) − [5 − (4) − 2] =
Tomamos los opuestos de los dos 4
= 1 − 4 − (5 − 4 − 2) =
Operamos el paréntesis
= 1 − 4 − 5 + 4 + 2 =
Sumamos el 4 con su inverso
= 1 − 5 + 2 = −2
3 −12 · 3 + 18 : (−12 : 6 + 8) =
Realizamos la división del paréntesis
= − 12 · 3 + 18 : (−2 + 8) =
Operamos en el paréntesis
= −12 · 3 + 18 : 6 =
Realizamos la multiplicación y la división
= −36 + 3 = −33
4 2 · [( −12 + 36) : 6 + (8 − 5) : (−3)] − 6 =
Realizamos las operaciones en los dos primeros paréntesis
= 2 · [24 : 6 + 3 : (−3)] − 6 =
Efectuamos las divisiones
= 2 · [ 4 + (−1)] − 6 =
Operamos en el corchete
= 2 · 3 − 6 =
Hacemos el producto
= 6 − 6 = 0
5 [(−2)5 · (−3)²] : (−2)² =
Realizamos las potencias
= (−32 · 9) : 4 =
Operamos en el paréntesis
= −288 : 4 = −72
6 6 + {4 − [(17 − (4 · 4)] + 3} − 5 =
Realizamos el producto
= 6 + [4 − (17 − 16) + 3] − 5 =
Operamos en el paréntesis y le hacemos el opuesto
= 6 + (4 − 1 + 3) − 5 =
Operamos en el paréntesis
= 6 + 6 − 5 = 7
Soluciones fuera y dentro del conjunto de números reales
Calcula el resultado de la potencia y después verifica si dicho resultado tiene raíz cuadrada existente en los números reales:
1 (−9)²
2 (−1)7
3 (−3)² · (−3)
4 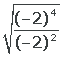
5 (−2)³
6 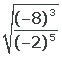
Calcula el resultado de la potencia y después verifica si dicho resultado tiene raíz cuadrada existente en los números reales:
Soluciones:
1 (−9)² = 81
La raíz cuadrada de 81 es ± 9
2 (−1)7 = −1
La raíz cuadrada de -1 no existe en los reales, por lo tanto dicha raíz no tiene solución en el conjunto de los números reales
En general, no existe la raíz cuadrada de un número negativo porque no existe ningún número que elevado al cuadrado tenga signo negativo
3 (−3)² · (−3) =
Realizamos el producto de las potencias y elevamos al cubo
= (−3)³ = −27
La raíz cuadrada de -27 no tiene solución
4 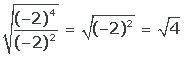
Realizamos la división de potencias, elevamos al cuadrado y extraemos la raíz
El resultado es 2, y si existe la raíz cuadrada de 2 en los números reales.
5 (−2)³ = −8
La raíz cuadrada de -8 no tiene solución en los reales
6 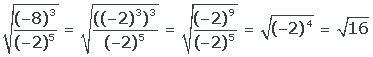
Ponemos 8 en forma de potencia, realizamos la potencia de una potencia en el numerador, dividimos las potencias, elevamos a la cuarta y extraemos la raíz
El resultado es 4, y la raiz cuadrada de 4 es ±2.
Operaciones con potencias
Realizar las siguientes operaciones con potencias de números enteros:
1 (−2)² · (−2)³ · (−2)4
2 (−8) · (−2)² · (−2)0 (−2)
3(−2)−2 · (−2)³ · (−2)4
4 2−2 · 2−3 · 24
5 2² : 2³
6 2-2 : 2³
7 2² : 2-3
8 2-2 : 2-3
9 [(−2)− 2] 3 · (−2)³ · (−2)4
10[(−2)6 : (−2)³]³ · (−2) · (−2)−4
Realizar las siguientes operaciones con potencias:
Soluciones:
Nota: Para resolver estos ejercicios se utilizaran las leyes de los exponentes
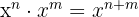
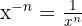

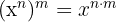
1 (−2)² · (−2)³ · (−2)4 = (−2)9 = −512
El resultado tendrá signo negativo porque la base es negativa y el exponente es impar
2 (−8) · (−2)² · (−2)0 (−2) =
Primero descomponemos el 8 en factores
(−2)³ · (−2)² · (−2)0 · (−2) = (−2)6 = 64
El resultado tendrá signo positivo porque la base es negativa y el exponente es par
3 (−2)−2 · (−2)³ · (−2)4 = (−2)5 = −32
4 2−2 · 2−3 · 24 = 2−1 = 1/2
Al ser negativo el exponente tenemos que tomar el inverso de la base, es decir, aplicar la ley de signos correspondiente
5 2² : 2³ = 2−1 = 1/2
Al ser negativo el exponente tenemos que tomar el inverso de la base, es decir, aplicar la ley de signos correspondiente
6 2−2 : 2³ = 2−5 = 1/25 = 1/32
7 2² : 2−3 = 25 = 32
8 2−2 : 2−3 = 2
9 [(−2)−2]³ · (−2)³ · (−2)4 = (−2)−6 · (−2)7 = −2
10 [(−2)6 : (−2)³] 3 · (−2)· (−2)−4 = [(−2)³]³ · (−2)−3 = (−2)9 · (−2)−3= (−2)6 = 64
Uso de exponentes en operaciones con enteros
Realizar las siguientes operaciones con potencias de números enteros:
1 (−3)1 · (−3)³ · (−3)4 =
2(−27) · (−3) · (−3)² · (−3)0=
3 (−3)² · (−3)³ · (−3)−4 =
4 3−2 · 3−4 · 34 =
5 5² : 5³ =
6 5-2 : 5³ =
7 5² : 5-3 =
8 5-2 : 5-3 =
9 (−3)1 · [(−3)³]² · (−3)−4 =
10 [(−3)6 : (−3)³]³ · (−3)0 · (−3)−4 =
Realizar las siguientes operaciones con potencias:
Soluciones:
1 (−3)1 · (−3)³ · (−3)4 = (−3)8 = 6561
2 (−27) · (−3) · (−3)² · (−3)0= (−3)³ · (−3) · (−3)² · (−3)0 = (−3)6 = 729
3 (−3)² · (−3)³ · (−3)−4 = −3
4 3−2 · 3−4 · 34 = 3−2 = 1/3² = 1/9
5 5² : 5³ = 5−1 = 1/5
6 5−2 : 5³ = 5−5 = 1/55 = 1/3125
7 5² : 5−3 = 55 = 3125
8 5−2 : 5−3 = 5
9 (−3)1 · [(−3)³]² · (−3)−4 = (−3)1 · (−3)6· (−3)−4 = (−3)³
Primero calculamos la potencia de una potencia y después multiplicamos
10 [(−3)6 : (−3)³]³ · (−3)0 · (−3)−4 = [(−3)³]³ · (−3)0· (−3)−4 = (−3)9 · (−3)0 · (−3)−4 = (−3)5 =−243
En primer lugar hacemos la división indicada en el corchete, después realizamos la potencia de una potencia y por último multiplicamos las potencias
Si buscas clases particulares matematicas Barcelona, Superprof es tu lugar.













Apuntes es una plataforma dirigida al estudio y la práctica de las matemáticas a través de la teoría y ejercicios interactivos que ponemos a vuestra disposición. Esta información está disponible para todo aquel/aquella que quiera profundizar en el aprendizaje de esta ciencia. Será un placer ayudaros en caso de que tengáis dudas frente algún problema, sin embargo, no realizamos un ejercicio que nos presentéis de 0 sin que hayáis si quiera intentado resolverlo. Ánimo, todo esfuerzo tiene su recompensa.
Respuestas.
(-3)+(-3 ) +(-3)+(-3)+(-3)
5*3 15
Deberían poner las respuestas
Para saber si el procedimiento que realizamos es correcto
Por lo general las ponemos y con explicación, no se a qué artículo te refieras y si puedes mencionarlo para corregirlo.
Una pregunta que se tiene en 0+7?
Necesito ayuda para 5ejemplos relacionados con números enteros y su respectiva solucion
Es menor porque todos saben que los números enteros positivos simpre pero siempre seran mayores que cualquier otro número negativo
es mayor
30 es majur que 25