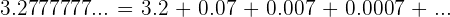Chapters
- Exercise 1
- Exercise 2
- Exercise 3
- Exercise 4
- Exercise 5
- Exercise 6
- Exercise 7
- Exercise 8
- Exercise 9
- Solution of exercise 1
- Solution of exercise 2
- Solution of exercise 3
- Solution of exercise 4
- Solution of exercise 5
- Solution of exercise 6
- Solution of exercise 7
- Solution of exercise 8
- Solution of exercise 9

Exercise 1
The second term of a geometric sequence is  , and the fifth term is
, and the fifth term is  . Determine the sequence.
. Determine the sequence.
Exercise 2
The 1st term of a geometric sequence is  and the eighth term is
and the eighth term is 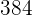 . Find the common ratio, the sum, and the product of the first
. Find the common ratio, the sum, and the product of the first  terms.
terms.
Exercise 3
Compute the sum of the first  terms of the sequence:
terms of the sequence: 
Exercise 4
Calculate the sum of the terms of the following geometric sequence:

Exercise 5
Calculate the product of the first 5 terms of the sequence: 
Exercise 6
John has purchased  books. The 1st book costs 1 dollar, the 2nd, 2 dollars, the 3rd, 4 dollars, and the 4th, 8 dollars, and so on. How much did John pay for the 20 books?
books. The 1st book costs 1 dollar, the 2nd, 2 dollars, the 3rd, 4 dollars, and the 4th, 8 dollars, and so on. How much did John pay for the 20 books?
Exercise 7
The sides of a square, l, have lines drawn between them connecting adjoining sides with their midpoints. This creates another square within the original and this process is continued indefinitely. Calculate the sum of the areas of the infinite squares.
Exercise 8
Calculate the fraction that is equivalent to 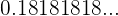
Exercise 9
Calculate the fraction that is equivalent to 
Solution of exercise 1
The second term of a geometric sequence is  , and the fifth term is
, and the fifth term is  . Determine the sequence.
. Determine the sequence.

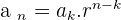
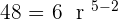
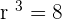

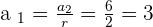
3, 6, 12, 24, 48, ...
Solution of exercise 2
The 1st term of a geometric sequence is  and the eighth term is
and the eighth term is 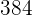 . Find the common ratio, the sum, and the product of the first
. Find the common ratio, the sum, and the product of the first  terms.
terms.


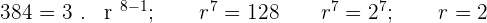


Solution of exercise 3
Compute the sum of the first 5 terms of the sequence: 

Solution of exercise 4
Calculate the sum of the terms of the following geometric sequence:

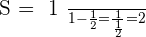
Solution of exercise 5
Calculate the product of the first 5 terms of the sequence: 

Solution of exercise 6
John has purchased  books. The 1st book costs 1 dollar, the 2nd, 2 dollars, the 3rd, 4 dollars, and the 4th, 8 dollars, and so on. How much did John pay for the 20 books?
books. The 1st book costs 1 dollar, the 2nd, 2 dollars, the 3rd, 4 dollars, and the 4th, 8 dollars, and so on. How much did John pay for the 20 books?


 dollars
dollars
Solution of exercise 7
The sides of a square, l, have lines drawn between them connecting adjoining sides with their midpoints. This creates another square within the original and this process is continued indefinitely. Calculate the sum of the areas of the infinite squares.
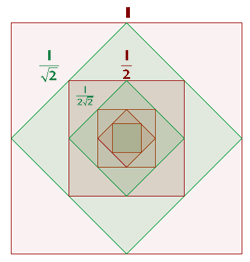
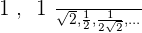


Solution of exercise 8
Calculate the fraction that is equivalent to 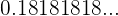
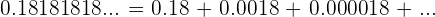
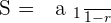

Solution of exercise 9
Calculate the fraction that is equivalent to