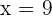Chapters

Exercise 1
The fourth term of an arithmetic sequence is  and the sixth term is
and the sixth term is  . Determine the sequence.
. Determine the sequence.
Exercise 2
The first term of an arithmetic sequence is  and the fifteenth term is
and the fifteenth term is  . Find the common difference and the sum of the first fifteen terms.
. Find the common difference and the sum of the first fifteen terms.
Exercise 3
Find the sum of the first fifteen multiples of  .
.
Exercise 4
Find the sum of the first fifteen numbers ending in 5.
5.
Exercise 5
Find the sum of the first fifteen even numbers greater than  .
.
Exercise 6
Find the angles of a convex quadrilateral, knowing they are in arithmetic sequence and  .
.
Exercise 7
The lower leg of a right triangle is  cm in length. Calculate the other two knowing that the sides of the triangle form an arithmetic sequence.
cm in length. Calculate the other two knowing that the sides of the triangle form an arithmetic sequence.
Exercise 8
Calculate three numbers in an arithmetic sequence, whose sum is  and the sum of their squares is
and the sum of their squares is  .
.
Solution of exercise 1
The fourth term of an arithmetic sequence is  and the sixth term is
and the sixth term is  . Determine the sequence.
. Determine the sequence.



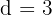


Sequence = 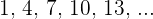
Solution of exercise 2
The first term of an arithmetic sequence is  and the fifteenth term is
and the fifteenth term is  . Find the common difference and the sum of the first fifteen terms.
. Find the common difference and the sum of the first fifteen terms.







Solution of exercise 3
Find the sum of the first fifteen multiples of  .
.







Solution of exercise 4
Find the sum of the first fifteen numbers ending in  .
.







Solution of exercise 5
Find the sum of the first fifteen even numbers greater than  .
.







Solution of exercise 6
Find the angles of a convex quadrilateral, knowing they are in arithmetic sequence and  .
.
The sum of the interior angles of a quadrilateral is 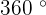 .
.





Hence,

Solution of exercise 7
The lower leg of a right triangle is 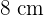 in length. Calculate the other two knowing that the sides of the triangle form an arithmetic sequence.
in length. Calculate the other two knowing that the sides of the triangle form an arithmetic sequence.





 is rejected because length is always positive.
is rejected because length is always positive.

Solution of exercise 8
Calculate three numbers in an arithmetic sequence, whose sum is  and the sum of their squares is
and the sum of their squares is  .
.
Central term x