In this article, we will discuss how to evaluate a given function if its limit approaches to infinity and we get an indeterminate form of zero times infinity or infinity times zero. But before proceeding to discuss that, first, we will see what are limits and l'Hôpital's Rule because both these concepts are closely related to our main topic.
What are Limits?
Limits are used to represent how a function performs when its independent variable, x, is close to a specific number. The formal definition of a limit is given below:
Suppose f is a function defined on a specific open interval that has a number a, except at a itself. We can conclude that the limit of f(x) as x approaches to a is L, and we can write it in mathematical notation like this:
\lim_ {x\rightarrow a} f(x) = L
Suppose for every number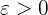 
, there is a corresponding number 
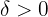in such as way that:
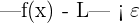
whenever:
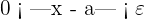
l'Hôpital's Rule
Suppose f and g are differentiable functions, with g'(x) not equal to zero in an interval around a, except a itself. In such a case, one of the following must be true:
- Both the functions f(x) and g(x) have limit zero as x approaches a
- Both the functions f(x) and g(x) have infinite limit (either positive or negative) as x approaches a
Then, the limit of the ratio of f and g, i.e.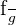 
is equal to the limit of the ratio of f ' and g ', i.e., 
{where the prime represents the appropriate derivative}, until the limit exists, or is infinite.
l'Hôpital's Rule can be applied in one of the following forms of the limit:
, where both f(x) and g(x) approach to 0- , where both f(x) and g(x) approach to infinity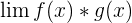
, where f(x) approaches to infinity and g(x) approaches to 0
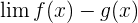, where both f(x) and g(x) approach infinity
, where both f(x) and g(x) approach to 0- , where f(x) approaches to infinity and g(x) approaches to 0
- , where f(x) approaches 1 and g(x) approaches infinity
In this article, we will discuss how to apply l'Hôpital's Rule if 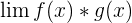, where f(x) approaches to infinity and g(x) approaches to 0. Therefore, we can call it zero times infinity or infinity times zero.
In the next section, we will solve a couple of examples step by step which will explain how to apply the above discussed rule when both the functions are multiplied with each other and limit approaches to infinity.
Example 1
Evaluate \lim_ {x \rightarrow \infty} (x^2 sin \frac{1}{x^2})
Solution
The above function has an indeterminate form of 
because \lim_ {x \rightarrow \infty}(x^2) is equal to 
, and \lim_ {x \rightarrow \infty} \frac{1}{x^2} is equal to 0.
The function 
can be written as:
When we will apply the limit on the above function as shown below, we will still get an indeterminate form of 
or 
:
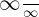\lim _ {x \rightarrow \infty} \frac {sin \frac{1}{x^2}} {\frac{1}{x^2}}
As, the function still has an indeterminate form, hence we will apply l'Hôpital's Rule here. To apply the l'Hôpital's Rule, we will take the first derivative of numerator and denominator separately. The first derivative of 
is 
and the derivative of 
is 
. Now, substitute these derivatives in the function like this:
= \lim _ {x \rightarrow \infty} \frac {cos (\frac{1}{x^2}) \cdot (-\frac{2}{x^3})} {-\frac{2}{x^3}}
Simplifying the above expression will give us the following result:
= \lim _ {x \rightarrow \infty} cos \frac{1}{x^2}
When we will apply limit on the above function we will get the following answer:
= 
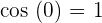
Example 2
Evaluate \lim_ {x \rightarrow \infty} (3x tan \frac{1}{x})
Solution
The above function has an indeterminate form of because \lim_ {x \rightarrow \infty}(3x) is equal to , and \lim_ {x \rightarrow \infty} \frac{1}{x} is equal to 0.
The function 
can be written as:
When we will apply the limit on the above function as shown below, we will still get an indeterminate form of or :
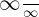\lim _ {x \rightarrow \infty} \frac {tan \frac{1}{x}} {\frac{1}{3x}}
As, the function still has an indeterminate form, hence we will apply l'Hôpital's Rule here. To apply the l'Hôpital's Rule, we will take the first derivative of numerator and denominator separately. The first derivative of 
is 
and the derivative of 
is 
. Now, substitute these derivatives in the function like this:
= \lim _ {x \rightarrow \infty} \frac {-sec^2 (\frac{1}{x}) \cdot (-\frac{1}{x^2})} {-\frac{1}{3x^2}}
Simplifying the above expression will give us the following result:
= \lim _ {x \rightarrow \infty} \frac {-sec^2 (\frac{1}{x})} {- \frac{1}{3}}
When we will apply limit on the above function we will get the following answer:
= 
= 
Example 3
Evaluate \lim_ {x \rightarrow \infty} (x + 6) \frac{1}{x^2 + 3}
Solution
The above function has an indeterminate form of 
because \lim_ {x \rightarrow \infty}(x + 6) is equal to , and \lim_ {x \rightarrow \infty} x^2 + 3 is also equal to \infty.
The function 
can be written as:
When we will apply the limit on the above function as shown below, we will still get an indeterminate form of :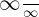
= \lim _ {x \rightarrow \infty} \frac {x + 6} {x^2 + 3}
As, the function still has an indeterminate form, hence we will apply l'Hôpital's Rule here. To apply the l'Hôpital's Rule, we will take the first derivative of numerator and denominator separately. The first derivative of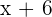 
is 
and the derivative of 
is 2x. Now, substitute these derivatives in the function like this:
= \lim _ {x \rightarrow \infty} \frac {1}{2x}
Applying the limit on the above function will give us the following result:
= 
= 
Example 4
Evaluate \lim_ {x \rightarrow \infty} (x + 15) \frac{1}{x^2 + 6x + 36}
Solution
The above function has an indeterminate form of because \lim_ {x \rightarrow \infty}(x + 15) is equal to , and \lim_ {x \rightarrow \infty} x^2 + 6x + 36 is also equal to \infty.
The function 
can be written as:
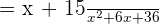
When we will apply the limit on the above function as shown below, we will still get an indeterminate form of :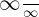
\lim _ {x \rightarrow \infty} \frac {x + 15} {x^2 + 6x + 36}
As, the function still has an indeterminate form, hence we will apply l'Hôpital's Rule here. To apply the l'Hôpital's Rule, we will take the first derivative of numerator and denominator separately. The first derivative of 
is and the derivative of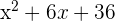 
is 2x + 6. Now, substitute these derivatives in the function like this:
= \lim _ {x \rightarrow \infty} \frac {1}{2x + 6}
Applying the limit on the above function will give us the following result:
=
=
Did you like this article? Rate it!
Loading...
Correct equals infinity equals 16 but not true. It’s it’s six it’s infinity.
And this, my friends, is why humans will be conquered by AI… so many logic holes it’s… well, infinite. lol
Is 0^infinity ( zero to the power infinity) indeterminate form? How?
Didn’t Cantor proved that there are a group of infinities (the Aleph zero & Aleph one sets, for example)? And these are grouped around the concept of infinite to the power infinity, if I remember correctly .
Exercise 3
I think it is discontinuous at 0
exercise 2 : the function is not defined for x= 0.
exercise 1 q 5 The function has a jump discontinuity at x = 1, should be x=0.