Chapters
In this article, we will learn how to calculate the limits of a logarithmic function in detail.
There are two primary properties of limits that are used while computing the limits of the logarithmic functions. The standard results which we get from these properties can be employed as formulas in calculus for dealing with the functions which involve the logarithmic functions. These two properties are discussed here in detail:
1) The limit of the quotient of the natural logarithm of 1 + x divided by x is equal to 1. Mathematically, we can write it as:
\lim_{x \rightarrow 0} \frac {log_e (1 +x)} {x} = 1
2) If we have the ratio of the logarithm of 1 + x to the base x, then it is equal to the reciprocal of natural logarithm of the base.
\lim_{x \rightarrow 0} \frac {log_b (1 +x)} {x} = \frac {1} {log_e b}
Now, we will learn how to evaluate the problems involving the limit of the logarithmic function.
Example 1
Evaluate \lim _ {x \rightarrow 0} \frac {ln (sin x)} {\sqrt [3] {1 + 2x} - 1}
Solution
In the first step, we will substitute x = 0 in the above function as shown below:
=\lim _ {x \rightarrow 0} \frac {ln (sin (0))} {\sqrt [3] {1 + 2(0)} - 1}
According to the trigonometry, the value of sine zero is equal to one:
=\lim _ {x \rightarrow 0} \frac {ln (1)} {\sqrt [3] {1 + 0} - 1}
Solve the remaining function arithmetically as shown below:
=\lim _ {x \rightarrow 0} \frac {0} {\sqrt [3] {1 } - 1}
=\lim _ {x \rightarrow 0} \frac {0} {0}
The result of the function in this example is an indeterminate form.
Example 2
Evaluate \lim _ {x \rightarrow 0} \frac {tan x + 2} {ln (\sqrt {1})}
Solution
In the first step, we will substitute x = 0 in the above function as shown below:
=\lim _ {x \rightarrow 0} \frac {tan (0) + 2} {ln (\sqrt {1})}
According to the trigonometry, the value of tangent zero is equal to zero:
=\lim _ {x \rightarrow 0} \frac {0 + 2} {ln (\sqrt{1}}
Solve the remaining function arithmetically as shown below:
=\lim _ {x \rightarrow 0} \frac {2} {ln (1)}
=\lim _ {x \rightarrow 0} \frac {2} {0}
The result of the function in this example is indeterminate form because 0 is in the denominator.
Example 3
Evaluate \lim _{x \rightarrow e} \frac{ln (x) - 2} {x - 2e}
Solution
Here, we will employ L'Hôpital's rule which says that if we have the function of the form 
which meet any of the following two conditions:
- Both the functions in the numerator and the denominator f(x) and g(x) have a of limit zero as x approaches a
- Both the functions in the ratio f(x) and g(x) have infinite limit positive or negative) as x approaches a
Then, the limit of the ratio of f and g, i.e.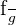 
is equal to the limit of the ratio of derivatives of f and g , i.e., 
, until the limit exists, or is infinite.
Using this rule, we need to find the derivative of the numerator and the denominator like this:
=\lim _{x \rightarrow e} \frac{\frac{1}{x} - 0} {1 - 0}
=\lim _{x \rightarrow e} \frac{1}{x}
Now, we will substitute x in the above function with e as shown below:
=\frac{1} {e}
Example 4
Evaluate \lim _ {x \rightarrow 1} \frac {log(x)}{2x - 2}
Solution
When we substitute 1 directly in the above expression we get the indeterminate form of 
. Therefore, we will apply L'Hôpital's rule here. To use this rule, we need to take the derivative of the functions in the numerator and the denominator as shown below:
= \lim _ {x \rightarrow 1} \frac {\frac{1}{x}}{2 - 0}
= \lim _ {x \rightarrow 1} \frac {\frac{1}{x}}{2}
Now, we will substitute x with 1 in the above expression to get the final answer as shown below:
= \lim _ {x \rightarrow 0} \frac {\frac{1}{1}}{2}
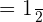
Example 5
Evaluate \lim _ {x \rightarrow 3} \frac {log(x - 2)}{3x - 9}
Solution
When we substitute 3 directly in the above expression we get the indeterminate form . Therefore, we will apply L'Hôpital's rule here. To use this rule, we need to take the derivative of the functions in the numerator and the denominator as shown below:
= \lim _ {x \rightarrow 3} \frac {\frac{1}{x - 2}}{3 - 0}
= \lim _ {x \rightarrow 3} \frac {\frac{1}{x - 2}}{3}
Now, we will substitute x with 3 in the above expression to get the final answer as shown below:
= \lim _ {x \rightarrow 0} \frac {\frac{1}{1}}{3}
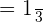
Example 6
Evaluate \lim _ {x \rightarrow 0} \frac {cos x + 1} {log (\sqrt {4})}
Solution
In the first step, we will substitute x = 0 in the above function as shown below:
=\lim _ {x \rightarrow 0} \frac {cos (0) + 1} {log (\sqrt {4})}
According to the trigonometry, the value of cosine zero is equal to one:
=\lim _ {x \rightarrow 0} \frac {1 + 1} {log (\sqrt{4}}
Solve the remaining function arithmetically as shown below:
=\lim _ {x \rightarrow 0} \frac {2} {log (2)}
=\lim _ {x \rightarrow 0} \frac {2} {0.301}
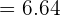
Example 7
Evaluate \lim _ {x \rightarrow 0} \frac {(tan x + sin x) + 3} {log (\sqrt {9})}
Solution
In the first step, we will substitute x = 0 in the above function as shown below:
\lim _ {x \rightarrow 0} \frac {(tan (0) + sin (0)) + 3} {log (\sqrt {9})}
According to the trigonometry, the values of sin and tangent zero are equal to one:
=\lim _ {x \rightarrow 0} \frac {0 + 0 + 3} {log (\sqrt{9}}
Solve the remaining function arithmetically as shown below:
=\lim _ {x \rightarrow 0} \frac {3} {log (3)}
=\lim _ {x \rightarrow 0} \frac {3} {0.301}
Example 8
Evaluate \lim _ {x \rightarrow 0} \frac {log x} {2sin x + 5}
Solution
In the first step, we will substitute x = 0 in the above function as shown below:
\lim _ {x \rightarrow 0} \frac {log (0)} {2sin (0) + 5}
According to the trigonometry, the value of sine zero is equal to one:
=\lim _ {x \rightarrow 0} \frac {log (0)} {5}
Solve the remaining function arithmetically as shown below:
=\lim _ {x \rightarrow 0} \frac {-\infty} {5}
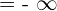
Example 9
Evaluate \lim _ {x \rightarrow 1} \frac {log (2x -2)} {8x + 3}
Solution
In the first step, we will substitute x = 1 in the above function as shown below:
\lim _ {x \rightarrow 1} \frac {log (2(1) -2)} {8(1) + 3}
According to the trigonometry, the value of sine zero is equal to one:
=\lim _ {x \rightarrow 0} \frac {log (0)} {11}
Solve the remaining function arithmetically as shown below:
=\lim _ {x \rightarrow 0} \frac {-\infty} {11}
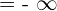
Example 10
Evaluate \lim _ {x \rightarrow 0} \frac {cos x + 2} {log (\sqrt {9})}
Solution
In the first step, we will substitute x = 0 in the above function as shown below:
=\lim _ {x \rightarrow 0} \frac {cos (0) + 2} {log (\sqrt {9})}
According to the trigonometry, the value of cosine zero is equal to one:
=\lim _ {x \rightarrow 0} \frac {1 + 2} {log (\sqrt{9}}
Solve the remaining function arithmetically as shown below:
=\lim _ {x \rightarrow 0} \frac {3} {log (3)}
=\lim _ {x \rightarrow 0} \frac {3} {0.477}
Example 11
Evaluate \lim _ {x \rightarrow 0} \frac {cos x + tan x - 8 } {log (\sqrt {25})}
Solution
In the first step, we will substitute x = 0 in the above function as shown below:
=\lim _ {x \rightarrow 0} \frac {cos (0) + tan (0) - 8} {log (\sqrt {25})}
According to the trigonometry, the value of cosine zero is 1 and tangent zero is zero:
=\lim _ {x \rightarrow 0} \frac {-7} {log (\sqrt{25}}
Solve the remaining function arithmetically as shown below:
=\lim _ {x \rightarrow 0} \frac {-7} {log (5)}
=\lim _ {x \rightarrow 0} \frac {-7} {0.698}
Did you like this article? Rate it!
Loading...
Correct equals infinity equals 16 but not true. It’s it’s six it’s infinity.
∞ = -1/12
By Sriniwas aramanujan
And this, my friends, is why humans will be conquered by AI… so many logic holes it’s… well, infinite. lol
Is 0^infinity ( zero to the power infinity) indeterminate form? How?
Didn’t Cantor proved that there are a group of infinities (the Aleph zero & Aleph one sets, for example)? And these are grouped around the concept of infinite to the power infinity, if I remember correctly .
Exercise 3
I think it is discontinuous at 0
exercise 2 : the function is not defined for x= 0.
exercise 1 q 5 The function has a jump discontinuity at x = 1, should be x=0.