What is Intermediate Value Theorem
Let's say you checked the continuity of the function of closed intervals and you found that the function is continuous. That is not all, you also need to check whether the function passes through the expected points. We call that expected point an Intermediate Value. For example, a function proves to be continuous on ending points, "a" and "b". A point, "c", is somewhere between both points. If the graph is continuous, it should pass through point "c" as well. To prove that, we use a theorem which is called the Intermediate Value Theorem. This theorem says, "If a function is continuous on the closed interval 
and k is any number between 
and 
then there exists a number, c, within 
such that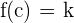 
."
By observing the graph, the intermediate value theorem can be defined another way:
- If a function is continuous on the closed interval , the function takes all values between and in this interval.
- The intermediate value theorem does not indicate the value or values of c, it only determines their existence.
You must be wondering why the intermediate value theorem is important? Because it provides valuable data. This theorem can help in the evaluation of the function at a specific point. Furthermore, it can be used to prove the existence of the roots of an equation.
Example
Prove that the image of 
exists in function 
.
The function is continuous in 
as it is the product of two continuous functions.
Take the interval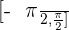 
, and study the value of the extremes:
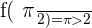
Therefore there is a 
such that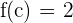 
.
Prove that the image of 
exists in function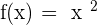 
with intervals 
.
The function is continuous in as it is the product of two continuous functions.
Studying extreme values:
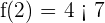
Therefore there is a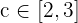 
such that 
.
Did you like this article? Rate it!
Loading...
Correct equals infinity equals 16 but not true. It’s it’s six it’s infinity.
∞ = -1/12
By Sriniwas aramanujan
And this, my friends, is why humans will be conquered by AI… so many logic holes it’s… well, infinite. lol
Is 0^infinity ( zero to the power infinity) indeterminate form? How?
Didn’t Cantor proved that there are a group of infinities (the Aleph zero & Aleph one sets, for example)? And these are grouped around the concept of infinite to the power infinity, if I remember correctly .
Exercise 3
I think it is discontinuous at 0
exercise 2 : the function is not defined for x= 0.
exercise 1 q 5 The function has a jump discontinuity at x = 1, should be x=0.