Whether the function is continuous or not is also important data. Functions can be distinguished on the basis of continuity. Polynomial, rational, radical, exponential, logarithmic and trigonometric functions are continuous at all points of their domain. So, what is a continuous function? Keep on reading to find out.
Continuous Function
Take a pencil and graph paper and draw a line. Start from one end and finish it to the opposite end without lifting the pencil. You will see a proper line without any breaks in between. We will call the function continuous. There is only one condition for a continuous function and that is there should be not a single breakpoint. It should be like a graph drawn without lifting the pencil from the graph. If there is some kind of breakpoint, it won't be a continuous function.
Of course, that line will have an equation. Let's say the equation is 
. Below is the graph of .
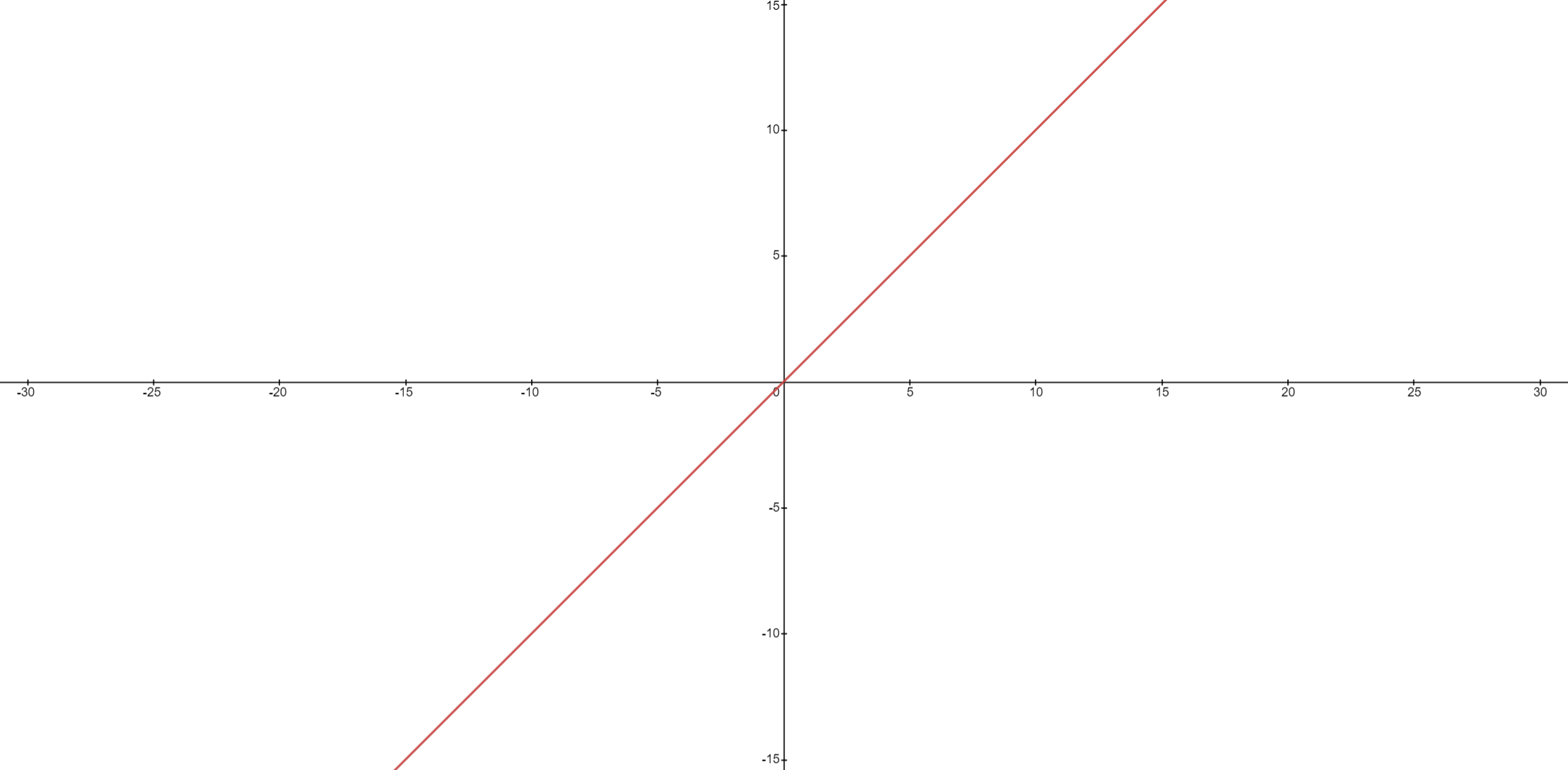
Let's gather some data, we know at when x is equal to 15, y will also be equal to 15. When x is equal to 2, y is also equal to 2. The graph is plotted from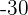 
to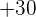 
for abscissa and 
to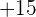 
for ordinate. However, you want to find what will be the value of y when x is equal to 
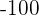? Do you need to draw the graph again? No, you can predict the value, the value of y will be 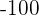because the function is continuous. This example shows that we can make predictions of higher values if the function is continuous. What if there is a breakpoint in the graph?
Discontinuity
Suppose you have a function, 
. Let's plot it on the graph.
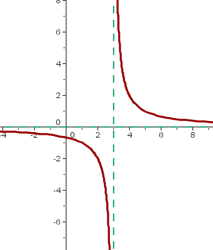
At 
, we see that the function is going to infinity from both sides. It seems that the pencil is lifted up to draw the second curve. Both lines don't meet each other and there is a gap between them. We call them discontinuous function. There are many types of discontinuous functions, they are:
- Jump discontinuity
- Point discontinuity
- Infinite discontinuity
These types of discontinuous are in detail and deserve their own resource which we will talk about later. In the case of the graph, the function is continuous 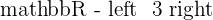at 
. At it is not continuous because the function does not exist at this point.
Piecewise Functions
In the above example, we talked about a single equation that is defined by a function, i.e. 
. Normally, a function doesn't have a single equation, it might be defined by multiple equations within a single function with their ranges. We call them piecewise function. Piecewise functions are continuous if every function is in its interval of definition, and if the functions match their side limits at the points of separation of their intervals. For example, we have a function,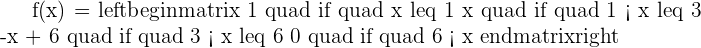 
. Let's plot it and check what comes up.
Although there are multiple equations within a function, however, their ranges are coinciding in a way that the pencil was not lifted while plotting this graph. In conclusion, the function 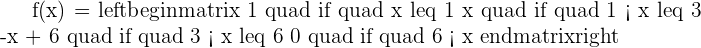is continuous at 
, because its constituent functions are polynomial and the side limits at the points of division coincide. Please do note that not all piecewise functions are continuous. They can be continuous and they can be discontinuous. Since we are talking about continuity, we made this example to show how piecewise function can be continuous.
In Nutshell
If f and g are continuous at 
, then:
is continuous at .
is continuous at .
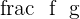is continuous at , if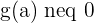 
.
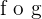is continuous at .
Did you like this article? Rate it!
Loading...
Correct equals infinity equals 16 but not true. It’s it’s six it’s infinity.
And this, my friends, is why humans will be conquered by AI… so many logic holes it’s… well, infinite. lol
Is 0^infinity ( zero to the power infinity) indeterminate form? How?
Didn’t Cantor proved that there are a group of infinities (the Aleph zero & Aleph one sets, for example)? And these are grouped around the concept of infinite to the power infinity, if I remember correctly .
Exercise 3
I think it is discontinuous at 0
exercise 2 : the function is not defined for x= 0.
exercise 1 q 5 The function has a jump discontinuity at x = 1, should be x=0.