Chapters
- Exercise 1
- Exercise 2
- Exercise 3
- Exercise 4
- Exercise 5
- Exercise 6
- Exercise 7
- Exercise 8
- Exercise 9
- Solution of exercise 1
- Solution of exercise 2
- Solution of exercise 3
- Solution of exercise 4
- Solution of exercise 5
- Solution of exercise 6
- Solution of exercise 7
- Solution of exercise 8
- Solution of exercise 9

Exercise 1
Find the point(s) of discontinuity for the function 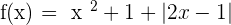 .
.
Exercise 2
Consider the function:
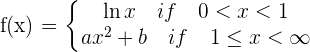
If 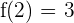 , determine the values of a and b for which f(x) is continuous.
, determine the values of a and b for which f(x) is continuous.
Exercise 3
Given the function:
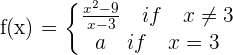
Determine the value of a for which the function is continuous at  .
.
Exercise 4
Given the function:
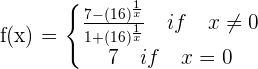
Determine the points of discontinuity.
Exercise 5
Given the function:
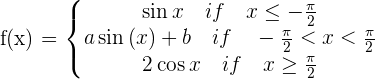
Determine a and b so that the function  is continuous for all values of x.
is continuous for all values of x.
Exercise 6
Given the function:

Determining the value of a for which f(x) is continuous.
Exercise 7
Calculate the value of k for the following continuous function.
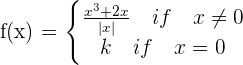
Exercise 8
Given the function:

Determine the values for a and b in order to create a continuous function.
Exercise 9
Determine the values for a and b in order to create a continuous function.
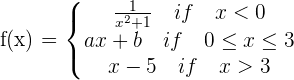
Solution of exercise 1
Find the point(s) of discontinuity for the function 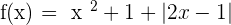 .
.

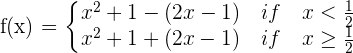



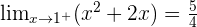
There are no points of discontinuity as the function is continuous.
Solution of exercise 2
Consider the function:
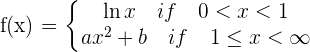
If 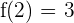 , determine the values of a and b for which f(x) is continuous.
, determine the values of a and b for which f(x) is continuous.
There is only a question of continuity at  .
.
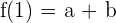
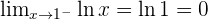
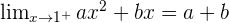
For the function to be continuous:
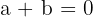
On the other hand there is:

Solve the system of equations and obtain:

Solution of exercise 3
Given the function:
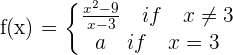
Determine the value of a for which the function is continuous at  .
.
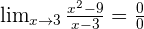

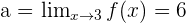
Solution of exercise 4
Given the function:
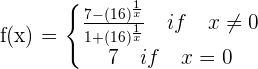
Determine the points of discontinuity.
The exponential function is positive for all  , therefore the denominator of the function cannot be annulled.
, therefore the denominator of the function cannot be annulled.
There is only doubt of the continuity at  .
.
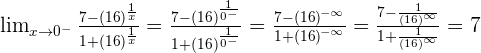

Solve the indeterminate form dividing by 
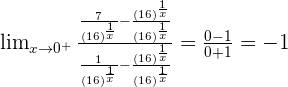
The function is continuous on  .
.
See also in trigonometric working demo.
Solution of exercise 5
Given the function:
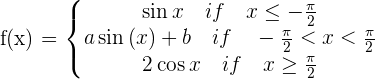
Determine a and b so that the function  is continuous for all values of x.
is continuous for all values of x.

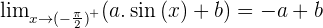
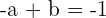
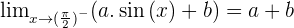

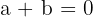

Solution of exercise 6
Given the function:

Determining the value of a for which f(x) is continuous.
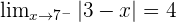
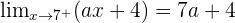

Solution of exercise 7
Calculate the value of k for the following continuous function.
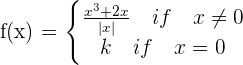
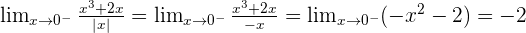
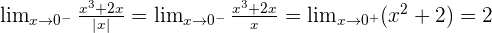
Therefore there is no limit for the function and there is no value that would make f(x) continuous at  , regardless of what value k is given.
, regardless of what value k is given.
Solution of exercise 8
Given the function:
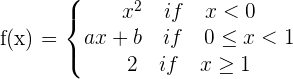
Determine the values for a and b in order to create a continuous function.

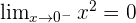
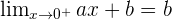
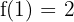
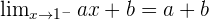

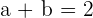

Solution of exercise 9
Determine the values for a and b in order to create a continuous function.
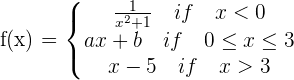
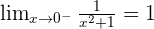
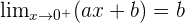

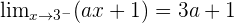
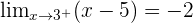














Correct equals infinity equals 16 but not true. It’s it’s six it’s infinity.
∞ = -1/12
By Sriniwas aramanujan
And this, my friends, is why humans will be conquered by AI… so many logic holes it’s… well, infinite. lol
Is 0^infinity ( zero to the power infinity) indeterminate form? How?
Didn’t Cantor proved that there are a group of infinities (the Aleph zero & Aleph one sets, for example)? And these are grouped around the concept of infinite to the power infinity, if I remember correctly .
Exercise 3
I think it is discontinuous at 0
exercise 2 : the function is not defined for x= 0.
exercise 1 q 5 The function has a jump discontinuity at x = 1, should be x=0.