Balzano's Theorem
A particular case of the intermediate value theorem is Bolzano's theorem. This theorem proposes that if a function is continuous on a closed interval, 
and 
and 
have opposite sign then there is at least one value of x for which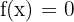 
. Usually, that value of x is denoted with "c" in many textbooks.
Bolzano's theorem does not indicate the value or values of c, it only confirms their existence. Let's prove this theorem.
Bolzano's Theorem Proof
Imagine a continuous function where point a is the minimum point and point b is the maximum point, 
and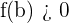 
. Now we will divide the interval into two equal parts and call the mid point c, therefore, there will be two intervals, 
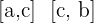. There are three possibilities in this scenario and they are:
If the first condition occurs then you already proved this theorem's existence. On the other hand, the last two possibilities have some contradictions. Let's say that 
, since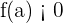 
, we will consider the 
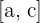interval. If 
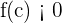then we will consider the 
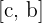interval where 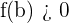. In both conditions, there is one term a negative entity while the other term is a positive entity.
Now we will select a sub-interval such that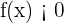 
at its negative end points and 
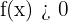at its positive end points. We will denote this sub-interval by 
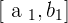where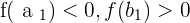 
.
The next step is to bisect the close intervals into two equal parts as shown above. This can either result in 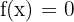or new sub-interval which we will name 
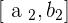. Where 
, now we will again bisect the sub-interval.
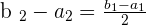
Since, , therefore:
This is following a sequence which is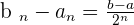 
. This process can go till infinity. Thus we get a sequence of nested intervals.
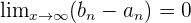
Example
Verify that the equation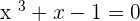 
has at least one real solution in the interval 
.
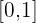We consider the function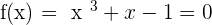 
, which is continuous on 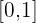because it is polynomial. We study the sign in the extremes of the interval:
First, consider the function 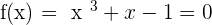, which is continuous in 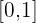because it is polynomial. Then, study the sign in the extremes of the interval:
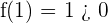
As the signs are different, Bolzano's theorem can be applied which determines that there is a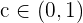 
such that 
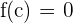. This process demonstrates that there is a solution in this interval.
Did you like this article? Rate it!
Loading...
Correct equals infinity equals 16 but not true. It’s it’s six it’s infinity.
And this, my friends, is why humans will be conquered by AI… so many logic holes it’s… well, infinite. lol
Is 0^infinity ( zero to the power infinity) indeterminate form? How?
Didn’t Cantor proved that there are a group of infinities (the Aleph zero & Aleph one sets, for example)? And these are grouped around the concept of infinite to the power infinity, if I remember correctly .
Exercise 3
I think it is discontinuous at 0
exercise 2 : the function is not defined for x= 0.
exercise 1 q 5 The function has a jump discontinuity at x = 1, should be x=0.