Rolle's theorem is a special case of Mean Value Theorem. Both mean value theorem and Rolle's theorem are important concepts of calculus. In this article, we will discuss what is Rolle's theorem in detail along with the relevant examples.

Rolle's Theorem
"If a function is continuous on the closed interval [a, b] and differentiable on (a, b) and f(a) = f(b), then, there exists a point, c which is an element of (a, b) such that f'(c) = 0"
The definition shows that the function should only be continuous, but also a differentiable function on the interval (a, b).
The graphical interpretation of Rolle's Theorem states that there is a point where the tangent is parallel to the x-axis as shown in the graph below:
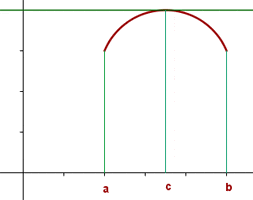
All the following three conditions must be satisfied for the Rolle's theorem to be true:
- f(x) should be continuous on a closed interval [a, b]
- The derivative of f(x) should exist on an open interval (a, b)
- f(a) should be equal to f(b)
The physical interpretation of the Rolle's theorem is straightforward. Consider an object moving in a straight line. After some time, the object moves backwards to reach the starting point. During this time, a moment comes when the instantaneous velocity of an object is zero.
In the next section, we will solve some examples related to Rolle's theorem.
Example 1
Suppose  . Find all values of c in the interval [-2, 0] in such a way that
. Find all values of c in the interval [-2, 0] in such a way that 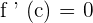 .
.
Solution
In the first step, we need to verify if the above function f(x) fulfills all the conditions of Rolle's theorem:
a) Since f(x) is a quadratic function, therefore it is continuous at the interval [-2, 0].
b) It can also be differentiated on the open interval (-2, 0)
c) We can check whether f(a) = f(b) by substituting -2 and 0 in the function like this:

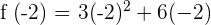


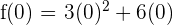
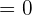
Hence, f(a) = f(b). This shows that the function satisfies all the three conditions of Rolle's theorem.
For computing the point c, we need to find the first-derivative of the function using sum/difference and power rules like this:


Substitute x with c:
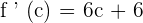
According to Rolle's theorem, 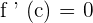 :
:

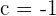
Hence, for 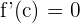 , the value of c is equal to -1.
, the value of c is equal to -1.
Example 2
Suppose 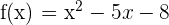 . Find all values of c in the interval [-1, 6] in such a way that
. Find all values of c in the interval [-1, 6] in such a way that 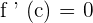 .
.
Solution
In the first step, we need to verify if the above function f(x) fulfills all the conditions of Rolle's theorem:
a) Since f(x) is a quadratic function, therefore it is continuous at the interval [-1, 6].
b) It can also be differentiated on the open interval (-1, 6)
c) We can check whether f(a) = f(b) by substituting -1 and 6 in the function like this:
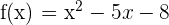
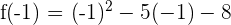
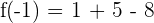
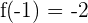
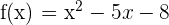

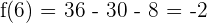
Hence, f(a) = f(b). This shows that the function satisfies all the three conditions of Rolle's theorem.
To compute the point c, we need to find the derivative of the function using sum/difference and power rules like this:
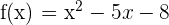

Substitute x with c:
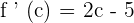
According to Rolle's theorem, 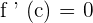 :
:
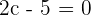
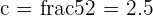
Hence, for 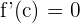 , the value of c is equal to 2.5.
, the value of c is equal to 2.5.
Example 3
Suppose 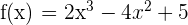 . Find all values of c in the interval [2, 0] in such a way that
. Find all values of c in the interval [2, 0] in such a way that 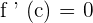 .
.
Solution
In the first step, we need to verify if the above function f(x) fulfills all the conditions of Rolle's theorem:
a) Since f(x) is a quadratic function, therefore it is continuous at the interval [2, 0].
b) It can also be differentiated on the open interval (2, 0)
c) We can check whether f(a) = f(b) by substituting 2 and 0 in the function like this:
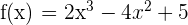
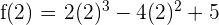

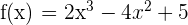
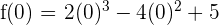
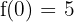
Hence, f(a) = f(b). This shows that the function satisfies all the three conditions of Rolle's theorem.
For computing the point c, we need to find the derivative of the function using sum/difference and power rules like this:
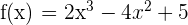

Substitute x with c:

According to Rolle's theorem, 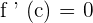 :
:

The above equation is a quadratic equation of the form  . Here, a = 6, b = 8 and the last constant is equal to 0. We will use the following quadratic formula to find the values of c:
. Here, a = 6, b = 8 and the last constant is equal to 0. We will use the following quadratic formula to find the values of c:

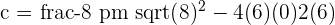
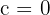 and
and 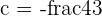
We will discard the negative value 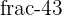 because it is not the part of the closed interval [2,0]. Hence, the only value of c is 0.
because it is not the part of the closed interval [2,0]. Hence, the only value of c is 0.
Example 4
Suppose 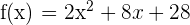 . Find all values of c in the interval [-3, -1] in such a way that
. Find all values of c in the interval [-3, -1] in such a way that 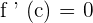 .
.
Solution
In the first step, we need to verify if the above function f(x) fulfills all the conditions of Rolle's theorem:
a) Since f(x) is a quadratic function, therefore it is continuous at the interval [-3, -1].
b) It can also be differentiated on the open interval (-3, -1)
c) We can check whether f(a) = f(b) by substituting -3 and -1 in the function like this:
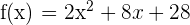

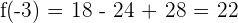
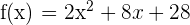
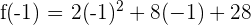
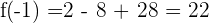
Hence, f(a) = f(b). This shows that the function satisfies all the three conditions of Rolle's theorem.
For computing the point c, we need to find the derivative of the function using sum/difference and power rules like this:
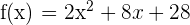
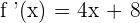
Substitute x with c:
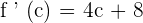
According to Rolle's theorem, 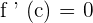 :
:
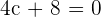

Hence, for 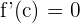 , the value of c is equal to -2.
, the value of c is equal to -2.
Example 5
Given the interval [a,b], the function  satisfies the Rolle's theorem. If the known value of a is 0, find the value of b.
satisfies the Rolle's theorem. If the known value of a is 0, find the value of b.
Solution
It is given that the function satisfies the Rolle's theorem over an interval [a, b]. It means that it is continuous over this interval and differentiable over an open interval (a, b). It also satisfies the condition  . We only need to find out the value of b.
. We only need to find out the value of b.
To find the value of b, we will find the roots of the above function:

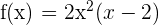
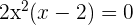
It is evident that the function has two roots. One is 0 and the other is 2. Hence, the value of b is 2.
Example 6
Suppose 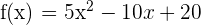 . Find all values of c in the interval [0, 2] in such a way that
. Find all values of c in the interval [0, 2] in such a way that 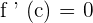 .
.
Solution
In the first step, we need to verify if the above function f(x) fulfills all the conditions of Rolle's theorem:
a) Since f(x) is a quadratic function, therefore it is continuous at the interval [0, 2].
b) It can also be differentiated on the open interval (0, 2)
c) We can check whether f(a) = f(b) by substituting 0 and 2 in the function like this:
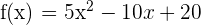

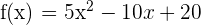
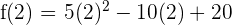
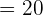
Hence, f(a) = f(b). This shows that the function satisfies all the three conditions of Rolle's theorem.
For computing the point c, we need to find the derivative of the function using sum/difference and power rules like this:
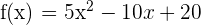

Substitute x with c:
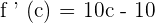
According to Rolle's theorem, 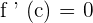 :
:

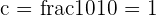
Hence, for 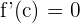 , the value of c is equal to 1.
, the value of c is equal to 1.













