Chapters
In this article, we will discuss what is a definite integral, its properties, and how to use the properties of a definite integral to solve problems. So, let us get started.

Introduction
The definite integral of the function has a close relationship with the indefinite integral and antiderivative of a function. The main difference lies in the fact that if the indefinite integral of the function exists, then it is a real number value. A definite integral has start and end values. It means that there is a closed interval [a, b].
The integral notation was first proposed by Gottfried Wilhelm Leibniz in the seventeenth century. He discovered calculus along with Isaac Newton. The integration symbol  is a stretched form of S, which suggests summation or sigma. There are boundaries of the interval [a, b] above and below the integration symbol in a definite interval. These numbers a and b represent the x- values. They are also known as limits of integration. The lower limit is represented by a, and the lower limit is denoted by b.
is a stretched form of S, which suggests summation or sigma. There are boundaries of the interval [a, b] above and below the integration symbol in a definite interval. These numbers a and b represent the x- values. They are also known as limits of integration. The lower limit is represented by a, and the lower limit is denoted by b.
The integral symbol in the definition of definite integral looks similar to the indefinite integral symbol to denote the antiderivative of a function. Although the symbols to represent definite and indefinite integrals of the functions seem alike, however, both the concepts are different from one another. A definite integral is a number, whereas, an indefinite integral is a group of functions.
In the next section, we have will discuss the formal definition of a definite integral and how to write it in mathematical notation.
Definite Integral
Given a function, f(x), and a closed interval [a, b], the definite integral represents the area bounded by the graph of f(x), the x-axis and the vertical lines x = a and x = b.

The definite integral is denoted by  , where:
, where:
∫ is the sign of integration.
a is the lower limit of integration.
b is the upper limit of integration.
f(x) is the integrand.
dx is the differential of x, and indicates the variable of the function to be integrated.
Properties of the Definite Integral
Some of the properties of definite integrals will be explained in this section.
Reverse Interval
The sign of the value of the definite integral changes when the limits of integration are interchanged. Mathematically, this property can be written as:
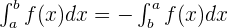
Zero-Length Interval
The definite integral is zero if the integration limits are the same. Mathematically, we can denote this property like this:
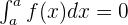
Adding Intervals
If c is a point inside the closed interval [a, b], then we break down the definite integral as a sum of two integrals in the closed intervals [a, c] and [c, b]. Mathematically, we can write this property like this:
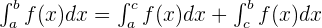
Sum/Difference
The definite integral of the sum or difference of the functions is equal to the sum or difference of integrals. Mathematically, we can write it as:
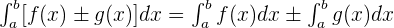
Constant Multiple
The integral of the constant multiplied by a function is equal to the product of the constant and the integral of the function. Mathematically, we can write it as:
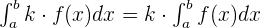
In the next section, we will solve some examples using the above discussed properties of definite integrals.
Example 1
If 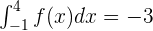 and
and 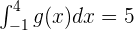 , then find
, then find 
Solution
Write the function  using the sum/difference property of definite integrals like this:
using the sum/difference property of definite integrals like this:
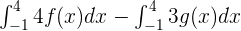
Now, we will use the constant multiple property of definite integral to write the function like this:
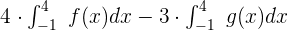
Now, in this step, we will plug in the values 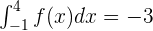 and
and 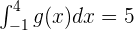 in the above function like this:
in the above function like this:
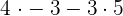
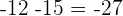
Example 2
If  and
and  , then find
, then find 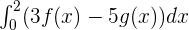
Solution
Write the function 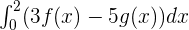 using the sum/difference property of definite integrals like this:
using the sum/difference property of definite integrals like this:

Now, we will use the constant multiple property of definite integral to write the function like this:
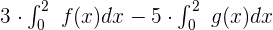
Now, in this step, we will plug in the values  and
and  in the above function like this:
in the above function like this:
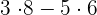
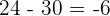
Example 3
Using the result of the 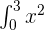 , find
, find 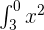 .
.
Solution
First, we need to find the antiderivative of the function 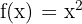 . The antiderivative of this function is
. The antiderivative of this function is  . Consider C = 0 for the ease of calculation.
. Consider C = 0 for the ease of calculation.
According to the fundamental theorem of calculus:

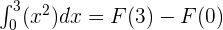
Substitute 3 and 0 in the antiderivative of the function:


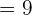
Now, we have calculated the value of 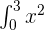 . To calculate
. To calculate  , we will use reverse interval property. According to the reverse property of definite interval, the sign of the value of the definite integral changes when the limits of integration are interchanged. Hence,
, we will use reverse interval property. According to the reverse property of definite interval, the sign of the value of the definite integral changes when the limits of integration are interchanged. Hence,
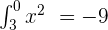
Example 4
Find 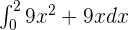 using the properties of definite integral.
using the properties of definite integral.
Solution
First, factor 9 out of both the terms and write the function like this:
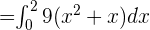
Now, we will use the constant multiple property of definite integral which says that the integral of the constant multiplied by a function is equal to the product of the constant and the integral of the function.
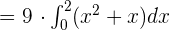
Now, find the antiderivative of the function 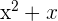 . The antiderivative is
. The antiderivative is  . For your ease, consider C = 0.
. For your ease, consider C = 0.
According to the fundamental theorem of calculus:


Substitute 2 and 0 in the antiderivative of the function:



Hence, the result of the function  is
is  . But, we have to find
. But, we have to find  . So, we will simply multiply 9 with
. So, we will simply multiply 9 with  to get the final answer:
to get the final answer:

Example 5
Find  .
.
Solution
We will use the adding intervals property of definite integral to write the above function like this:

Now, to calculate the definite integral, we will first find the antiderivative of the function. The antidertivatve of the function is 5x.
According to the fundamental theorem of calculus:

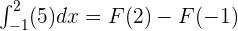
Substitute 2 and -1 in the antiderivative of the function: