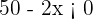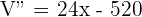Chapters
Exercise 1
Determine the sides of the largest isosceles triangle that can fit within a circle with a radius of 
.
Exercise 2
An isosceles triangle with a perimeter of 
turns about the vertical axis generating a three-dimensional cone. What should the length of the base be in order to maximize the volume of the resultant cone?
Exercise 3
A manufacturer seeks to produce a cylindrical can (complete with a lid) with a capacity of one litre. What should the dimensions of the can be in order to minimize the amount of metal used?
Exercise 4
Decompose the number 
into two summands such that five times the square of the first summand over six times the square of the second summand is the minimum possible resultant.
Exercise 5
A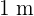 
long piece of wire needs to be divided into two pieces that will form a circle and a square. Determine the length of each piece so that the sum of the areas of the circle and square is minimized.
Exercise 6
Find the dimensions of the largest possible rectangle that can be drawn in an isosceles triangle whose base is 
and height,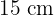 
.
Exercise 7
The surface area cost of construction per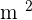 
for a large box is 50 dollars for the base, 60 dollars for the top and 40 dollars for the walls. Find the dimensions of this box that minimize the cost if its volume has to be 9 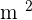and its height, .
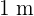Exercise 8
Cutting squares out of each corner of a sheet of cardboard creates a box without a lid. If the cardboard sheet has dimensions of 
, determine the size of each equally sized square to be removed from the cardboard sheets (see figure) in order to maximize the volume of the resultant box.
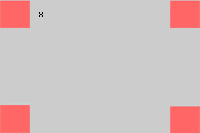
Solution of exercise 1
Determine the sides of the largest isosceles triangle that can fit within a circle with a radius of .
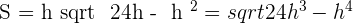
Differentiating:
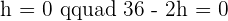
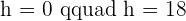
BASE: 
SIDE: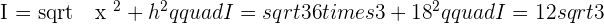 
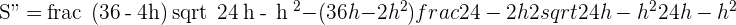
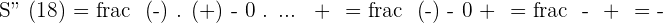
Solution of exercise 2
An isosceles triangle with a perimeter of turns about the vertical axis generating a three-dimensional cone. What should the length of the base be in order to maximize the volume of the resultant cone?
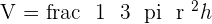
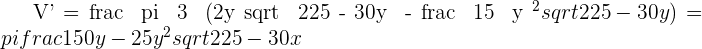
BASE: 
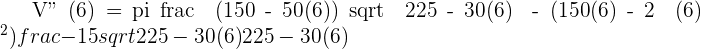
Solution of exercise 3
A manufacturer seeks to produce a cylindrical can (complete with a lid) with a capacity of one litre. What should the dimensions of the can be in order to minimize the amount of metal used?
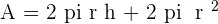
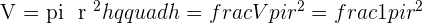
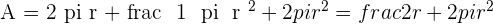
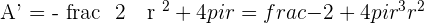
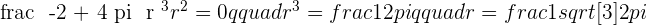
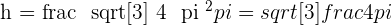
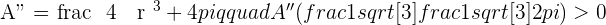
Solution of exercise 4
Decompose the number into two summands such that five times the square of the first summand over six times the square of the second summand is the minimum possible resultant.
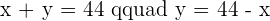
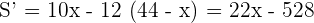
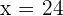
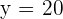
Solution of exercise 5
A 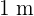long piece of wire needs to be divided into two pieces that will form a circle and a square. Determine the length of each piece so that the sum of the areas of the circle and square is minimized.
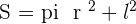
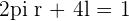
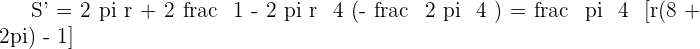
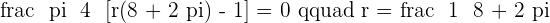
Circle = 
Square = 
Solution of exercise 6
Find the dimensions of the largest possible rectangle that can be drawn in an isosceles triangle whose base is and height, .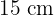
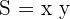
By having two similar triangles it's true that:
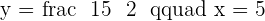
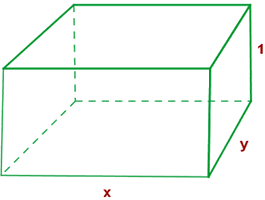
Solution of exercise 7
The surface area cost of construction per 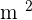for a large box is 50 dollars for the base, 60 dollars for the top and 40 dollars for the walls. Find the dimensions of this box that minimize the cost if its volume has to be 9 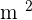and its height, .
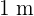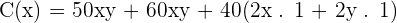
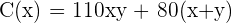
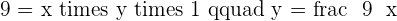
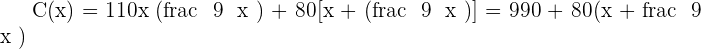
Solution of exercise 8
Cutting squares out of each corner of a sheet of cardboard creates a box without a lid. If the cardboard sheet has dimensions of , determine the size of each equally sized square to be removed from the cardboard sheets (see figure) in order to maximize the volume of the resultant box.
We will negate the value of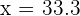 
because when we place it in 
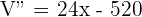, it won't fulfil this condition 
Did you like this article? Rate it!
Loading...
