Chapters
- Exercise 1
- Exercise 2
- Exercise 3
- Exercise 4
- Exercise 5
- Exercise 6
- Exercise 7
- Exercise 8
- Exercise 9
- Exercise 10
- Exercise 11
- Exercise 12
- Solution of exercise 1
- Solution of exercise 2
- Solution of exercise 3
- Solution of exercise 4
- Solution of exercise 5
- Solution of exercise 6
- Solution of exercise 7
- Solution of exercise 8
- Solution of exercise 9
- Solution of exercise 10
- Solution of exercise 11
- Solution of exercise 12

Exercise 1
Calculate the points where the tangent to the curve y = x³ − 3x² − 9x + 5 is parallel to the x-axis.
Exercise 2
A tangent with a slope of 3 and which passes through the point (0, −2) has been drawn on the curve y= x³. Find the point of contact between the function and the tangent.
Exercise 3
Find the points on the curve f(x) = x4 + 7x³ + 13x² + x + 1, for which the tangent makes an angle of 45° with the x-axis.
Exercise 4
Given the function f(x) = tan x, find the angle between the tangent line at the origin of f(x) with the horizontal axis.
Exercise 5
Calculate the equation of the tangent and normal lines for the curve f(x) = ln tan 2x, at the point where the x-coordinate is: x = π/8.
Exercise 6
Find the coefficients of the equation y = ax² + bx + c, knowing that its graph passes through (0, 3) and (2, 1), and at the second point, its tangent has a slope of 3.
Exercise 7
The graph of the function y = ax² + bx + c passes through the points (2, 3) and (3, 13) and the tangent to the curve with an x-coordinate of 1 is parallel to the bisector of the first quadrant. Find the numerical value of a, b and c.
Exercise 8
Given the function f(x) = ax³ + bx² + cx + d. Determine the value of a, b, c and d knowing that the curve passes through points (−1, 2) (2, 3), and that the tangents at the points on the curve with x-coordinates of 1 and −2 are parallel to the x-axis.
Exercise 9
At what point of the curve y = ln x, is its tangent parallel to the line that joins the points (1, 0) and (e, 1)?
Exercise 10
Determine the values of b, for which the tangents to the curve of the function f(x) = b²x³ + bx² + 3x + 9 at x = 1 and x = 2 are parallel.
Exercise 11
Given the equation 9x²+ y² = 18, find the equation of the tangent line that is parallel to the line of equation 3x − y + 7 = 0.
Exercise 12
Find the area of the triangle determined by the coordinate axes and the tangent to the curve xy = 1 at x = 1.
Solution of exercise 1
Calculate the points where the tangent to the curve y = x³ − 3x² − 9x + 5 is parallel to the x-axis.
y' = 3x² − 6x − 9; x² − 2x − 3 = 0 (simplifying for 3)
x1 = 3 y1 = −22
x2 = −1y2 = 10
A(3, −22) B(−1, 10)
Solution of exercise 2
A tangent with a slope of 3 and which passes through the point (0, −2) has been drawn on the curve y= x³. Find the point of contact between the function and the tangent.
Point of contact: (a, f(a)).
f'(x)= 3x²f'(a)= 3a²
3a²= 3a = ±1
The equations of the tangent lines are:
a = 1 f(a) = 1
y − 1 = 3(x − 1) y = 3x − 2
a = −1 f(a) = −1
y + 1 = 3(x + 1) y = 3x + 2
The point (0, −2) belongs to the straight line y = 3x − 2.
So, the point of tangency is (1, 1) .
Solution of exercise 3
Find the points on the curve f(x) = x4 + 7x³ + 13x² + x + 1, for which the tangent makes an angle of 45° with the x-axis.
m = 1
f'(x) = 4x³ + 21x² + 26x + 1
4x³ + 21x² + 26x + 1 = 1
x = 0 x = −2 x = 13/4
P(0, 4) Q(−2, 4) R(13/4, 1621/256)
Solution of exercise 4
Given the function f(x) = tan x, find the angle between the tangent line at the origin of f(x) with the horizontal axis.
f′(x) = 1 + tan² x f′(0) = 1 = m
y = x
α = arc tan 1 = 45º
Solution of exercise 5
Calculate the equation of the tangent and normal lines for the curve f(x) = ln tan 2x, at the point where the x-coordinate is: x = π/8.

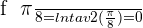
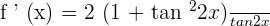

Equation of the tangent:
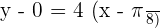
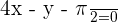
Equation of the normal:
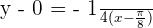

Solution of exercise 6
Find the coefficients of the equation y = ax² + bx + c, knowing that its graph passes through (0, 3) and (2, 1), and at the second point, its tangent has a slope of 3.
(0, 3) 3 = c
(2, 1) 1= 4a + 2b + c
y' = 2ax + b 3 = 4a + b
Solving the system:
a = 2 b = −5 c = 3
Solution of exercise 7
The graph of the function y = ax² + bx + c passes through the points (2, 3) and (3, 13). The tangent to the curve with an x-coordinate of 1 is parallel to the bisector of the first quadrant. Find the numerical value of a, b and c.
(2, 3) 3 = 4a + 2b + c
(3, 13)13 = 9a + 3b +c
y' = 2ax + b 1 = 2a + b
Solve the system:
a = 3 b = −5 c =1
Solution of exercise 8
Given the function f(x) = ax³ + bx² + cx + d. Determine the value of a, b, c and d knowing that the curve passes through points (−1, 2) (2, 3), and that the tangents at the points on the curve with x-coordinates of 1 and −2 are parallel to the x-axis.
f(−1) = 2 −a + b − c + d = 2
f(2) = 3 8a + 4b + 2c + d = 3
f′(−1) = 0 3a + 2b + c = 0
f′(2) = 0 12a − 4b + c = 0
a = − 2/9 b = − 1/3 c = 4/3 d = 31/9
Solution of exercise 9
At what point of the curve y = ln x, is its tangent parallel to the line that joins the points (1, 0) and (e, 1)?
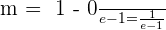
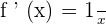
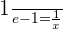
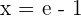
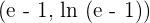
Solution of exercise 10
Determine the values of b, for which the tangents to the curve of the function f(x) = b²x³ + bx² + 3x + 9 at x = 1 and x = 2 are parallel.
For both tangent lines to be parallel, the derivatives at x = 1 and x = 2 must be equal.
f'(1) = f'(2)
f'(x) = 3b²x² + 2bx + 3
f'(1) = 3b² + 2b + 3
f'(2) = 12b² + 4b + 3
3b² + 2b + 3 = 12b² + 4b + 3
9b² + 2b = 0
b = 0 b = −2/9
Solution of exercise 11
Given the equation 9x²+ y²= 18, find the equation of the tangent line that is parallel to the line of equation 3x − y + 7 = 0.
Point of contact: (a, b)
y = 3x + 7 m = 3
After implicitly differentiating there is:


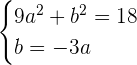

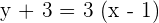
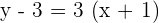
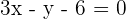
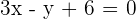
Solution of exercise 12
Find the area of the triangle determined by the coordinate axes and the tangent to the curve xy = 1 at x = 1.

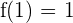

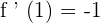

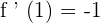

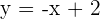


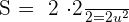
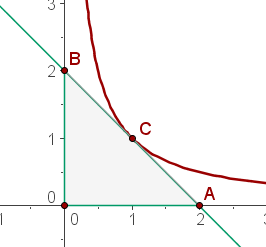













Like the explanation, want to rearn more. Really enjoying the documents received.