Chapters
Integers behave differently on powers. Sometimes, the answer will result in positive while in other cases, it can result in negative. This is a bit complex but once you understand how integers work with different powers and this why in this lesson you will learn how to find the result of an integer which has power. Another word for power is exponent so if you read exponent somewhere then don't get worried, it means the same. So, what does the exponent represents? Exponents mean how many times a number is multiplied by itself. For example, if you see 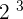 , this means you need to multiply
, this means you need to multiply  by itself and there will be 3 terms. It will be like this
by itself and there will be 3 terms. It will be like this  . If there was no concept of exponents, our calculation could have gone very long and there would be a high probability that someone would have made an error in it.
. If there was no concept of exponents, our calculation could have gone very long and there would be a high probability that someone would have made an error in it.
The power of a natural exponent of an integer is another integer. The absolute value of the result is the absolute value of the base multiplied by itself as specified by the exponent. In simple words, the absolute value multiples itself according to the power but what about the sign? Will it also change? The answer is yes and here is the complexity. The sign also changes according to the power but how to find that? Don't worry, it can be determined by the following rule:
Rule No.1
The powers of an even exponent are always positive. It means that even if the integer has a negative sign, it will always result in a positive number.
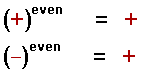
For example:
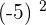


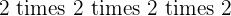

Rule No.2
The powers of an odd exponent have the same sign as the base. In simple words, all you need to do is to multiply the number according to its power and add the same sign that was mentioned in the question.
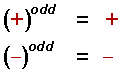
For example:
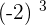
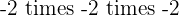

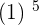
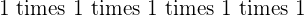


Properties
Like every other mathematical operations, powered integers also have some properties.
Property No.1: Zero Power
If you raised any number's power to zero, it will always result in 1. It doesn't matter whether the number is an integer or any other number, it will always be equal to 1.
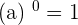
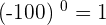
Property No.2: Standard Power of Any Number
Every number has power. If you see a number that doesn't mention a power that means it has a power of  . Hence, every number has a power of
. Hence, every number has a power of  .
.
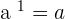
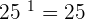
Property No.3: Multiplication of Powers with the Same Base
If there is a multiplication sign and the numbers are the same having different powers then you can add both powers. In other words, it is another power with the same base and the exponent is the sum of the exponents.
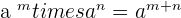

Property No.4: Division of Powers with the Same Base
If there is a division sign and the numbers are the same having different powers then you can subtract both powers. In other words, it is another power with the same base and the exponent is the difference of the exponents.
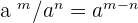
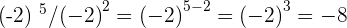
Property No.5: Power of a Power
It is another power with the same base and the exponent is the product of the exponents.


Property No.6: Multiplication of Powers with the Same Exponent
If the bases are different but the power of both bases are the same with a multiplication sign then you can write them in a group and then apply the multiplication operation. In other words, It is another power with the same exponent, whose base is the product of the bases.
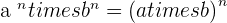
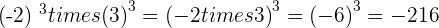
Property No.7: Division of Powers with the Same Exponent
If the bases are different but the power of both bases are the same with a division sign then you can write them in a group and then apply the division operation. It is another power with the same exponent, whose base is the quotient of the bases.

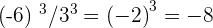
Fractional Exponent, Exponents Worksheets.













