Chapters
- Exercise 1
- Exercise 2
- Exercise 3
- Exercise 4
- Exercise 5
- Exercise 6
- Exercise 7
- Exercise 8
- Exercise 9
- Solution of exercise 1
- Solution of exercise 2
- Solution of exercise 3
- Solution of exercise 4
- Solution of exercise 5
- Solution of exercise 6
- Solution of exercise 7
- Solution of exercise 8
- Solution of exercise 9

Exercise 1
Exercise 2
For the following numbers: 179, 311, 848, 3,566, 7,287, indicate which are prime and which composite numbers.
Exercise 3
Determine, using a table, all the prime numbers between 400 and 450.
Exercise 4
Factor the following numbers:
- 216
- 360
- 432
Exercise 5
Factor 342 and determine its number of divisors.
Exercise 6
Factor the following numbers:
- 2,250
- 428 and 376
- 3,500
- 2,520
Exercise 7
Calculate the greatest common divisor (GCD) and the lowest common multiple (LCM) of the following numbers:
- 148 and 156
- 600 and 1,000
Exercise 8
Calculate the greatest common divisor (GCD) and the lowest common multiple (LCM) of the following numbers:
- 72, 108 and 600
- 1,048, 786 and 3,930
- 3,120, 6,200 and 1,864
Exercise 9
Determine, using the Euclidean algorithm, the greatest common divisor (GCD) of the following:
- 72 and 16
- 656 and 848
- 1,278 and 842
Solution of exercise 1
816, 833, 850
Solution of exercise 2
For the following numbers: 179, 311, 848, 3,566, 7,287, indicate which are prime and which composite numbers.
Prime numbers: 179 and 311 because each has only two multiples, 1 and the number itself.
Composite numbers : 848, 3,566 and 7,287. These numbers have more than two multiples, so we have categorized them as composite numbers.
Solution of exercise 3
Determine, using a table, all the prime numbers between 400 and 450.
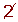 | 401 |  | 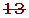 |  | 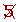 | 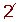 | 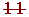 | 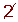 | 409 |
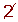 | 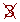 |  |  | 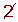 | 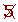 | 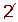 | 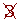 | 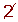 | 419 |
 | 421 | 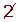 |  | 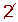 |  | 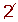 |  | 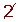 |  |
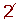 | 431 | 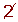 | 433 |  | 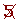 | 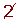 | 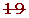 | 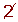 | 439 |
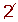 | 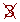 | 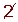 | 443 | 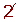 | 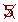 | 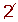 | 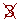 | 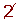 | 449 |
Solution of exercise 4
Factor the following numbers:
- 216
| 2 | 216 |
|---|---|
| 2 | 108 |
| 2 | 54 |
| 3 | 27 |
| 3 | 9 |
| 3 | 3 |
| 1 |
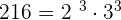
2. 360
| 2 | 360 |
|---|---|
| 2 | 180 |
| 2 | 90 |
| 3 | 45 |
| 3 | 15 |
| 5 | 5 |
| 1 |

3. 432
| 2 | 432 |
|---|---|
| 2 | 216 |
| 2 | 108 |
| 2 | 54 |
| 3 | 27 |
| 3 | 9 |
| 3 | 3 |
| 3 | 1 |

Solution of exercise 5
Factor 342 and determine its number of divisors.

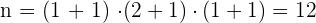
Solution of exercise 6
Factor the following numbers:
- 2,250
| 2 | 2250 |
|---|---|
| 3 | 1125 |
| 3 | 375 |
| 5 | 125 |
| 3 | 21 |
| 7 | 7 |
| 1 |
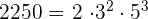
2. 3,500
| 2 | 3500 |
|---|---|
| 2 | 1750 |
| 5 | 875 |
| 5 | 175 |
| 5 | 35 |
| 7 | 7 |
| 1 |
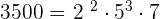
3. 2,520
| 2 | 2520 |
|---|---|
| 2 | 1260 |
| 2 | 630 |
| 3 | 315 |
| 3 | 105 |
| 5 | 35 |
| 7 | 7 |
| 1 |

Solution of exercise 7
Calculate the greatest common divisor (GCD) and the lowest common multiple (LCM) of the following numbers:
1. 428 and 376

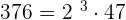
G.C.D. 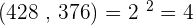
L.C.M. 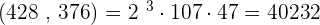
2. 148 and 156
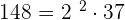
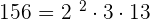
GCD 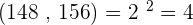
LCM 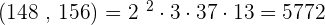
3. 600 and 1,000
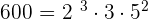
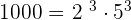
GCD 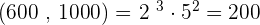
LCM 
Solution of exercise 8
Calculate the greatest common divisor (GCD) and the lowest common multiple (LCM) of the following numbers:
1. 72, 108 and 60.


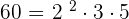
GCD 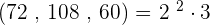
LCM 
| 2 | 1048 |
|---|---|
| 2 | 524 |
| 2 | 262 |
| 131 | 131 |
| 1 |
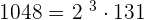
| 2 | 786 |
|---|---|
| 3 | 393 |
| 131 | 131 |
| 1 |
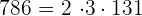
| 2 | 3930 |
|---|---|
| 3 | 1965 |
| 5 | 655 |
| 131 | 131 |
| 1 |
 GCD
GCD  LCM
LCM 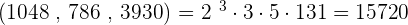
3. 3,120, 6,200 and 1,864
| 2 | 3120 |
|---|---|
| 2 | 1560 |
| 2 | 780 |
| 2 | 390 |
| 5 | 195 |
| 3 | 39 |
| 13 | 13 |
| 1 |
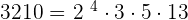
| 2 | 6200 |
|---|---|
| 2 | 3100 |
| 2 | 1550 |
| 5 | 775 |
| 5 | 155 |
| 31 | 31 |
| 1 |
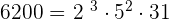
| 2 | 1864 |
|---|---|
| 2 | 932 |
| 2 | 416 |
| 2 | 208 |
| 2 | 104 |
| 2 | 52 |
| 2 | 26 |
| 13 | 13 |
| 1 |

GCD 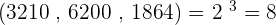
LCM 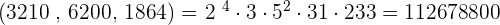
Solution of exercise 9
Determine, using the Euclidean algorithm, the greatest common divisor (GCD) of:
1. 72 and 16

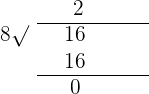
GCD (72, 16) = 8

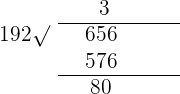


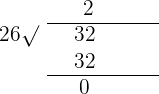
GCD (656, 848) = 16
3. 17,28 and 842
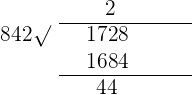

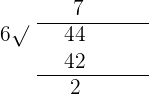

GCD (1,278, 842) = 2













