Chapters
In order to understand divisibility, you need to understand what division means. In simple words, division means to divide two numbers in maths. For example, we have two numbers, they are number a and number b. If we are dividing b by a, it means that we are finding how many a parts are available in the b. That is called division. It is written in this form.
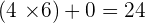
Where 
is the divisor,
is the quotient,
is the remainder,
and 
is the dividend.
However, divisibility is something else. It is derived from division but there is a twist in it. Divisibility says that if two numbers (let's say a and b) are divided, the division should be exact. This means that the remainder should be equal to zero. You might be wondering that this means the above example is also an example of divisibility? The answer is yes! It is also an example of divisibility because if you look carefully, the remainder is zero. The only difference between division and divisibility is that division can give you a remainder and that is fine but not in the case of divisibility because divisibility says the remainder should always be zero.
Rules of Divisibility
There are some rules of divisibility. Although the condition will remain the same (which is the remainder should always be zero), however, when you are finding divisible of different numbers, these rules can come in handy.
Divisible by 2
A number is divisible by 
if its last digit is a zero or an even number.
Divisible by 3
A number is divisible by 
if the sum of its digits is a multiple of .
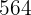
, is multiple
2,040
, is multiple
Divisible by 5
A number is divisible by 
, if it ends in zero or five.
Divisible by 7
A number is divisible by 
when the difference between the number without the figure of the units and the double the number of the units is or a multiple of .
, is multiple of .
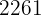
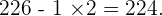
Repeat the process with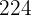 
.
, is multiple of .
Divisible of 11
A number is divisible by 
if the difference between the sum of the figures who occupy the even numbers and the odd numbers is 0 or a multiple of .
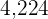
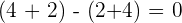
Other rules
Divisible by 4
A number is divisible by if the last two digits are zeros or a multiple of .
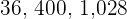
Divisible by 6
A number is divisible by if it is divisible by and .
Divisible by 8
A number is divisible by 
if its last three figures are zeros or a multiple of .
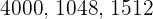
Divisible by 9
A number is divisible by 
if the sum of its digits gives a multiple of .
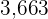
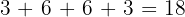, is multiple of
Divisible by 10
A number is divisible by 
if the last figure in the unit is .
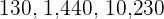
Divisible by 25
A number is divisible by 
if their last two digits are zeros or a multiple of .
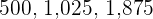
Divisible by 125
A number is divisible by 
if its last three figures are zeros or a multiple of .
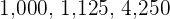
Factoring
Factoring a number into prime factors is to express the number as a product of prime numbers.
Find more Maths tutor near me here on Superprof.
Did you like this article? Rate it!
Loading...
